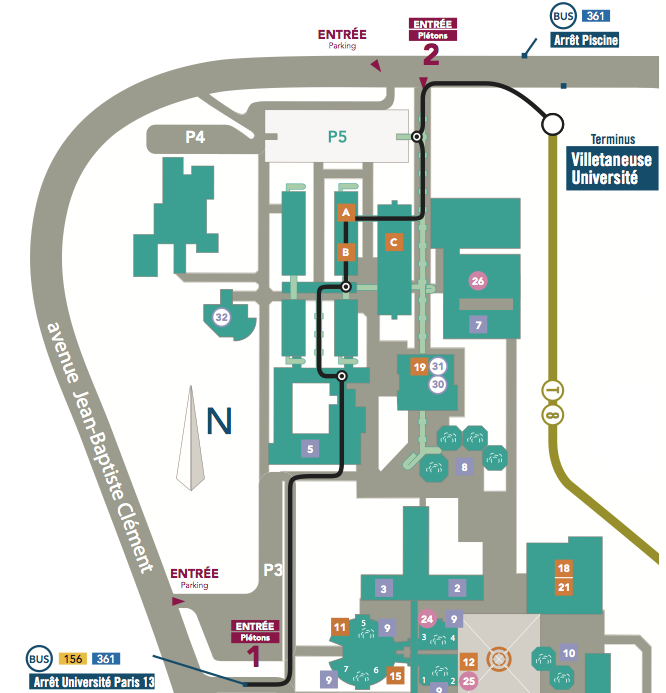
Si vous souhaitez venir donner un exposé chez nous, ce serait avec grand plaisir, n'hésitez pas à contacter le responsable du créneau correspondant !
24/02/2026
Germain Poullot Construisons le cône sous-modulaire par récurrenceabstract.htmlCette présentation plonge, en particulier, dans l'article
https://arxiv.org/abs/2510.03177 avec Georg Loho et Arnau Padrol. Nous commencerons par une (longue) introduction aux déformations de polytopes.
Un permutoèdre déformé (aussi appelé permutoèdre généralisé, ou fonction sous-modulaire) est un polytope dont toutes les arêtes ont pour direction $e_i - e_j$ pour certains $i \neq j$. L'ensemble des permutoèdres déformés vivant dans $\mathbb R^n$ forme un cône, le cône sous-modulaire. Nous proposons une construction "inductive" du cône sous-modulaire, en utilisant une opération nommée GP-sum : à partir de deux permutoèdres déformés dans $\mathbb R^n$, nous créons (bijectivement) un permutoèdre déformé dans $\mathbb R^{n+1}$.
Munis de cette construction, nous créons de nouveaux rayons du cône sous-modulaire, c'est-à-dire de nouveaux permutoèdres déformés indécomposables (au sens de la somme de Minkowski). Cela nous permet d'améliorer les bornes connues sur le nombre de rayons du cône sous-modulaire, notamment en produisant $2^{2^n}$ rayons. Plus encore, nous étudions le f-vecteur du cône sous-modulaire, son nombre total de faces, et le nombre de ses faces simplicial, grâce à la nouvelle partition que cette construction inductive nous donne.
] [article ] 17/02/2026
Vincent Jugé Trier des tableaux partiellement pré-triésabstract.htmlMême si trier une permutation aléatoire requiert n log(n)
comparaisons en moyenne, il existe de nombreux cas d'usage où les
tableaux que l'on souhaite trier ne sont pas des permutations
aléatoires : soit ils contiennent de longues plages contiguës déjà
triées, soit ils contiennent peu de valeurs distinctes. L'algorithme
TimSort, utilisé en Java pour trier des tableaux d'objets composites,
a été conçu spécifiquement pour être plus efficace sur de tels
tableaux pré-triés. Nous découvrirons comment cet algorithme et ses
variantes fonctionnent et pourquoi ils sont efficaces.
] 10/02/2026
Sarah Wajsbrot Hitting affine families of polyhedra, with applications to robust optimizationabstract.htmlGeometric hitting set problems, in which we seek a smallest set of
points that collectively hit a given set of ranges, are ubiquitous in
computational geometry. Most often, the set is discrete and is given
explicitly. We propose new variants of these problems, dealing with
continuous families of convex polyhedra, and show that they capture
decision versions of the two-level finite adaptability problem in
robust optimization. We show that these problems can be solved in
strongly polynomial time when the size of the hitting/covering set and
the dimension of the polyhedra and the parameter space are constant.
We also show that the hitting set problem can be solved in strongly
quadratic time for one-parameter families of convex polyhedra in
constant dimension. This leads to new tractability results for finite
adaptability that are the first ones with so-called left-hand-side
uncertainty, where the underlying problem is non-linear.
Joint work with Jean Cardinal and Xavier Goaoc.
Manuscript:
https://arxiv.org/abs/2504.16642 ] [article ] 03/02/2026
Journées Combinatoires de Bordeaux (2-4 février 2026)27/01/2026
Meltem Ünel
On exponentially height-penalised random treesabstract.htmlÉtant donné $n \in \mathbb{N}$ et $\mu \in \mathbb{R}$, un arbre de taille $n$ biaisé par la hauteur est un arbre planaire aléatoire $T_n$ à $n$ sommets dont la loi est donnée par $P(T_n = t ) \propto e^{−\mu h(t)}$, où $t$ est un arbre fixe à $n$ sommets, et $h(t)$ est la hauteur de $t$ .
Dans cet exposé on va présenter quelques statistiques de ces arbres quand $\mu=\mu(n)$ est une suite à termes positifs dépendant de $n$: la limite d’échelle quand $\mu(n) \sim 1/ \sqrt{n}$, la hauteur ainsi que le comportement autour de la racine quand $0 \leq \mu(n) \ll n$.
L’exposé est basé sur arXiv:2512.17747 en commun avec L. Addario-Berry, B. Corsini et N. Maitra.
] 20/01/2026
Pierre Bonnet Lattice walks with large steps in the first quadrant : algebraicity of the stretched Gessel modelsabstract.htmlLattice walks confined in the first quadrant have been subject to an extended study for about a decade, showing a great variety of techniques to handle functional equations with catalytic variables. A work of Pierre Bonnet and Charlotte Hardouin of 2024 extended those tools in the context of the study of walks based upon models with arbitrarily large steps, allowing to effectively conduct a strategy devised by Bousquet-Mélou, Olivier Bernardi and Kilian Raschel of 2016, providing the algebraicity proofs of some models. In this talk, I show how these tools show the algebraicity of an infinite family of models of walks derived from the Gessel models.
] 16/12/2025
Mercedes Rosas On the enumeration of records of rooted trees and rooted forests [Slides.pdf ]abstract.htmlA record of a rooted Cayley tree is a node whose label is the largest along the unique path to the root. In this work, we find elegant functional equations relating the generating functions for records of rooted Cayley trees and for records of forests of rooted trees with the Cayley tree function, and explore the consequences of our results. This is join work with Adrián Lillo and Stefan Trandafir.
] 09/12/2025
Andrea Sportiello Spanning trees in the assignment problem: two theorems and a conjectureabstract.htmlThe "Minimum Matching Problem" consists in finding an independent edge
set of minimum weight M*(G) in a given edge-weighted undirected graph
G. If G is bipartite, we deal with the "Assignment Problem". We
consider a version of the problem in which we take the union of the
optimal matchings for various slightly-modified versions of the base
graph: H_J(G)=Union_{U in J} M*(G_U).
In this talk we will provide two families of theorems: (1) we prove
that, in two distinct settings for the Assignment Problem, the graphs
H_J, as well as certain associated graphs H'_J, are in fact spanning
trees on the pertinent base graphs G and G'; (2) in the two settings
above, if the weights of the graph edges are given by the p-th power
of the Euclidean distance for points configurations on the plane, the
tree H_J is non-crossing (that is, its natural embedding in the plane
has no crossing edges) when p=1, and (more surprisingly) the
associated tree H'_J is non-crossing when p=2.
Our main motivation for investigating theorems of this form comes from
(a family of) conjectures in Statistical Mechanics, that we will
illustrate in future work: in the Random Euclidean Assignment Problem
(i.e., when the points are chosen i.i.d. on a domain of the plane),
for p=2, the two settings above give trees H'_J which are
asymptotically distributed as the Uniform Spanning Tree with free and
wired boundary conditions, in the two cases. In particular, suitable
paths on the tree in the second setting are asymptotically distributed
as a SLE at kappa=2.
Work in collaboration with Sergio Caracciolo and Gabriele Sicuro
] 02/12/2025
Alice Cousaert
Equiprojective polytopes in high dimension [Slides.pdf ]abstract.htmlA 3-dimensional polytope (the convex hull of finitely many points) is said to be k-equiprojective if almost every planar projections is a k-gon where k is a fixed integer. Two characterisations were established respectively in 2008 by Masud Hasan and Anna Lubiw and in 2024 by Théophile Buffière and Lionel Pournin in the 3-dimensional case.
I will present you a way to generalise the definition of equiprojectivity to d-dimensional polytopes, as well as the tools I built in order to generalise the two different characterisations.
] 25/11/2025
Martino Borello La géométrie des codes linéaires et des applications récentesabstract.htmlIl est bien connu qu’un code linéaire non dégénéré de longueur n et de dimension k peut être associé à un ensemble de n points (avec multiplicités) dans un espace projectif de dimension k−1. Certaines propriétés des codes peuvent être interprétées géométriquement. Cette perspective relie les codes MDS aux problèmes impliquant des arcs dans les espaces projectifs (la fameuse conjecture MDS a été initialement formulée comme un problème de géométrie projective par Segre), les problèmes de recouvrement aux ensembles saturants, les codes minimaux aux ensembles bloquants forts, etc. Dans cette présentation, nous illustrerons certains résultats récents obtenus en utilisant cette approche géométrique pour les codes en métrique de Hamming et nous esquisserons à la fin comment cela peut être généralisé à d’autres métriques, telles que les métriques rang et somme-rang.
] 18/11/2025
Denys Bulavka Algebraic shifting and area rigidity of surfacesabstract.htmlAlgebraic shifting, introduced by Kalai in the 80's, is an operator that canonically associates a shifted complex to a given simplicial complex. The advantage of this operator is that it preserves many combinatorial, topological and algebraic properties of the starting complex and in doing so it translates the initial problem to a simpler instance. We show that among such properties is that of area rigidity, a generalization of graph rigidity, and that every triangulation of a surface with small genus is area rigid. For arbitrary surfaces we initiate a statistical study of the behavior of algebraic shifting, and in turn of area rigidity. We show that asymptotically almost surely the algebraic shifting of a random Delaunay triangulation of any given closed Riemannian surface is concentrated in a simplicial complex that depends only on the genus and the number of vertices. This talk is based on joint works with Eran Nevo and Yuval Peled.
] 11/11/2025
Jour férié (Armistice) 04/11/2025
Thomas Muller Higher dimensional floorplans and Baxter permutationsabstract.htmlA 2-dimensional mosaic floorplan is a partition of a rectangle by other rectangles with no empty rooms. These partitions (considered up to some deformations) are known to be in bijection with Baxter permutations. A d-permutation is a (d-1)-tuple of permutations.
In this talk, I will present a work in collaboration with Nicolas Bonichon and Adrian Tanasa where we introduce the d-floorplans which generalise the mosaic floorplans to arbitrary dimensions. I will first present the construction of their generating tree for which the corresponding labels and rewriting rules appear to be significantly more involved in higher dimensions. Then, I will present a bijection between the 2^{d-1}-floorplans and d-permutations characterised by forbidden vincular patterns, generalizing the bijection with Baxter permutations in the case d=2. Finally, I will present some work in progress on the "segments" of the 2^{d-1}-floorplans which relate d-floorplans to another class of d-permutations.
] 28/10/2025
Vacances (Toussaint) 21/10/2025
Fortuné Massamba Statistical geometry and the Goldberg conjectureabstract.htmlInformation geometry is an interdisciplinary field that uses the tools of differential geometry to explore and analyze probability theory and statistics. It focuses
on statistical manifolds, geometric spaces (Riemannian manifolds) whose points
represent different probability distributions. This geometric perspective provides
powerful insights into many fields among which information theory. In this talk, I
will present basic ideas about how to connect geometry and statistics, in particular
statistical manifolds and their Fisher metric. Finally, closer to my current research
themes, a statistical approach is discussed through the introduction of dual affine
connections associated with the metric on almost Kähler manifolds. This research
is motivated by the Goldberg conjecture, which asserts that a compact symplectic
manifold $(M, \omega)$ endowed with an $\omega$-compatible Einstein metric is Kähler.
] 14/10/2025
Réunion d'équipe 07/10/2025
Wenjie Fang Maximal number of subword occurrences in a wordabstract.htmlWe consider the number of occurrences of subwords (non-consecutive sub-sequences) in a given word. We first define the notion of subword entropy of a given word that measures the maximal number of occurrences among all possible subwords. We then give upper and lower bounds of minimal subword entropy for words of fixed length in a fixed alphabet, and also showing that minimal subword entropy per letter has a limit value. A better upper bound of minimal subword entropy for a binary alphabet is then given by looking at certain families of periodic words. We also give some conjectures based on experimental observations.
] 30/09/2025
Francis Durand Iterated grafting operators and preferential attachment graph modelsabstract.htmlIn this talk I will introduce the framework of
iterated grafting operators , an operator-based model for generating and analyzing combinatorial structures. This formalism naturally connects to partial differential equations and to the normal ordering problem in operator algebras, and provides powerful tools for enumeration. The combinatorial study of these objects was initiated by Blasiak and Flajolet in Philippe Flajolet’s last article
Combinatorial Models of Creation–Annihilation , but many aspects remain unexplored.
I will then focus on two specific models of preferential attachment graphs that arise from this approach. For these models, I will explain how to extract asymptotics from the associated generating functions using analytic techniques. Finally, I will discuss bijective correspondences with these graphs and open perspectives for random generation.
] 23/09/2025
Hadrien Notarantonio The 3-state Potts model on planar mapsabstract.htmlWe consider the 3-state Potts generating function $T(\nu, w)$ of planar triangulations; that is, the series in $\nu$ and $w$ counting planar triangulations with vertices coloured in $3$ colours, weighted by their size and by the number of monochromatic edges (variable $\nu$).
This series was proved to be algebraic $15$ years ago: this follows from its link with the solution of a discrete differential equation (DDE), and from general algebraicity results on such equations. However, despite recent progresses on the effective solution of DDEs, the exact value of had remained unknown so far. We have determined at last this exact value, proving that $T(\nu, w)$ satisfies a polynomial equation of degree $11$ in $T$. From this we determine the critical value of $\nu$ and the associated exponent.
Another approach, applied to the heavier case of general planar maps (still $3$-coloured) yields an equation of degree $22$.
Joint work with Mireille Bousquet-Mélou (LaBRI, Bordeaux)
] 16/09/2025
Élie de Panafieu Probability that voting strategically is pointlessabstract.html"Strategic voting" or manipulability by coalition, occurs when a group of voters can obtain an election outcome they prefer by not voting sincerely. Among the various existing voting systems, Instant-Runoff Voting (IRV) is reputed to be more resistant to strategic voting than others. IRV is used for several presidential and parliamentary elections around the world (Australia, India, Ireland, Papua New Guinea, Sri Lanka). We study the probability that strategic voting is ineffective under IRV when voters randomly draw their preferences among the candidates. This work combines social choice theory, probability, and analytic combinatorics.
] 09/09/2025
Mathieu Vallée Cônes, éventails, et biseaux: perspectives combinatoires et géométriques (soutenance de thèse AOC) 17/06/2025
Idrissa Kaboré Sur la complexité abélienne des mots infinisabstract.htmlLa complexité abélienne est un outil combinatoire qui calcule le nombre de vecteurs de Parikh de longueur donnée d'un mot infini. On appelle vecteur de Parikh d'un mot fini le vecteur formé par les nombres d'occurrences des lettres dans ce mot.
Cette complexité a connu une étude intensive depuis son introduction formelle par Richomme et al en 2009.
Dans cet exposé nous présenterons les fonctions de complexité de certains mots classiques (mots sturmiens, mots de Thue-Morse, mot de Tribonacci, ...) et quelques propriétés générales.
] 10/06/2025
Zoé Varin Analyse d'un algorithme probabiliste d'apprentissage par renforcement pour la recherche de plus courts chemins sur un grapheabstract.htmlOn étudie un processus d’apprentissage par renforcement, pour la recherche de plus courts chemins dans un graphe, dans lequel des fourmis partent d’un nid (aléatoire, N1 ou N2) et font une marche aléatoire (pondérée par les poids des arêtes) jusqu’à une source de nourriture F. À leur retour, elles renforcent les arêtes (en ajoutant 1 à leur poids) appartenant au chemin aller auquel on a enlevé les boucles inutiles. Ce modèle a déjà été étudié sur divers graphes dans le cas où le nid est déterministe, notamment les graphes séries-parallèles, mais aussi pour d’autres politiques de renforcements (articles de Kious, Mailler et Schapira). Nous étudions le cas à deux nids, dans des graphes obtenus en joignant trois graphes séries-parallèles pour former un triangle.
On montre que les poids des arêtes (normalisés) convergent, vers des variables aléatoires nulles si et seulement si les arêtes associées n’appartiennent pas à un plus court chemin d’un sommet de {N1 , N2 , F } à un autre.
Nous présenterons plusieurs outils utiles pour prouver cette convergence, notamment la comparaison avec des processus d'urnes, et quelques résultats sur les approximations stochastiques.
La présentation se basera sur un travail en commun avec Cécile Mailler.
] 03/06/2025
CAALM Complexity, Algorithms, Automata and Logic (2 au 6 juin) 20/05/2025
Juliette Schabanel Slit-Slide-Sew bijection for planar maps with prescribed degreesabstract.htmlDuring the last 20 years, integrable hierarchies (KP/Toda) have proven to be a great source of recurrence formulas for maps of all kinds. However, most of those formulas still lack a bijective explication. In this talk, we provide a bijective proof for the planar case of Louf's formula, which counts bipartite planar maps with prescribed face degrees and arises from the Toda hierarchy. We actually show that his formula hides two simpler formulas, both of which can be rewritten as natural equations on trees using duality and Schaeffer's bijection for eulerian maps. The underlying bijection for trees can also be interpreted directly on bipartite maps as " slit-slide-sew " operations. As far as we know, this is the first bijection for a formula arising from an integrable hierarchy with infinitely many parameters
] [vidéo ] 13/05/2025
Benjamin Testart Énumération des séquences d’inversions qui évitent des motifsabstract.htmlUne séquence d'inversions (ou table d'inversions) est une suite finie d'entiers (s_1, ..., s_n) telle que chaque terme s_i vérifie 0 ≤ s_i < i. Dans cet exposé, je présenterai différentes manières de construire ces séquences, qui permettent de les compter lorsqu'elles évitent des motifs. Je parlerai en particulier de constructions par "arbre de génération" et de quelques généralisations possibles de cette approche. Enfin, je donnerai un bref aperçu d'un travail en cours qui montre l'algébricité des fonctions génératrices des séquences d'inversions évitant certains ensembles de motifs.
] [vidéo ] 06/05/2025
Pallavi Panda Polytopal realisations of finite arc complexes using strip deformationsabstract.htmlA marked surface S is a finite-type possibly non-orientable surface with finitely many marked points (P) on the boundary and in the interior. These surfaces have long been studied both from a combinatorial as well as a geometric perspective. When the Euler characteristic of S\P is negative, the surface admits a finite-area hyperbolic metric. Such surfaces are called crowned surfaces, because their boundaries resemble a crown with spikes. Associated to marked/crowned surfaces is a combinatorial and topological object called the arc complex. This is a simplicial complex generated by arcs whose endpoints lie on the marked points. The arc complex has been used to understand the geometry of the surface by various mathematicians like Penner, Harer, Bowditch, Epstein. The arc complex is almost always infinite. In this talk we will focus on four families of surfaces for which it is finite. We will discuss how the topology of this complex helps us to understand certain deformations of crowned surfaces that weakly increase the "distances between spikes". As a result we get the non-simple polytopal realisations of these finite simplicial complexes. This is based ont the joint work with François Guéritaud. https://arxiv.org/abs/2505.01285
] [article ] [vidéo ] 29/04/2025
Worskhop au LAGA autour des homéomorphismes pseudo-Anosov 28-29-30 avrilabstract.htmlDans le cadre de notre projet ANR AnoDyn (Dynamique des flots d'Anosov), Vincent Delecroix, Pierre Dehornoy et moi organisons les 28, 29 et 30 avril, au LAGA, une rencontre groupe autour des
homéomorphismes pseudo-Anosov .
Un peu plus précisément, notre volonté est de présenter différentes approches combinatoires des homéomorphismes pseudo-Anosov (et certains de leurs « cousins ») permettant de résoudre de manière algorithmique, certaines questions concernant ces homéomorphismes : énumération, calcul de certains invariants, problème de conjugaison, etc. Nous prévoyons :
Un exposé de rappels . Classification de Nielsen-Thurston, qu'est-ce qu'un homéomorphisme pseudo-Anosov, un feuilletage singulier mesuré, une lamination géodésique, etc.
Une série de 3 exposés, par Christian Bonatti , sur la classification des difféomorphismes de Smale des surfaces à l'aide de type géométriques de partitions de Markov. Comment associer un difféomorphisme de Smale à un homéomorphisme pseudo-Anosov, notion de type géométrique d'une partition de Markov, caractérisation d'un difféomorphisme de Smale par un tel type géométrique, notion de genre d'un type géométrique, construction de type géométriques canoniques (types géométriques de première intersection).
Une série de 4 exposés, par Vincent Delecroix, Pierre Dehornoy et Jérôme Los , sur les différentes présentations combinatoires d'homéomorphismes pseudo-Anosov , les inductions associées, et leurs utilisations. Descriptions des pseudo-Anosov par échange d'intervalles, par réseaux ferroviaires (train-tracks), par action sur les triangulations et suites de « flips »,… Les graphes d'inductions associés. Comment cela permet de déterminer si un élément du mapping class group est de type pseudo-Anosov, d'énumérer les pseudo-Anosov, de résoudre le problème de conjugaison, etc.
Une série de 4 exposés, par Thomas de Mytteneare et François Béguin , sur l'utilisation de la géométrie du complexe des courbes pour analyser la dynamique des pseudo-Anosov (d'après Mark Bell, Richard Webb,...). Coordonnées d'une courbe par rapport à une triangulation, et manipulations algorithmiques de ces objets. Géométrie (hyperbolique) du graphe des courbes et construction en temps polynomial d'une approximation d'un domaine fondamental de l'axe d'un pseudo-Anosov. Calcul effectif de la longueur de translation d'une pseudo-Anosov, et d'un ensemble de triangulations canoniques.
Les exposés seront vraisemblablement relativement informels (le but étant d'apprendre et comprendre des mathématiques pour partie un peu anciennes) et l'ambiance celle d'un groupe de travail.
La rencontre aura lieu au LAGA à Villetaneuse . Elle débutera le 28 à 13h30 ou 14h, et se terminera le mercredi 30 à 16h environ. Il y aura a priori une douzaine d'exposés d'une heure (3 le lundi après-midi, 5 le mardi et 4 le mercredi). Pour des raisons d'organisation, si vous souhaitez participer à cette rencontre, je vous remercie de me le signaler (beguin@math.univ-paris13.fr ).
Programme
Lundi 13h30 - La classification de Nielsen-Thurston - Jérôme Los
Lundi 15h - Diifféomorphismes de Smale des surfaces et partitions de Markov (1) - Christian Bonatti
Lundi 16h30 - Construction via les échanges d’intervalles et l’induction de Rauzy - Pierre Dehornoy
Mardi 9h30 - Décrire et classer homéomorphismes les homéomorphismes pseudo-Anosov à l'aide de réseaux férroviaires - Jérôme Los
Mardi 11h - L'utilisation de la géométrie du graphe des courbes pour étudier les pseudo-Anosov (1) - François Béguin
Mardi 13h30 - Diifféomorphismes de Smale des surfaces et partitions de Markov (2) - Christian Bonatti
Mardi 15h - L'utilisation de la géométrie du graphe des courbes pour étudier les pseudo-Anosov (2) - Thomas de Mytteneare
Mardi 16h30 - Inductions : au-delà des échanges d’intervalles (1). Vincent Delecroix
Mercredi 11h - Inductions : au-delà des échanges d’intervalles (2). Vincent Delecroix
Mercredi 13h30 - Diifféomorphismes de Smale des surfaces et partitions de Markov (3) - Christian Bonatti
Mercredi 15h - L'utilisation de la géométrie du graphe des courbes pour étudier les pseudo-Anosov (4) - François Béguin
Résumés des exposés
La classification de Nielsen-Thruston. Jérôme Los (1 exposé)
Décrire et classer homéomorphismes les pseudo-Anosov à l'aide de réseaux férroviaires - Jérôme Los (1 exposé)
Construction et énumération d'homéomorphismes pseudo-Anosov via les échanges d’intervalles et l’induction de Rauzy. Pierre Dehornoy (1 exposé)
Inductions : au-delà des échanges d'intervalles. **Vincent Delecroix (2 exposés)
Difféomorphismes de Smale des surfaces et types géométriques de partitions de Markov. Christian Bonatti (3 exposés)
1 - Caractérisation de la dynamique d’un difféomorphisme de Smale par le type géométrique d’une partition de Markov
2 - Genre d’un type géométrique, types géométriques non-réalisables, types géométriques sans impasses. Liens entre difféomorphismes de Smale et homéomorphismes pseudo-Anosov.
3 - Points de première intersection, et partitions de Markov canoniques
L'utilisation de la géométrie du graphe des courbes pour étudier les pseudo-Anosov, d’après Masur-Minsky, Bell, Webb,… François Béguin et Thomas de Mytteneare (4 exposés)
1 - Les triangulations comme coordonnées pour les courbes et les homéotopies
2 - Arcs géodésiques dans le graphe des courbes
3 - Axe et longueur de translation d’un pseudo-Anosov dans le graphe des courbes
4 - Problème de conjugaison pour les pseudo-Anosov
] 08/04/2025
Howard Straubing Expressing properties of finite automata in variants of first-order logicabstract.htmlThis is a survey of research going back more than 60 years on the power of first order logic, along with various restrictions and extensions, to express the behavior of finite automata operating on strings over a finite alphabet. ‘Restrictions and extensions’ here means modifying the set of atomic formulas, bounding the quantifier depth, bounding the number of bound variables, etc. We want to be able to determine when a particular property (given in some other formalism, for example by a finite automaton) is expressible in the variant of first-order logic under study.
When the atomic formulas are restricted in such a way that only regular languages can be defined, there is an intricate mathematical apparatus, based in the algebraic theory of finite semigroups, that provides very precise answers to these questions. This will be the subject of the first part of the talk.
There are strong connections, known since the 1980’s, between this theory and questions about the complexity of fixed depth circuit families whose gates have unbounded fan-in. This, along with a few other extensions (for example, to automata operating on trees) and some recent results and open probems, will be explored in the second part of the talk.
] [vidéo ] 01/04/2025
Wissem Jedidi Extended internality with application to infinite divisible distributions [Slides.pdf ]abstract.htmlWe will discuss and extend results concerning a subclass of Bernstein functions,
the so-called internal Bernstein functions that where introduced by Bertoin, Roynette and Yor (Some connections between (sub)critical branching mechanisms and Bernstein functions, arXiv:math/0412322).
] [article ] [article ] [vidéo ] 01/04/2025
Roman Gambelin An extension of the algebraic Aldous diffusion [Slides.pdf ]abstract.htmlIn this talk, we introduce a sequence of Markov chains on trees with a fixed number leaves and study its scaling limit as the number of leaves tends to infinity. The chains are derived from Marchal's algorithm to approximate stable trees, and are a parameterized extension of a Markov chain on binary trees introduced by Aldous in 1998. When considered in a suitable space of trees, we will see that the chains converge to a diffusion which is symmetric with respect to the law of a stable tree. Our result relies on the theory of algebraic measure trees, developed by Winter and Löhr in 2018 and used by them in 2020 to prove the convergence of Aldous's chain, resolving an open problem posed by Aldous in 2000. After a presentation of the framework and statement, we will focus on the spectral decomposition of the limiting diffusion's generator and semigroup, providing a simple combinatorial description of their eigenspaces, and motivating their study by connecting it to several open questions regarding the process.
] [vidéo ] 01/04/2025
William Fleurat Croissance d'arbres BGW conditionnés de loi de reproduction log-concaveabstract.htmlJe parlerai de la construction de couplages croissants pour des modèles d'arbres aléatoires, dans le style de Luczak et Winkler ; c'est-à-dire dans lesquels les sommets sont ajoutés un par un, en s'assurant qu'à chaque étape l'arbre obtenu a la distribution voulue.
Je présenterai notamment le résultat suivant : étant donnée une loi de reproduction log-concave, la suite correspondante d'arbres de Bienaymé-Galton-Watson conditionnés à avoir $n$ sommets admet une réalisation sous la forme d'un processus markovien $(T_n, n\geq 1)$ qui ajoute une nouvelle feuille "sur la droite" à chaque étape.
Si le temps le permet, je discuterai d'une application à la construction de couplages croissants pour un modèle inhomogène de sous-arbres de l'arbre d'Ulam-Harris.
] [vidéo ] 01/04/2025
Thomas Simon Sur la loi limite de la marche de l'éléphant superdiffusiveabstract.htmlOn considère la marche aléatoire de l'éléphant sur $\mathbb Z$ dans le cas superdiffusif et on s'intéresse à la distribution limite renormalisée, qui est non-gaussienne. On donne le comportement asymptotique exact de la densité de cette distribution aux deux infinis, à l'aide d'une étude algébrique de la fonction génératrice des moments et d'un théorème taubérien fort. Dans le cas complètement asymétrique, on montre que la densité est unimodale et, dans certains cas, log-concave. Travail en collaboration avec Hélène Guérin (Montréal), Lucile Laulin (Nanterre) et Kilian Raschel (Angers).
] [vidéo ] 01/04/2025
Rafik Aguech Gaussian fluctuations of the elephant random walk with gradually increasing memory [Slides.pdf ]abstract.htmlThe elephant random walk (ERW) is a discrete-time random walk introduced by Schütz and Trimper (2004)
in order to investigate how long-range memory affects the behavior of the random walk. Its particularity is that the next step of the walker depends on its whole past through a parameter.
In this work, we investigate the validity of the central limit theorem of the ERW
when the walker has only a gradually increasing memory. Our contribution ) (joint work with Mohamed El Machkouri, University of Rouen)
provides a positive answer to a conjecture raised in a recent work by Gut and Stadtmüller
(2022 Stat. Probab. Lett.189 109598).
] [vidéo ] 01/04/2025
Journée MathSTIC "combinatoire et probabilités" (Rafik Aguech , William Fleurat , Roman Gambelin , Wissem Jedidi , Thomas Simon ) 25/03/2025
Zéphyr Salvy Unified study of block-weighted planar maps: combinatorial and probabilistic properties [Slides.pdf ]abstract.htmlThis talk focuses on classes of planar maps with a weight $u>0$ on certain components called \emph{blocks}. In collaboration with Fleurat, we study the decomposition of generic planar maps into $2$-connected components, revealing a phase transition between the universality classes of maps (converging to the Brownian sphere) and plane trees (converging to the Brownian tree), depending on the value of $u$. We identify a new class with the stable tree of parameter $3/2$ as the scaling limit in the critical case, and obtain precise results on block sizes in each phase. In a subsequent work, I show that it is possible to study many decomposition schemes along similar lines to shed light on a phase transition. I explain how to obtain enumerative results, block sizes and scaling limits for each phase. Finally, with Albenque and Fusy, we studied tree-rooted random planar maps decomposed into tree-rooted $2$-connected blocks, where a spanning tree is drawn simultaneously with the map. This model, which is of interest in theoretical physics, shows new behaviours. We determine the asymptotic behaviour of $2$-connected tree-rooted maps, reveal a phase transition, and study the properties of each phase.
] [vidéo ] [article ] 18/03/2025
Journées Aléa (17-21 mars)11/03/2025
Luca Castelli Aleardi Computation of toroidal Schnyder woods made simple and fast: from theory to practiceabstract.html
We consider the problem of computing Schnyder woods for graphs embedded on
the torus. We design simple linear-time algorithms based on canonical
orderings that compute toroidal Schnyder woods for simple toroidal
triangulations. The Schnyder woods computed by one of our algorithm are
crossing and satisfy an additional structural property: at least two of
the mono-chromatic components of the Schnyder wood are connected. We also
exhibit experimental results empirically confirming three conjectures
involving the structure of toroidal and higher genus Schnyder woods.
(to be presented at SoCG'25)
Joint work with Eric Fusy (Laboratoire d'Informatique Gaspard Monge),
Jyh-Chwen KO and Razvan Stefan Puscasu (LIX, Ecole Polytechnique)
] 04/03/2025
Rémi Maréchal Combinatoire énumérative et bijective de différentes familles de chemins de Dyck avec trous d'air [Slides.pdf ]abstract.htmlCet exposé se situe dans le cadre de la combinatoire des chemins sur réseau. On introduit ici une généralisation des chemins de Dyck (dits “avec trous d’air”), avant de se pencher sur diverses questions classiques à leur sujet : énumération, distributions de motifs, étude de sous-ensembles, etc. Ce faisant, des suites d’entiers positifs (connues dans la littérature) apparaissent naturellement. Dès que possible, on cherchera alors à relier les objets combinatoires décrits par ces suites aux chemins de Dyck avec trous d’air, à travers des bijections explicites.
Les travaux présentés ont été effectués pendant mon doctorat, et correspondent à trois publications dont les co-auteurs sont Jean-Luc Baril, Sergey Kirgizov, Helmut Prodinger, et Vincent Vajnovszki.
] [article ] [vidéo ] 25/02/2025
June Roupin
Alternating normal form in the standard braid monoid: local characterization, minimal automaton and automaticityabstract.htmlA braid can be seen as an equivalence class of words, and choosing a unique word representing each braid helps computing braids, motivating the study of normal forms. In the standard braid monoid, two such normal forms are the Garside normal form, which cuts a braid into a sequence of small simple braids, and the alternating normal form, which consists of recursively splitting a braid into a sequence of braids using less strands. The Garside normal form has many useful properties, in particular forming a regular and automatic language, as well as having a simple local characterization. On the other hand, only the regularity of the alternating normal was known. I will describe a new local characterization of the alternating normal form, explicitly construct its minimal automaton, and give some intuitions regarding its automaticity.
] 18/02/2025
Antoine Deza Kissing polytopesabstract.htmlA lattice (d,k)-polytope is the convex hull of a set of points in dimension d whose coordinates are integers ranging between 0 and k. We investigate the smallest possible distance between two disjoint lattice (d,k)-polytopes. This question arises in various contexts where the minimal distance between such polytopes appears in complexity bounds of optimization algorithms. We provide nearly matching lower and upper bounds for this distance and propose an algebraic model. Our formulation yields explicit formulas in dimensions 2 and 3, and allows for the computation of previously intractable values. Based on joint-work with Shmuel Onn (Technion), Sebastian Pokutta (Zuse Institute Berlin), and Lionel Pournin (Université Paris 13).
] 05/02/2025
ANR Flittla Journées "Complexité et la théorie de l'information" (Ivan Titov, Subin Pilari, Andrei Romashchenko)abstract.htmlTuesday, February 4th
] 04/02/2025
AG du LIPN à midi 04/02/2025
ANR Flittla Journées "Complexité et la théorie de l'information" (Geoffroy Caillat-Grenier, Alexander Shen, Thomas Seiller)abstract.htmlTuesday, February 4th
] 03/02/2025
Journées de combinatoire de Bordeaux (3-5 février)28/01/2025
Nabil Mustafa Online prediction in sub-linear spaceabstract.htmlIn this talk, I will present the main ideas from this paper:
Online Prediction in Sub-linear Space, B. Peng and F. Zhang, SODA 2023 (best student paper award).
It gives new low-space algorithms for the regret minimisation problem in learning theory.
Precious little is required in the way of prerequisites, except that you be intelligent enough to be interested in this sort of thing.
The talk will start from the basics (the experts problems), and then cover the new ideas to entend classical learning algorithms to work, approximately, with sub-linear space.
] [article ] 21/01/2025
Hsien-Kuei Hwang Laplace's and Cauchy's contributions to the Stirling partition numbersabstract.htmlPierre-Simon Laplace (1749-1827) is widely recognized for his monumental works, Théorie analytique des probabilités and Mécanique céleste. Augustin-Louis Cauchy (1789-1857), on the other hand, revolutionized classical operational analysis by formalizing it with a rigorous foundation, laying the groundwork for modern calculus and complex analysis. However, their contributions to the Stirling partition numbers remain largely overlooked in the combinatorial literature, a gap this talk aims to address.
By examining their lesser-known work on Stirling partition numbers through a historical lens and integrating modern methodological perspectives, the presentation highlights the intersection of their insights with the combinatorial framework of Stirling numbers, offering new appreciation for their contributions to this area of mathematics. This research is based on ongoing joint work with Chong-Yi Li and Vytas Zacharovas.
] 07/01/2025
Nicolas Grenèche Présentation de la plate-forme de calcul (MAGI) de l'université 17/12/2024
collectif
Groupe de lecture surfaces de translation 10/12/2024
Imre Bárány A matrix version of the Steinitz lemmaabstract.htmlSteinitz's lemma is about a finite set $V$ of at most unit vectors in $R^d$ whose sum equals zero. It states that the elements of $V$ can be ordered so that all partial sums along this ordering have norm at most 2d. I'm going to explain and prove a matrix version of this lemma. Moreover, I plan to give a bouquet of open questions from various areas of discrete and convex geometry.
] [article ] 10/12/2024
Niloufar Fuladi Cross-cap drawings and signed reversal distance [Slides.pdf ]abstract.htmlA cross-cap drawing of a graph G is a drawing on the sphere with g distinct points, called cross-caps, such that the drawing is an embedding except at the cross-caps, where edges cross properly. I will first outline a connection between cross-cap drawings and an algorithm coming from computational biology to compute the signed reversal distance between two permutations. Then I will explain how this connection can be leveraged to answer two computational problems on graphs embedded on surfaces.
This is joint work with Alfredo Hubard and Arnaud de Mesmay.
] [vidéo ] 03/12/2024
Ulysse Léchine Complexity theory (soutenance de thèse équipe LOVE) 03/12/2024
Grégory Miermont Aspects combinatoires, probabilistes et géométriques des cartes (colloquium du LAGA) 26/11/2024
János Pach Slabs, slobs, and other distractionsabstract.htmlSome of my favorite problems that require no prerequisites. For instance, given an infinite collection of slabs in 3-space with divergent total width, can we translate each of them so that altogether they cover the unit ball?
] 26/11/2024
Réunion d'équipe 19/11/2024
Réunion d'équipe 19/11/2024
Philippe Marchal Talagrand's concentration inequality (groupe de travail "Complexités ") [Slides.pdf ] [vidéo ] 12/11/2024
Pascal Weil Étude combinatoire et asymptotique des sous-groupes du groupe libreabstract.htmlÀ chaque sous-groupe H du groupe libre, on peut associer un unique graphe, dit graphe de Stallings de H, qui a des propriétés remarquables : il est fini si H est finiment engendré, calculable en temps presque linéaire à partir d'un ensemble de générateurs de H, et il permet de résoudre élégamment et efficacement un grand nombre de problèmes algorithmiques : calcul du rang et d'une base de H, calcul de l'index de H, calcul de l'intersection de deux sous-groupes, résolution du problème de l'appartenance uniforme… Des choses plus exotiques aussi, comme le calcul de la clôture pro-p de H ou de sa clôture algébrique.
Comme ce graphe fini est assez contraint, on peut utiliser la combinatoire pour énumérer les graphes de Stallings et donc les sous-groupes, les générer aléatoirement, et aborder des questions asymptotiques : quelle est l'espérance du rang d'un sous-groupe du groupe libre, quelle est la probabilité qu'il soit d'indice fini, etc… On peut aussi évaluer la complexité en moyenne du problème de l'appartenance uniforme.
La notion de graphe de Stallings peut être étendue aux sous-groupes quasi-convexes des groupes hyperboliques, et à des classes un peu plus larges. On y conserve la calculabilité. On peut par exemple étendre au groupe modulaire certains résultats algorithmiques et asymptotiques sur le groupe libre.
Ma présentation sera appuyée sur la littérature classique (à commencer par Stallings 1983) et sur mes travaux, menés pour l'essentiel avec Frédérique Bassino et Cyril Nicaud.
] 08/11/2024
Journées MathStic CombiGéométrie Hugo Parlier / Guilherme Dias da Fonseca / Ludovic Morin / Alexandre Louvet 07/11/2024
Journées MathStic CombiGéométrie Janos Pach / Wolfgang Mulzer / Sophie Huiberts 05/11/2024
Florent Koechlin Une borne sur le nombre de triangulations de \(n\) points dans le planabstract.htmlEn mode groupe de travail, nous verrons via quelle méthode Sharir et Welzl (en 2009) ont obtenu une borne sup pour le nombres de triangulations de $n$ points.
Voir aussi la discussion https://cstheory.stackexchange.com/questions/8565/the-number-of-triangulations-of-a-set-of-n-planar-points-why-so-difficult
] [article ] 15/10/2024
Morgan Rogers From free idempotent monoids to free multiplicatively idempotent rigs [article ] 15/10/2024
AG du LIPN (9h30-12h30) 10/10/2024
Séminaire Flajolet Marthe Bonamy, Nicolas Broutin, Florent Hivert 08/10/2024
Réunion d'équipe (poste MdC, potentiels nouveaux arrivants...) 04/10/2024
Journées MathStic Combinatoire et Probabilités Michael Drmota/Alice Contat/Andrew Elvey-Price/Enrica Duchi/Quentin Berger 03/10/2024
Journées MathStic Combinatoire et Probabilités Mireille Bousquet-Mélou/ Mingkun Liu /Armand Riera/Meltem Ünel /Baptiste Louf 01/10/2024
Gabriele Sicuro Machine learning and heavy-tailed covariates in high dimensions [Slides.pdf ]abstract.htmlMachine learning theoretical models very often assume a dataset obtained from a Gaussian distribution, or from a Gaussian mixture. The possible limitations of such a Gaussian assumption have been recently object of investigation, and theoretically characterization,
leading to a number of "Gaussian universality" results. In this talk I will present an analytical treatment of the performance in high dimensions of simple architectures on heavy-tailed distributed datasets, showing that even simple generalized linear models exhibit
a striking dependence on non-Gaussian features in both classification and regression tasks.
] [article ] [article ] 24/09/2024
Journée MathStic
Mathématiques, apprentissage et réseauxabstract.htmlOrganisatrices : Thi Mai Trang Nguyen (L2TI), Thanh Mai Pham Ngoc (LAGA) et Céline Rouveirol (LIPN)
Programme :
] 17/09/2024
Réunion d'équipe 11/09/2024
Michael Drmota The magic number pi: computation and proof of irrationality (talk for the students, EUR Math&CS) 10/09/2024
Javier Fresán Quelques progrès récents sur les fonctions G et les fonctions Eabstract.htmlLes fonctions G et les fonctions E sont des séries entières à coefficients algébriques qui sont solution d'une équation différentielle
et satisfont à des conditions de croissance de nature arithmétique. Elles correspondent aux fonctions holonomes/D-finies qui apparaissent dans de nombreux problèmes
en combinatoire, probabilité, physique.
Elles ont été introduites dans le mémoire de Siegel sur les
applications de l'approximation diophantienne en 1929, dans le but de généraliser les résultats de transcendence pour les valeurs de la fonction exponentielle en des arguments algébriques. Je survolerai de façon accessible quelques progrès récents, voire très
récents, et moins récents sur les fonctions G et les fonctions E, en mettant l'accent sur deux questions : quelle est la structure de leurs équations différentielles ? quelle place occupent les fonctions hypergéométriques parmi elles ?
] [article ] 05/07/2024
Journées ANR 3DMAPS
Eleanor Archer , Luca Lionni , Alicia Castro [abstract.pdf ]04/07/2024
Journées ANR 3DMAPS
Éric Fusy , Ariane Carrance , Valentin Bonzon , Johannes Thüringen , Carole Porrier , Arnauld Solente [abstract.pdf ]03/07/2024
Journées ANR 3DMAPS
Victor Nador , Thomas Müller , Luca Castelli Aleardi [abstract.pdf ]01/07/2024
AG du LIPN 25/06/2024
Philippe Di Francesco'60th birthday: Integrable combinatorics : Lauren Williams, Andrea Sportiello, Filippo Colomo, Philippe Biane24/06/2024
Gascom 2024 (24-28 juin)18/06/2024
Daniel Krenn Multi-pivot quicksort and how to compute precise asymptotics (retransmission depuis la conf AofA) 18/06/2024
AofA 2024 (17-21 juin)11/06/2024
vote responsable & représentant d'équipe 06/06/2024
Séminaire Flajolet Gilles Schaeffer/Aline Parreau/Baptiste Rognerud 04/06/2024
Oriane Blondel A random Markov property for random walks in dynamic random environments (séminaire de proba du LAGA ) 28/05/2024
Bishal Deb Lattice paths and branched continued fractions: Coefficientwise Hankel total positivity of the Laguerre polynomials [Slides.pdf ]abstract.htmlThe Laguerre polynomials are a family of orthogonal polynomials which
have been well-studied in combinatorics.
The coefficients of these polynomials enumerate a certain family of
graphs which have been called Laguerre digraphs or Laguerre
configurations.
The polynomial sequence has a well-known Stieltjes moment
representation, i.e., these polynomials can be expressed as the
sequence of moments of a certain measure supported on the positive
real-axis.
It is known that a sequence is a Stieltjes moment sequence if and only
if its Hankel matrix is totally positive.
A natural question is to ask if the Hankel matrix is also
coefficientwise totally positive.
We will address this question in this talk.
We will begin by stating the main theorem which will not require any
prerequisites.
We then motivate this result;
we first state the equivalence between Stieltjes moment sequences
and the total positivity of Hankel matrices,
then we mention how this theory has been extended coefficientwise.
We introduce the production-matrix method which is a powerful tool to
prove total positivity.
Finally, we sketch a proof of our main theorem.
] [article ] [vidéo ] 21/05/2024
Kavitha Telikepalli Popular assignments and extensions [Slides.pdf ]abstract.htmlThis talk will be on popular matchings in the one-sided preferences model. Popular matchings need not always exist in this model and there is a simple combinatorial algorithm to decide if one exists. We will see an LP-duality inspired algorithm for the more general
problem of deciding if a popular assignment (i.e., a popular maximum-matching) exists or not. This algorithm can be generalized to solve the popular common base problem in the intersection of two matroids where one matroid is the partition matroid, this implies the
popular arborescence problem (relevant in liquid democracy) can be solved efficiently.
] [vidéo ] [vidéo ] 14/05/2024
Kavitha Telikepalli Popular matchings and optimality [Slides.pdf ]abstract.htmlIn this talk we will consider algorithms for finding optimal popular matchings. While it is easy to find max-size popular matchings, it is NP-hard to find a min-cost popular matching. This motivates us to relax popularity to a weaker notion called
"quasi-popularity". Describing the popular and quasi-popular matching polytopes is hard, but there is an easy-to-describe integral polytope sandwiched between these two hard ones (see the illustration). So we can efficiently find a quasi-popular matching of cost at
most that of a min-cost popular matching.
] [vidéo ] 07/05/2024
Kavitha Telikepalli Introduction to popular matchings [Slides.pdf ]abstract.htmlThe problem of computing a stable matching in a bipartite graph is an old and well-studied problem. Gale and Shapley showed in 1962 that such a matching always exists and can be efficiently computed. This is a classical result in algorithms with many applications in
economics and computer science. Stability is a strong and rather restrictive notion. This series of talks will be on a relaxation of stability called "popularity". In the first talk we will see simple and efficient algorithms for some popular matching problems. No
background in algorithms or matching theory will be assumed.
] [vidéo ] 07/05/2024
Pallavi Panda Topology of the arc complex [Slides.pdf ]abstract.html The arc complex is a pure flag simplicial complex associated to a finite-type topological surface with marked points. It was discovered by Harvey and used by geometers like Harer, Penner, Bowditch, Epstein to study geometric properties of hyperbolic surfaces,
their Teichmüller spaces and their mapping class groups. The arc complex is also a subcomplex of the cluster complex of a cluster algebra, defined by Fomin-Zelevinksy. For most of the surfaces, the arc complex is locally non-compact. In this talk, I will discuss
about the simplicial topology of the arc complex in the finite cases. In particular, I will focus on the shellability (analogous to simply-connectedness) and collapsibility (analogous to contractibility) of these finite complexes and prove that they are closed
combinatorial balls.
] [article ] [article ] [vidéo ] 30/04/2024
Matteo D'Achille Les bijoux de la tessellation idéale de Poisson-Voronoï de l'espace hyperboliqueabstract.htmlNous discuterons de la limite de faible intensité des tessellations de Poisson--Voronoï sur les espaces hyperboliques, alias tessellations idéales de Poisson--Voronoï (IPVT de l'anglais). En particulier, nous verrons comment une simple description poissonnienne de la cellule qui contient l'origine de l'espace hyperbolique (cellule zéro) permet d'étudier des propriétés fines des tuiles de l'IPVT. L'exposé présentera des impressions en 3D de réalisations de la cellule zéro de l'IPVT de l'espace hyperbolique tridimensionnel dans le modèle de la boule de Poincaré.
Travail en collaboration avec Nicolas Curien, Nathanaël Enriquez, Russell Lyons et Meltem Ünel.
Pour en savoir plus sur les bijoux : https://matteodachille.github.io/ipvt">https://matteodachille.github.io/ipvt
] [article ] [vidéo ] 23/04/2024
Michael Wallner Combinatorics of non-deterministic walksabstract.htmlWe introduce nondeterministic walks, a new variant of one-dimensional discrete walks.
The main difference to classical walks is that its nondeterministic steps consist of sets of steps from a predefined set such that all possible extensions are explored in parallel.
We discuss in detail the nondeterministic Dyck step set $\{ \{-1\}, \{1\}, \{-1,1\}\}$ and Motzkin step set $\{\{-1\}, \{0\}, \{1\}, \{-1,0\}, \{-1,1\}, \{0,1\}, \{-1,0,1\}\}$,
and show that several nondeterministic classes of lattice paths, such as nondeterministic bridges, excursions, and meanders are algebraic.
The key concept is the generalization of the ending point of a walk to its reachable points, i.e., a set of ending points.
We extend our results to general step sets:
We show that nondeterministic bridges and several subclasses of nondeterministic meanders are always algebraic.
We conjecture the same is true for nondeterministic excursions, and we present python and Maple packages to support our conjecture.
This research is motivated by the study of networks involving encapsulation and decapsulation of protocols.
Our results are obtained using generating functions, analytic combinatorics, and additive combinatorics.
Joint work with Élie de Panafieu.
] [article ] [vidéo ] 16/04/2024
Patrick Teller Comment réduire à la main une matrice non-négativeabstract.htmlPuisque la réductibilité d'une matrice M se traduit à la fois en termes de conjugaison avec une matrice contenant un bloc nul et en termes de positivité de ses puissances,
il a paru intéressant d'étudier la présence et la persistance de termes nuls (les zéros) dans les différentes puissances de M.
] 02/04/2024
Eleanor Archer Limite d'échelle des arbres couvrants aléatoires [Slides.pdf ]abstract.htmlUn arbre couvrant d'un graphe connexe fini G est un sous-graphe connexe de G qui contient chaque sommet et ne contient aucun cycle.
Un résultat bien connu d'Aldous énonce que la limite d'échelle de l'arbre couvrant uniforme du graphe complet est l'arbre brownien. En fait cet énoncé est plus général :
l'arbre brownien est la limite d'échelle des arbres couvrants uniformes pour un grand ensemble de graphes en grande dimension. Dans cet exposé, nous allons essayer d'expliquer ce phénomène universel,
à l'aide des algorithmes d'échantillonnage. Si le temps nous permet, nous allons également discuter des limites d’échelle des arbres couvrants aléatoires non-uniformes. Travaux en collaboration avec Asaf Nachmias et Matan Shalev.
] [article ] [vidéo ] 26/03/2024
Thomas Fernique Enforcing 3x3 substitutions by matching rules [Slides.pdf ]abstract.htmlA combinatorial substitution is a map over tilings which allows to
define sets of tilings with a strong hierarchical structure.
We show that such sets of tilings are sofic, that is, can be enforced by finitely many local
constraints. This extends some similar previous results (Mozes’90, GoodmanStrauss’98) in a shorter presentation.
] [article ] [vidéo ] 19/03/2024
Meltem Ünel Limite locale des arbres pondérés exponentiellement par la hauteurabstract.htmlLe cas le plus simple et peut-être le plus naturel des limites locales des arbres est Uniform Infinite Planar Tree: on commence par la suite des mesures de probabilité uniforme $\nu_N$ dont le support est l’ensemble des arbres planes enracinés de taille $N$ et on étudie
la limite faible $\nu$ de cette suite, dont le support est l'ensemble des arbres plans enracinés de taille infinie.
Une modification naturelle dans la recherche des limites différentes est de pondérer les arbres:
est-ce que la nouvelle suite des mesures $\rho_N$, par rapport à laquelle la valeur d’un arbre de taille N est proportionnelle à son poids, admet une limite faible?
Dans cet exposé, on considère des arbres plans enracinés dont la distribution est uniforme pour une hauteur $h$ et une taille $N$
fixées et dont la dépendance à la hauteur est de forme exponentielle, $\exp(-\mu h)$, pour $\mu$ réel.
En définissant le poids total de ces arbres de taille $N$ fixe comme $Z^{\mu} _N$, on détermine son comportement asymptotique pour $N$ grand, pour $\mu$ réel quelconque. Finalement, on identifie la limite locale des mesures de probabilité correspondantes et on trouve une transition à $\mu=0$ d'une phase à une
seule épine à une phase à plusieurs épines (backbone).
En conséquence, il y a une transition dans le taux de croissance du volume des boules autour de la racine en fonction du rayon, passant d'une croissance linéaire pour $\mu < 0$
à la croissance quadratique familière pour $\mu=0$ et à une croissance cubique pour $\mu > 0$.
] [article ] [vidéo ] 12/03/2024
Journées Aléa (11-15 mars, CIRM) 05/03/2024
Slim Kammoun Asymptotic normality of pattern counts in conjugacy classes [Slides.pdf ]abstract.htmlIn a joint work with Valentin Féray, we prove, under mild conditions on fixed points and two cycles, the asymptotic normality of vincular pattern counts for a permutation chosen uniformly at random in a conjugacy class.Additionally, we prove that the limiting variance is always non-degenerate for classical pattern counts. The proof uses weighted dependency graphs.
] [article ] [vidéo ] 27/02/2024
Patrick Schnider Combinatorial depth measures [Slides.pdf ]abstract.htmlCombinatorial depth measures are a way to generalize the concept of medians to higher dimensions, formalizing our intuition that some query points lie „deeper“ within a set of data points than others. Several such measures have been introduced in the last century,
such as Tukey depth or Simplicial depth. Many fundamental problems in discrete geometry, such as the centerpoint theorem or Tverberg’s theorem, can be phrased naturally in terms of depth measures. In my talk, I consider families of combinatorial depth measures
defined by natural sets of axioms and show that they cannot differ too much.
] [article ] [vidéo ] 20/02/2024
vacances de février 13/02/2024
Alice Contat Parking sur l'arbre binaire infini [Slides.pdf ]abstract.html Considérons un arbre enraciné dont les sommets seront interprétés comme des places de parking, chaque place pouvant accueillir au maximum une voiture. Sur chaque sommet de l’arbre, on ajoute une étiquette entière et positive représentant le nombre de voitures
arrivant sur ce sommet. Chaque voiture essaie de se garer sur son sommet d'arrivée et, si la place est occupée, elle descend en direction de la racine de l'arbre jusqu'à ce qu'elle trouve un sommet vide où se garer. S'il n'y a pas de sommet libre sur le chemin vers
la racine, la voiture sort de l'arbre, contribuant ainsi au flux de voitures à la racine. Ce modèle présent une transition de phase intéressante que nous allons analyser en détail. Après un aperçu du cas où l'arbre sous-jacent est un arbre critique de
Bienaymé-Galton-Watson, nous nous concentrerons sur le cas de l'arbre binaire infini, où la transition de phase qui s'avère être "discontinue". Si le temps le permet, je montrerai que notre technique s’applique également aux arbres surcritiques avec loi
géométrique, grâce aux résultats d’énumération de Linxiao Chen.
L'exposé est basé sur un travail joint avec David Aldous, Nicolas Curien et Olivier Hénard, et avec Linxiao Chen.
] [article ] [vidéo ] 06/02/2024
Journées de combinatoire de Bordeaux (5-7 février) 30/01/2024
Mehdi Naima A lattice on Dyck paths close to the Tamari lattice [Slides.pdf ]abstract.htmlWe introduce a new poset structure on Dyck paths where the covering relation is a particular case of the relation inducing the Tamari lattice. We prove that the transitive closure of this relation endows Dyck paths with a lattice structure. We provide a trivariate generating function counting the number of Dyck paths with respect to the semilength, the numbers of outgoing and incoming edges in the Hasse diagram. We deduce the numbers of coverings, meet and join irreducible elements. We give a generating function for the number of intervals, and we compare this number with the number of intervals in the Tamari lattice. Finally, we present a sequent calculus capturing this new Lattice.
] [article ] [vidéo ] 23/01/2024
Victor Nador Polynômes de Jack et constellations b-déformées [Slides.pdf ]abstract.htmlLa série génératrice des cartes orientables pondérées (et sa
généralisation aux constellations) peut s’exprimer simplement à l’aide
des fonctions de Schur. La série des cartes non-orientées (c’est-à-dire orientable ou non) admet une expression similaire où les
fonctions de Schur sont remplacées par les polynomes zonaux. Dans ces
deux cas, il existe une grande diversité d’outil permettant d’étudier
ces objets: théorie des représentations, décomposition combinatoires,
lien avec la théorie des matrices aléatoires, propriétés
d’intégrabilité, etc. Les polynômes de Jack sont une déformation à un
paramètre $b$ (dite b-déformation) qui interpole ces deux cas.
Seulement, la déformation rend plus délicate l’étude de la série
génératrice associé, source de deux conjectures proposées par Goulden
et Jackson en 96.
Dans cet exposé, je rappellerai les propriétés des constellations
b-déformées introduites récemment par Chapuy et Dolega et soulignerait
certaines des difficultés induite par la b-déformation pour étudier
ces objets. Je présenterai des résultats récents en collaboration avec
V. Bonzom nous permettant d’extraire un ensemble d’EDP pour certains
modèle de constellations. Je parlerai également de travaux en cours
permettant de donner une interprétation géométrique du poids en b des
constellations.
] [article ] [vidéo ] 16/01/2024
Florent Koechlin A canonical tree decomposition for chirotopes [Slides.pdf ]abstract.htmlDans cet exposé, je présenterai une notion d’arbre de décomposition d’un ensemble de points dans le plan (plus précisément de son chirotope, la fonction qui encode l'orientation de tout triplet de point de l'ensemble). Cette décomposition, qui s'appuie sur le
concept d'ensembles de points s'évitant mutuellement ("mutually avoiding sets"), s'inspire de la décomposition modulaire des graphes. J'expliquerai pourquoi cette décomposition est canonique, et comment elle peut être utilisée pour calculer le nombre de
triangulations d'un chirotope à l'aide de sa décomposition. Il s'agit d'un travail commun avec Mathilde Bouvel, Valentin Féray et Xavier Goaoc.
In this talk, I'll introduce a notion of decomposition tree of a planar point set (more precisely, of its chirotope, that is the function encoding the orientation of any triplet of points in the set). This decomposition relies on the concept of mutually avoiding
point sets, and is inspired by the modular decomposition of graphs. I'll explain why this decomposition is canonical, and how it can be used to compute the number of triangulations of a chirotope using its decomposition. This is a joint project with Mathilde Bouvel,
Valentin Féray and Xavier Goaoc.
] [vidéo ] 19/12/2023
Benjamin Dequêne Une nouvelle famille de bijections entre les partitions non-croisées et les partitions non-imbriquées [Slides.pdf ]abstract.htmlAssocié à un groupe de Weyl, il y a deux ensembles d’objets combinatoires, comptés par les nombres de Catalan généralisés,
qui s’appellent les partitions non-croisées et les partitions non-imbriquées.
Ces objets ont des liens très intéressants avec la théorie des
représentations d’algèbres : pour ne citer qu’un résultat, par exemple, les partitions non-croisées sont en bijection avec les sous-catégories "wide"
de la catégorie des modules sur des algèbres héréditaires de type finie. La question d’une relation exacte entre ces
deux objets n’admet que des réponses partielles. Récemment, nous avons mis en lumière des liens supplémentaires, renforçant certains liens déjà connus, dans le cas du groupe symétrique :
pour tout élément de Coxeter standard, nous construisons une bijection
équivariante entre les partitions non-croisées sous l’action du complément de Kreweras et les partitions non imbriquées sous une action cyclique particulière, que nous appelons le complément de Kroweras. Cette bijection équivariante, construites à partir de règles
locales, est l’unique bijection qui est à la fois équivariante et qui préserve le support. Dans cet exposé, je vais tenter de faire le tour de tous les ingrédients nécessaires, en exposant des aspects davantage tirés vers la théorie des représentations, afin
d’aboutir à la construction de cette bijection. Ces travaux sont en collaboration avec Gabriel Frieden, Alessandro Iraci, Florian Schreier-Aigner, Hugh Thomas et Nathan Williams.
] [vidéo ] 12/12/2023
Journées Hcéres du LIPN (12-14 décembre) 05/12/2023
Workshop: Computer Algebra for Functional Equations in Combinatorics and Physics (IHP, 4-8 décembre)28/11/2023
Recent Trends in Computer Algebra 2023 (IHP, 27 novembre-1 décembre)27/11/2023
Théophile Buffière Théorèmes combinatoires et probabilistes sur certaines familles de polytopes (soutenance de thèse)abstract.html La richesse de l'étude combinatoire des polytopes repose grandement sur le paradoxe entre leur extrême banalité dans toutes sphères des mathématiques et la grande difficulté à établir des théorème combinatoires généraux sur ceux-ci. En prenant une sous-famille des
polytopes, les zonotopes, dont la structure est beaucoup plus algébrique, nous avons démontré un certain nombre de résultats énumératifs asymptotiques. Tout d'abord sur le nombre de types combinatoires de polytopes équiprojectifs, ce qui ouvre de nouvelles
perspectives sur une question ouverte posée par Shephard en 1968 d'une construction explicite de tous ces polytopes. Ensuite, dans le domaine des polytopes entiers, c'est à dire les polytopes dont les sommets sont de coordonnées entières (dans R^d), nous avons
calculé l'équivalent asymptotique du nombre de zonotopes entiers dans un hypercube. Ce résultat nous permet d'améliorer les résultats de Barany Bureau et Lund en donnant le deuxième ordre de la convergence d'un zonotope entier dans un cône dont les deux extrémités
sont fixées.
Tout cela nous permet enfin d'établir un théorème limite fonctionnel pour les polygones entiers uniformément aléatoires dans un carré, où apparaît un pont Brownien avec une dérive étonnante, car c'est une courbe cubique.
] 23/11/2023
Vu Dinh Towards Picard-Vessiot theory for noncommutative differential equations (soutenance de thèse) 21/11/2023
Ali Khezeli An improved lower bound on the largest common subtree of random leaf-labeled binary trees (exposé online au Applied Mathematics Webinar ) 21/11/2023
Journée des doctorants 15/11/2023
Combinatorics and Arithmetic for Physics (15-17 Nov., IHÉS)14/11/2023
Nabil Mustafa The Clarkson-Shor technique: a powerful probabilistic technique for combinatorial bounds 07/11/2023
Jean Cardinal Mini-cours "Flip graphs and matroids" (16h-19h) [Slides.pdf ] 03/11/2023
Carole Porrier Constructions quasipériodiques : ensembles de tuiles apériodiques et sous-arbres induits optimaux dans des pavages substitutifs (soutenance de thèse)abstract.htmlUn pavage du plan est composé d'ensembles fermés appelés tuiles, qui couvrent le plan euclidien sans trou ni chevauchement. Ma thèse porte sur des pavages quasipériodiques : bien qu'ils ne soient pas périodiques, on y trouve partout les mêmes motifs finis et leurs
propriétés peuvent être assez fortes. Les plus connus sont les pavages de Penrose, qui combinent un grand nombre de propriétés. On peut en effet les définir par des règles locales, des substitutions, par coupe et projection, ou comme système dynamique symbolique. De
manière générale, les pavages quasipériodiques se définissent par une seule de ces méthodes, et on se demande quels liens il peut y avoir entre différentes façons de les définir ou représenter.
La structure combinatoire d'un pavage peut être étudiée via le graphe d'adjacence des tuiles (ou graphe dual). Dans un tel graphe, on s'intéresse aux sous-arbres induits ayant le plus grand nombre possible de feuilles à nombre n de sommets fixé. La suite de ces
maxima est appelée ``fonction feuille''. Dans ma thèse, je détermine la formule de la fonction feuille des pavages de Penrose, en utilisant les substitutions et règles locales pour exhiber une famille de sous-arbres induits ``pleinement feuillus'' arbitrairement
grands.
Ensuite, comme les barres d'Ammann des pavages de Penrose joué un rôle dans l'étude du problème ci-dessus, on tente de mieux les comprendre via la notion de sous-périodes, qui découlent d'un schéma de coupe et projection. On définit grâce à celles-ci une méthode
permettant de trouver des barres d'Ammann pour de nombreux pavages, en construisant des jeux de tuiles décorées, qui sont apériodiques. Les pavages en questions peuvent alors être obtenus en assemblant les tuiles façon puzzle plutôt que par coupe et projection.
Enfin, en utilisant les règles locales, on construit aussi un jeu de tuiles de Wang associé aux pavages golden octagonal. La démarche suivie permet en outre d'établir un lien explicite entre schéma de coupe et projection et partition de Markov offrant une
représentation symbolique de ces pavages. Le caractère substitutif des pavages golden octagonal est montré.
Jury :
] 26/10/2023
Daria Pchelina Densité des arrangements de disques et des empilements de sphères (soutenance de thèse)abstract.htmlComment empiler un nombre infini d’oranges pour maximiser la proportion de l’espace couvert ? Kepler a conjecturé que l’empilement des "balles de canon" est optimal. 400 ans se sont écoulés avant que cette conjecture soit démontrée par Hales et Ferguson dont la
preuve comporte 6 papiers et des dizaines de milliers de lignes de code informatique.
Comment arranger un nombre infini de pièces de monnaie de 3 rayons différents sur une table infinie pour maximiser la proportion de la surface couverte ? Un arrangement de disques est dit triangulé si chacun de ses "trous" est borné par trois disques mutuellement
tangents. Connelly a conjecturé que si de tels arrangements existent, l’un d’eux maximise la proportion de la surface couverte; cela est vrai pour les arrangement unaires et binaires.
Dans cette thèse, nous étudions diverses techniques utilisées dans la preuve de la conjecture de Kepler ainsi que dans d’autres résultats importants de le domaine des arrangements de disques et de sphères, tels que la redistribution de la densité locale basée sur la
recherche par l’ordinateur et l’arithmétique d’intervalles. Cela nous permet de prouver l’assertion de la conjecture de Connelly pour 31 triplets de rayons de disques triangulés et de la réfuter pour 45 autres triplets. En outre, nous obtenons des bornes précises
sur la densité locale des cellules simpliciales dans les empilements à 2 sphères en 3D.
Jury :
Sandor Fekete, Univ. de Braunschweig - Rapporteur
Thomas Fernique, USPN - Directeur
Xavier Goaoc, Univ. de Lorraine - Examinateur
Nabil Mustafa, USPN - Examinateur
Michael Rao, ENS de Lyon - Rapporteur
Nathalie Revol, ENS de Lyon - Examinatrice
Guillaume Theyssier, Univ. d'Aix-Marseille - Examinateur
La présentation sera en anglais et sera suivie d'un pot en salle café (A201) auquel vous êtes également invités.
Pour plus de détails, https://lipn.univ-paris13.fr/~pchelina/PhD_defense.html
] 24/10/2023
Jean Cardinal Mini-cours "Flip graphs and matroids" (17h-18h45) [Slides.pdf ] 17/10/2023
Li Gan Signed area of lattice paths and exclusion statistics [Slides.pdf ]abstract.htmlWe study the enumeration of closed walks of given length and algebraic area on the honeycomb lattice. Using an irreducible operator realization of honeycomb lattice moves, we map the problem to a Hofstadter-like Hamiltonian and show that the generating function of
closed walks maps to the grand partition function of a system of particles with exclusion statistics of order g=2 and an appropriate spectrum, along the lines of a connection previously established by two of the authors. Reinterpreting the results in terms of the
standard Hofstadter spectrum calls for a mixture of g=1 (fermion) and g=2 exclusion whose physical meaning and properties require further elucidation. In this context we also obtain some unexpected Fibonacci sequences within the weights of the combinatorial factors
appearing in the counting of walks. (Joint work with Stéphane Ouvry and Alexios P. Polychronakos)
] [article ] 17/10/2023
Pierre-Louis Giscard Dénombrement des polygones auto-évitants: la route déterministe [Slides.pdf ]abstract.htmlDepuis plus de 70 ans maintenant, le problème du dénombrement des polygones auto-évitants sur les réseaux réguliers du plan résiste aux efforts des mathématiciens. Pour poser ce problème, considérons un graphe planaire infini dont tous les nœuds sont identiques,
comme le réseau carré. On fixe un noeud sur ce graphe et on considère toutes les trajectoires sur le graphe partant de ce nœud et revenant à celui-ci en dernière étape et ne repassant jamais deux fois par le même nœud: on obtient un polygone auto-évitant (SAP en
anglais), la question étant de compter asymptotiquement les SAP de grande longueur. Les SAP apparaissent naturellement dans de nombreux processus aléatoires que nous présenterons brièvement. De fait, dénombrer les SAP a été quasiment exclusivement tenté à l'aide
d'argument probabilistes, culminants dans la loi de Schramm-Loewner (SLE_k) pour laquelle on conjecture que SLE_8/3 reproduit la loi uniforme sur les SAP. Parallèlement à ces développements, une route purement déterministe dans l'études des SAP a lentement émergé,
ceux-ci satisfaisant une extension semi-commutative de la théorie des nombres sur les monoids de Cartier-Foata. Dans cette extension, dénombrer les SAP revient à étendre le théorème des nombres premiers. Nous présenterons cette voie déterministe et en particulier
comment des cribles de la théorie des nombres permettent de s'approcher du but, offrant au passage la première méthode générique pour évaluer les valeurs concrètement prises par la loi de probabilité SLE_2 sur les SAP et de nouvelles indications sur les chemins
presque totalement auto-évitants.
] [article ] [vidéo ] 10/10/2023
Journée de rentrée du LIPNabstract.html
] 03/10/2023
Lionel Pournin Results on the volume of hypercube sectionsabstract.htmlIt is known that the largest possible volume for the intersection of a d-dimensional unit hypercube with a hyperplane H through its center is the square root of 2. This happens when H is orthogonal to a diagonal of a square face of the hypercube. This question can be generalized by considering the hyperplanes H at a fixed distance t to the center of the hypercube. Vitali Milman asked which among these hyperplanes have an intersection of maximal volume with the hypercube and conjectured that this happens when H is orthogonal to a diagonal or a sub-diagonal of the hypercube, depending on the value of t. Several recent results on this question are presented in this talk. In particular, when t is large enough (and smaller than the circumradius of the hypercube), the maximal volume is achieved exactly when the hyperplane is orthogonal to a diagonal of the hypercube. For smaller values of t, local extremality results will be presented at the diagonals and sub-diagonals of the hypercube.
] 26/09/2023
Sergio Cabello Barrier resilience problems and crossing numbers of graphs [Slides.pdf ]abstract.htmlIn an effort to provide breadth instead of going deep into a single topic, the talk will cover two sets of geometric problems that are unrelated and suitable for a general audience interested in discrete mathematics and algorithms.
In the first part I will explain variants of the barrier resilience problem, where the aim is to go from a source point to a target point in the plane visiting as few monitored regions as possible.
The problem appears in sensor networks and in robotics, and its solution is related to vertex-disjoint paths/cycles in graphs.
In the second part I will talk about crossing numbers of graphs and what we know about the crossing number of planar graphs with an additional edge.
] [vidéo ] 19/09/2023
Khaydar Nurligareev Asymptotics for graphically divergent series [Slides.pdf ]abstract.htmlWe propose a new method for obtaining the coefficients of complete asymptotic
expansions in a systematic manner, which is suitable for various families of
graphs in dense regime. The core idea is to introduce a new type of (bivariate)
generating series for the expansion coefficients, which we call a coefficient
generating function. We show that the coefficient generating functions
possess certain general properties that make it possible to express the
asymptotics in a short closed form and give a combinatorial meaning to their
coefficients. Applications of our method include asymptotics of connected
graphs, irreducible tournaments, strongly connected digraphs, satisfiable 2-SAT
formulae and contradictory strongly connected implication digraphs. Moreover,
using marking variables, we obtain asymptotics of the above families with a
fixed number of connected, irreducible, strongly connected and contradictory
components, respectively. This is joint work with Sergey Dovgal.
] [vidéo ] 20/06/2023
Boris Eng Jean-Yves Girard's transcendental syntax, linear logic and geometry of interaction (soutenance de thèse, équipe LoVE) 13/06/2023
Linxao Chen Transfer theorems for multivariate generating functionsabstract.htmlA multivariate generating function (MGF) is an analytic function in d variables ($d>1$) which encodes a d-dimensional array of numbers as its Taylor coefficients. In recent years we see the emergence of a theory of analytic combinatorics in several variables which
enables us to compute the asymptotic expansions of an array of numbers from its MGF. I will illustrate this theory with some examples from graph enumeration problems, and explain the new challenges it brings up compared to analytic combinatorics in one variable.
] [vidéo ] 13/06/2023
Sofia Tarricone La distribution de Tracy-Widom pour GUE et ses généralisationsabstract.htmlDans le modèle des partitions aléatoires considérées avec la mesure de Plancherel Poissonisée, la distribution de probabilité de la premiere partie d'une partition s'écrit en termes de déterminants de Toeplitz et elle se comporte, dans une certaine limite,
précisément comme la distribution de Tracy-Widom pour GUE (Baik-Deift-Johansson). Le premier objectif de cet exposé est donc de comprendre ces résultats et le deuxième est d'explorer leur généralisations pour d'autres modèles de partitions aléatoires, avant et après limite.
] [vidéo ] 13/06/2023
Cyril Banderier Phase transitions of composition schemes: Mittag-Leffler and mixed Poisson distributionsabstract.htmlMultitudinous probabilistic and combinatorial objects are associated with generating functions satisfying a composition scheme $F(z)=G(H(z))$. The analysis becomes challenging when this scheme is critical (i.e., $G$ and $H$ are simultaneously singular). Motivated by
many examples (random mappings, planar maps, directed lattice paths), we consider a natural extension of this scheme, namely $F(z,u)=G(u H(z))M(z)$. We also consider a variant of this scheme, which allows us to
analyse the number of $H$-components of a given size in $F$. We prove that these two models lead to a rich world of limit laws, where~we identify the key rôle played by a new universal law: the three-parameter Mittag-Leffler distribution, which is essentially the
product of a beta and a Mittag-Leffler distribution. We also prove (double) phase transitions, additionally involving Boltzmann and mixed Poisson distributions, bringing a unified explanation of the associated thresholds. In all cases we obtain moment convergence
and local limit theorems.
We end with extensions of the critical composition scheme to a cycle scheme and to the multivariate case, leading to product distributions. Applications are presented for random walks, trees (supertrees of trees, increasingly labelled trees, preferential attachment
trees), triangular Pólya urns, and the Chinese restaurant process.
] [vidéo ] 13/06/2023
Igor Kortchemski Global freezingabstract.htmlTravail en collaboration avec Étienne Bellin, Arthur Blanc-Renaudie, Emmanuel Kammerer.
] [vidéo ] 13/06/2023
Journée MathStic "Combinatoire et proba" : Cyril Banderier , Igor Kortchemski , Sofia Tarricone , Linxao Chen 06/06/2023
Axel Kerinec Une histoire de lambda calcul et d'approximation (soutenance de thèse, équipe LOVE) 30/05/2023
Nathanaël Enriquez Menhirs dans des déserts poissonniens (séminaire de proba)abstract.htmlDans le but d'étudier la mosaïque de Voronoi de processus ponctuels aléatoires vides de points dans de grandes régions, nous nous intéressons à la mosaïque de Voronoi dans le plan tout entier, d'un processus ponctuel de Poisson d'intensité uniforme sur le demi plan
et d'intensité nulle dans son complémentaire. Dans le demi plan ne contenant pas de points, elle donne lieu à des cellules arbitrairement allongées dont nous decrirons la limite en loi après renormalisation convenable.
Travail en collaboration avec Pierre Calka et Yann Demichel.
] 30/05/2023
Nathalie Eisembaum Une relecture du théorème d'isomorphisme de Dynkin (séminaire de proba)abstract.htmlLe théorème d’isomorphisme de Dynkin ainsi que ses dérivées, sont des identités en loi reliant, pour la plupart, les temps locaux d’un processus de Markov à des processus permanentaux. Malgré leurs utilisations variées, elles demeurent des identités en loi sans
interpretation trajectorielle simple. Nous proposerons une nouvelle lecture de l’identité surnommée « second théorème de Ray-Knight généralisé » et du théorème d’isomorphisme de Sznitman.
] 23/05/2023
Gauthier Roussilhe La numérisation aide-t-elle à la transition écologique ? Efficacité, effets rebonds et faux amis (Séminaire Labos 1point5, 13h00-14h30) 16/05/2023
Pallavi Panda Strip deformations of decorated polygons [Slides.pdf ]abstract.htmlWe use the interior of the arc complex to parametrise all those deformations of an ideal polygon, with vertices decorated with horoballs, that uniformly
lengthen every edge and diagonal. This is done by using strip deformations, following the work of Danciger-Guéritaud-Kassel in Margulis spacetimes via the arc complex.
As a consequence we get that the interior of the arc complex is an open PL-manifold of dimension one less than that of the deformation space of the polygon.
] [article ] [vidéo ] 09/05/2023
Craig Kaplan An aperiodic monotile (One World Numeration Seminar)abstract.htmlA set of shapes is called aperiodic if the shapes admit tilings of the plane, but none that have translational symmetry. A longstanding open problem asks whether a set consisting of a single shape could be aperiodic; such a shape is known as an aperiodic monotile or
sometimes an "einstein". The recently discovered "hat" monotile settles this problem in two dimensions. In this talk I provide necessary background on aperiodicity and related topics in tiling theory, review the history of the search for for an aperiodic monotile,
and then discuss the hat and its mathematical properties.
] [article ] 02/05/2023
Gérard Duchamp Shotgun Seminar 18/04/2023
CALIN
collectif, rédaction du rapport Hcéres 18/04/2023
Éric Brunet Refined large deviation results for the rightmost position in a branching Brownian motion (séminaire de proba du LAGA)abstract.htmlThe rightmost particle in a branching Brownian motion at time $t$ is, with high
probability, around position $2t - 3/2 \ln t$. The probability that it lies
around position $c t$ with $c>2$ is exponentially small with time, with a rate
which is known since Chauvin Rouault (1989). We investigate the details of
these large deviations, using as a starting point an intriguing relation
between the quantity we consider and the median position of the rightmost
particle.
] 18/04/2023
Kirone Mallick Exact solutions for the Asymmetric Simple Exclusion Process (séminaire de proba du LAGA)abstract.htmlThe asymmetric simple exclusion process is a paradigm of stochastic interacting particles, that was invented to describe low-dimensional
transport with constraints. Thanks to its rich mathematical and combinatorial properties, exact solutions have been obtained for this system and have lead us to a better understanding of non-equilibrium statistical mechanics.
The aim of this talk is to review some results about this model, describe the methods involved and present some recent developments.
] 11/04/2023
Jihyeug Jang Negative moments of orthogonal polynomials [Slides.pdf ]abstract.htmlWe'll begin with a short survey on orthogonal polynomials and then we'll consider the following model.
If a sequence indexed by nonnegative integers satisfies a linear recurrence without constant terms,
one can extend the indices of the sequence to negative integers using the recurrence.
Recently, Cigler and Krattenthaler showed that the negative version of the number of bounded Dyck paths
is the number of bounded alternating sequences.
In this talk we present two methods to compute the negative versions of sequences related
to moments of orthogonal polynomials.
We give a combinatorial model for the negative version of the number of bounded Motzkin paths.
We also prove two conjectures of Cigler and Krattenthaler on reciprocity between determinants.
Joint work with Donghyun Kim, Jang Soo Kim, Minho Song, U-Keun Song.
] [article ] [vidéo ] 04/04/2023
Adrian Tanasa Asympotic expansions for random tensor models [Slides.pdf ]abstract.htmlCombinatorial Physics is now a well-established interdisciplinary domain where combinatorics and physics interact in both directions.
In this talk I will present how a particular problem in theoretical physics (namely the implementation of the so-called double scaling limit mechanism for various random tensor models) is successfully tackled using purely combinatorial methods.
] [vidéo ] 21/03/2023
Valentin Bonzom Structural properties and enumeration of PL-manifolds (Soutenance HDR)abstract.htmlPour cette soutenance, j'introduirai les cartes combinatoires et les triangulations dites colorées en dimensions supérieures à 2. En dimensions 3 et plus, j'expliquerai les difficultés à classifier et énumérer les
triangulations de variétés, y compris de la sphère. Les triangulations colorées offrent un cadre qui permet de représenter les triangulations comme des graphes aux arêtes colorées. Cela a permis de nombreuses avancées, et je donnerai notamment un théorème qui
caractérise les collages de 3-boules maximisant le nombre d'arêtes. Initialement guidé par la perspective de construire d'autres modèles pour l'énumération de variétés en dimension 3, je me suis intéressé aux équations satisfaites par les séries génératrices de
cartes. Je parlerai ici de la hiérarchie KP, connue notamment pour être à l'origine de magnifiques récurrences sur le nombre de cartes en fonction de la taille et du genre, et de sa généralisation aux cartes non-orientées.
La soutenance sera présentée devant le jury composé de
Bruno Benedetti (U. Florida, examinateur)
Olivier Bodini (LIPN, président)
Marthe Bonamy (LaBRI, examinatrice)
Mireille Bousquet-Mélou (LaBRI, rapportrice)
Éric Colin de Verdière (LIGM, examinateur)
Nabil Mustafa (LIPN, examinateur)
Gilles Schaeffer (LIX, rapporteur)
] [article ] 28/02/2023
Michael Drmota Subgraph statistics in series-parallel graphs (Online Applied Mathematics Seminar ) 28/02/2023
Alan Sokal Motion of zeros of polynomial solutions of the one-dimensional heat equation: A first-order Calogero-Moser system (Complex Analysis video seminar ) 28/02/2023
Patrick Teller Inverser la fonction de Sylvester (étude élémentaire) [abstract.pdf ] 14/02/2023
Nicolas Delporte On aspects of two-dimensional quantum gravity [Slides.pdf ]abstract.htmlAfter a brief overview of recent advances in 2d quantum gravity related to JT gravity (Jackiw–Teitelboim gravity), we will suggest a different approach that relies on self-overlapping curves. We will then see how the algorithmic and combinatorial
properties of those curves can be analysed numerically.
] [vidéo ] 14/02/2023
Nicolas Delporte A random walk approach to two dimensional quantum gravityabstract.htmlAfter a brief overview of recent advances in 2d quantum gravity related to JT gravity,
we will suggest a different approach that relies on self-overlapping curves.
] 08/02/2023
Joseph Ben Geloun Tensor field theories: renormalization, combinatorics and algebras (soutenance HDR)abstract.htmlThe advent of tensor models (TM) in physics (quantum gravity theory) has produced eminent results that put them at the center of discussions in the early 90s. TM generalize matrix models producing the famous random maps whose continuum limit is known as the Brownian
sphere. They therefore
define useful tools for understanding discrete and random geometries in dimension greater than or equal to 3 as well as their continuum limits. My research, during the last past years, focused on their extension in a field theoretic setting. We discover several
crucial features of these field theories, both at the mathematical and physical level, and for all results, combinatorics plays a pivotal role. Combinatorics indeed illustrates the fertile link between mathematical physics, algebra and computer science that this thesis reports.
Plan of the presentation:
Jury
] [vidéo ] 24/01/2023
Lionel Pournin Distance, strong convexity, flagness, and associahedraabstract.htmlOne can always transform a triangulation of a convex polygon into another by performing a sequence of edge flips, which amounts to follow a path in the graph G of the associahedron. The least number of flips required to do so is then a distance in that graph whose
estimation is instrumental in a variety of contexts, as for instance in computational biology, in computer science, or in algebraic topology. On the other hand, it is known that paths in G correspond to a certain kind of 3-dimensional triangulation. This talk is
about the recent proof that these 3-dimensional triangulations are flag when the corresponding path is a geodesic. This result, that provides a new powerful tool to study the geometry of G, can be thought of as a 3-dimensional analogue of a well-known strong
convexity property of G. Several consequences on the computation of distances in G and on strong convexity in related graphs will be discussed. This talk is based on joint work with Zili Wang (Dartmouth College).
] 17/01/2023
Wolfgang Steiner Shift spaces defined by lexicographic inequalities and unique double base expansions [Slides.pdf ]abstract.htmlBeta-expansions are generalisations of the usual decimal or binary expansions to real bases. Instead of taking powers of a single base, we use powers of two bases where the exponents depend on the choice of the (binary) digit sequence. We study the question when
such expansions are unique and give a characterisation of the pairs of bases that admit non-trivial unique expansions or even uncountably many unique expansions. This is directly related to the question when a binary shift defined by two lexicographic inequalities
is non-trivial or uncountable, and the characterisation is in terms of S-adic words, where S consists of the Sturmian substitutions and the Thue-Morse substitution. This is joint work with Vilmos Komornik and Yuru Zou.
] [article ] [vidéo ] 10/01/2023
Mehdi Naima Extending Brandes algorithm to improve betweenness centrality computation in temporal graphs with discrete and continuous time [Slides.pdf ]abstract.htmlBetweenness centrality has been a long subject of study in network science since it was introduced by Freeman in 1977. This centrality measure asses the importance of nodes in a graph, it has been used for example in social, biological and research collaboration networks. Moreover, betweenness centrality has been used in graph partitioning and community detection in the well-known Girvan-Newan algorithm.
A simple approach to compute betweenness centrality for all the nodes of a static graph is to use Floyd-Warshall algorithm that runs in $O(n^3)$.
Brandes in 2001 published an algorithm that runs in $O(nm + n^2 \ln n )$ on weighted graphs, it is still considered one of the best theoretical results on the question.
Betweenness centrality has also been extended to temporal graphs.
Temporal graphs have edges that bear labels according to the time of the interactions between the nodes.
Betweenness centrality has been extended to the temporal graph settings, and the notion of paths has been extended to temporal paths.
Recent results by Buss et al. and Rymar et al. extended Brandes algorithm to the temporal setting with a general algorithm running in $O(n^2mT^2)$, where $T$ is the number of time units.
Their results rise 2 questions, one is about the nature of temporal paths and the other considering the extension of Brandes algorithm to the temporal setting.
In the seminar we will discuss these issues and address them.
We will see that we are able to deploy Brandes algorithm to its full extent and improve the running time of these recent results to $O(nmT + n^2T \ln(nT))$.
We will also discuss how Brandes algorithm can also be generalized to stream graphs which are dynamic graphs with continuous time and dynamicity on the nodes
] [vidéo ] 03/01/2023
Nicolas Broutin Invasion percolation and scaling limits (Online Applied Mathematics Seminar)abstract.htmlI will explain how the exploration of graphs using Prim's algorithm, or invasion percolation, yields intuitive approaches to some scaling limits the classical multiplicative coalescent processes related to random graphs.
This work is based on joint work with J.-F. Marckert.
] 13/12/2022
Ikram Garfatta Vérification formelle de processus dans la Blockchain (soutenance de thèse LIPN) 06/12/2022
Rafik Aguech Exponential recursive trees: profile study [Slides.pdf ]abstract.htmlMany processes involving growing trees/graphs are adding a small amount of nodes/edges at each step.
Such models often exhibit statistics (like the degree distribution)
which are not compatible with the ones observed e.g. in social networks.
Is there a natural mathematical model which possess this fast growing rate feature?
To this aim, we consider a new family of trees (introduced by Mahmoud): the exponential recursive trees.
At each step, one adds (with probability $p$) a new child to each node of the tree.
In this talk, we establish typical properties concerning the evolution at time $n$ of such a tree:
its size, its number of leaves at depth $d$, its internal path length, its number of protected nodes.
Using martingale theory, we give results on average or in $L^1$ and some of the corresponding limit distributions
(characterized by their moments). We end with some open problems.
] [vidéo ] 06/12/2022
Linglong Yuan et Matteo d'Achille (exposés au LAGA à 10h et 11h)30/11/2022
CIP R-algèbres et leurs caractères 23/11/2022
Viviane Baladi Propriétés statistiques des billards dispersifs (colloquium du Laga) 23/11/2022
CIP 15/11/2022
Alexandros Singh A unified approach to the combinatorics of the lambda-calculus and maps: bijections and limit properties (soutenance de thèse)abstract.htmlIn this thesis we study rooted maps (graphs embedded on surfaces), the linear lambda-calculus, and their combinatorial interactions.
Building upon recent bijective connections between these two domains, we make use of a combination of techniques drawn from map theory,
logic, and combinatorics to study the structural properties of large random trivalent maps (both planar and of arbitrary genus) and linear lambda-terms, as well as that of various families of objects related to these. Some of the properties studied on maps of
arbitrary genus and their corresponding families of lambda-terms include:
- The number of loops and bridges in trivalent maps and of identity and closed subterms in closed linear lambda-terms.
- The number of unary vertices in (1,3)-valent maps and of free variables in open linear lambda-terms.
- The number of binary vertices in (2,3)-valent maps and of unused abstractions in closed affine lambda-terms.
- The number of occurences of various patterns in trivalent maps and in closed linear lambda-terms.
Using the last, we obtain a lower bound on the average number of steps required to normalise a closed linear lambda-term.
As for planar maps, we study various parameters analogous to the above. We also present a novel interpretation of a recurrence by Goulden
and Jackson for trivalent planar maps, based on the study of the planar lambda calculus.
*Composition of the jury*
] [article ] 15/11/2022
Hsien-Kuei Hwang Bell numbers in the Edo period, modern perspectives, and local limit theoremsabstract.html We examine and clarify in detail the contributions
of Yoshisuke Matsunaga (1694?–1744) to the computation of Bell numbers
in the eighteenth century (in the Edo period), providing
modern perspectives to some unknown materials that are by far the earliest
in the history of Bell numbers.
Later clarification and developments by Yoriyuki Arima (1714–1783),
and several new results such as the asymptotic distributions
(notably the corresponding local limit theorems) of a few closely related
sequences are also given.
Joint work with Xiaoling Dou and Chong-Yi Li.
] [article ] 09/11/2022
Gérard Duchamp Théorèmes de Gelfand pour la physique 08/11/2022
Martin Pépin Directed ordered acyclic graphs: enumeration, uniform sampling, and links with classical labelled DAGsabstract.htmlDirected Acyclic Graphs (DAGs) are directed graphs in which there is no path
from a vertex to itself.
DAGs are an omnipresent data structure in computer science and the problem
of counting the DAGs of given number of vertices has been solved in the 70's
by Robinson.
For keeping the density of such graphs under control, one needs to take its
number of edges into account too. But the adaptation of Robinson's enumeration
to achieve this leads to counting formulas based on the inclusion-exclusion
principle, inducing a high computational cost for the uniform random
sampling based on this formula.
I will present two contributions.
First the enumeration of a new class of DAGs, enriched with an independent
ordering of the children of each vertex, according to their numbers of
vertices and edges.
A constructive recursive counting formula is obtained (i.e. without using the
inclusion-exclusion principle) thanks to a new decomposition scheme.
Then I will show the applicability of the method by proposing a constructive
enumeration of Robinson's labelled DAGs, by vertices and edges, based on the
same approach. The consequence of having such a formula is that efficient
uniform random samplers can be derived for both models.
] 01/11/2022
Vu Dinh Lazard's elimination in presented Lie algebras [Slides.pdf ]abstract.htmlIn this talk, we generalize the classical Lazard’s
elimination on the free Lie algebra L_k(X) to a more general scheme,
namely quotients of Lazard’s eliminations.
This implies (for Lie algebras defined by generators and relations)
situations when the alphabet of generators can be partitioned in a way
compatible with the relations. In this case, our scheme provides
semidirect decompositions of these Lie algebras. As particular cases
we consider the Partially Commutative Lie algebras and Drinfeld-Kohno
Lie algebras for which our result provides decompositions of the Lie
algebras (of these two series) into direct sums of free Lie algebras.
As a result, we indicate how to construct combinatorial bases (of
these Lie algebras) and their dual bases.
Incidentally, we recover answers to Pr. Schützenberger’s questions about the
Partially Commutative Free Lie algebra.
] [vidéo ] 25/10/2022
[CIP-Complexités] État des lieux et organisation 20/10/2022
Khaydar Nurligareev Irréductibilité des objets combinatoires : probabilité asymptotique et interprétation (soutenance de thèse)abstract.htmlDe nombreuses structures combinatoires admettent, au sens large, une notion d’irréductibilité : les graphes peuvent être connexes, les permutations indécomposables, les polynômes irréductibles, etc. Dans cette thèse, nous nous intéressons à la probabilité qu'un tel objet pris au hasard soit irréductible, lorsque sa taille tend vers l'infini. On obtient des développements asymptotiques complets pour ces probabilités ; l'irréductibilité est comprise à travers les constructions combinatoires SET, SEQ et CYC dans le contexte de la méthode symbolique. Nous appliquons notre approche aux graphes connexes, aux tournois irréductibles, aux permutations indécomposables et aux couplages parfaits. En outre, nous établissons des asymptotiques pour plusieurs modèles de surfaces connexes comprenant les surfaces à petits carreaux, les cartes combinatoires et certains objets de dimension supérieure tels que les constellations et les modèles de tenseurs colorés. Nous montrons que les coefficients apparaissant dans ces asymptotiques sont entiers et qu'ils peuvent être interprétés comme des suites de comptage d'autres classes combinatoires « secondaires ». Par exemple, les graphes connexes conduisent aux tournois irréductibles, les surfaces à petits carreaux aux permutations indécomposables, les cartes combinatoires aux couplages parfaits indécomposables. De plus, nous obtenons certaines probabilités asymptotiques qu'un objet combinatoire aléatoire ait un nombre donné de composantes irréductibles. Passant de la méthode symbolique à la théorie des espèces, nous traitons également le modèle G(n,p) de Erdös–Rényi. Nous établissons également la probabilité qu'un graphe orienté aléatoire soit fortement connexe en utilisant une décomposition plus complexe qui implique des graphes acycliques orientés.
] 11/10/2022
Carole Porrier A general approach to Ammann bars for aperiodic tilingsabstract.htmlAmmann bars are formed by segments (decorations) on the tiles of a tiling such that forming straight lines with them while tiling forces non-periodicity.
Only a few cases are known, starting with Robert Ammann's observations on Penrose tiles, but there is no general explanation or construction.
We propose a general method for cut and project tilings based on the notion of subperiods and we illustrate it with an aperiodic set of 36 decorated prototiles related to what we called Cyrenaic tilings.
] [article ] 04/10/2022
François Ollivier Hungarian matching algorithm, tropical determinants and Jacobi's bound for differential systems [Slides.pdf ]abstract.htmlJacobi's bound is a sharp bound on the order of quasi-regular solutions of a differential system, always conjectural in the general case. It is expressed as the tropical determinant of the order matrix of the system. This result appears in posthumous manuscripts of
Jacobi, which seem to come from a large abandoned project, Phoronomia. These texts reduce complexity problems related to the computation of normal forms to combinatorial problems, solved by original methods that make Jacobi a precursor of graph theory and shortest
path problems.
] [article ] [article ] [vidéo ] 04/10/2022
Lucas Gerin (exposé au LAGA) 27/09/2022
Thomas Fernique et Daria Pchelina Conjecture de Kepler et variationsabstract.htmlLa conjecture de Kepler stipule que la façon d'empiler les oranges qui minimise l'espace entre les oranges est bien celle utilisée sur les marchés. On se propose ici de mentionner quelques jalons importants vers la preuve de cette conjecture, et de décrire les
principales idées de la preuve finalement apportée par Hales & Ferguson en 1998. Si le temps le permet, on parlera de quelques problèmes voisins toujours ouvertes (plusieurs disques ou sphères notamment).
] 20/09/2022
Wolfgang Mulzer Long alternating paths exist [Slides.pdf ]abstract.htmlLet $P$ be a set of $2n$ points in convex position, such that n points are colored red and n points are colored blue. A non-crossing alternating path on $P$ of length $L$ is a sequence $p_1, ..., p_L$ of $L$ points from $P$ so that (i) all points are pairwise distinct; (ii) any
two consecutive points $p_i, p_{i+1}$ have different colors; and (iii) any two segments $p_i p_{i+1}$ and $p_j p_{j+1}$ have disjoint relative interiors,
for $i \neq j$.
We show that there is an absolute constant $\epsilon > 0$, independent of $n$ and of the coloring, such that $P$ always admits a non-crossing alternating path of length at least $(1 + \epsilon)n$. The result is obtained through a slightly stronger statement: there always exists a
non-crossing bichromatic separated matching on at least $(1 + \epsilon)n$ points of $P$. This is a properly colored matching whose segments are pairwise disjoint and intersected by a common line. For both versions, this is the first improvement of the easily obtained lower
bound of $n$ by an additive term linear in $n$. The best known published upper bounds are asymptotically of order $4n/3 + o(n)$.
Based on joint work with Pavel Valtr.
] [article ] 13/09/2022
Zéphyr Salvy Random planar maps decomposed into blocks: a phase study [Slides.pdf ]abstract.htmlMaps come with different shapes, such as trees or triangulations with many more edges. Many classes of maps have been enumerated (2-connected maps, trees, quadrangulations...), notably by Tutte, and a phenomenon of universality has been demonstrated: for the
majority of them, the number of elements of size $n$ in the class has an asymptotic of the form $\kappa\, \rho^{-n} \, n^{-5/2}$, for a certain $\kappa$ and a certain $\rho$. Nevertheless, there are classes of ``degenerate'' maps whose behaviour is similar to that
of trees, and whose number of elements of size $n$ has an asymptotic of the form $\kappa\, \rho^{-n} \, n^{-3/2}$, as for example outerplanar maps. This dichotomy of behaviour is not only observed for enumeration, but also for metrics. Indeed, in the ``tree'' case,
the distance between two random vertices is in $\sqrt{n}$, against $n^{1/4}$ for uniform planar maps of size $n$. This work focuses on what happens between these two very different regimes. We highlight a model depending on a parameter $u \in \mathbb{R}^*_+$ which
exhibits the expected behaviours, and a transition between the two: depending on the position of $u$ with respect to $u_C$, the behaviour is that of one or the other universality class. More precisely, we observe a ``subcritical'' regime where the scale limit of the
maps is the Brownian map, a ``supercritical'' regime where it is the Brownian tree and finally a critical regime where it is the $3/2$ stable tree.
] [vidéo ] 21/06/2022
Aofa 2022 (20-24 juin 2022, Philadelphia & online)13/06/2022
Christophe Tollu Circuits arithmétiques, universalité du déterminant, complexité algébrique 31/05/2022
Hoang Ngoc Minh On the solutions of Knizhnik-Zamolodchikov differential equations by noncommutative Picard-Vessiot theory [Slides.pdf ]abstract.htmlIn this talk, using the algebraic combinatorics on noncommutative formal power series with holomorphic
coefficients and a Picard-Vessiot theory of noncommutative differential equations, we give a
recursive construction of solutions of the Knizhnik-Zamolodchikov equations satisfying asymptotic conditions.
] [vidéo ] [article ] 24/05/2022
Nicolas Broutin Arbre couvrant minimum: du discret au continu [Slides.pdf ]abstract.htmlOn s’intéresse à l’arbre couvrant de poids minimum d’un graphe complet dont les arêtes sont pondérées par des uniformes indépendantes. On sait que cet objet a une limite d’échelle en tant qu’espace métrique. Je montrerai en quoi des représentations discrètes exactes
basées sur l’utilisation conjointe des algorithmes de Prim et de Kruskal permettent d’ouvrir la voie vers une construction explicite de la limite. Travail en collaboration avec J.-F. Marckert.
] [vidéo ] 23/05/2022
Christophe Tollu Représentations déterminantales [vidéo ] 17/05/2022
Anna vanden Wyngaerd From Delta to Theta conjecturesabstract.htmlIn 2015, Haglund Remmel and Wilson proposed two conjectural combinatorial interpretations of a certain symmetric function involving a certain Delta operator, which acts diagonally on the MacDonald polynomials. These formulas generalise the shuffle conjecture
(Haglund, Haimal, Loehr, Remmel, Ulyanov 2002), now theorem (Carlsson, Mellit 2018). In this talk, we will first discuss some of the motivation and history of these famous problems. Then, we will talk about our new symmetric function operator Theta and their role in
the proof of one of the Delta conjectures and the formulation of a possible unified Delta conjecture.
(Based on joint works with Michele D'Adderio, Alessandro Iraci, Yvan Le Borgne, Marino Romero)
] [article ] [vidéo ] 10/05/2022
Yohan Hosten Somme des chiffres, théorème central limite et odomètre b-adiqueabstract.htmlPour un entier $b\ge 2$ fixé, on s'intéresse à la variation de la fonction somme-des-chiffres (en base $b$), notée $s$. Plus précisément, pour un entier $r\in\mathbb{N}$, on considère la fonction, définie sur $\mathbb{N}$, $\Delta^{(r)}(n):=s(n+r)-s(n)$ et aux
propriétés asymptotiques de celle-ci. Ces propriétés sont bien définies sur le groupe des entiers $b$-adiques. On se proposera de construire un espace de probabilités à partir de ce groupe et du système dynamique de l'odomètre. Ce sera l'occasion d'y introduire la
notion de Tours de Rokhlin. Sur cet espace de probabilités, on considérera $\Delta^{(r)}$ en tant que variable aléatoire. On énoncera alors quelques propriétés vérifiées par $\Delta^{(r)}$. En particulier, on donnera un énoncé de type TCL avec vitesse de convergence
généralisant un résultat de Emme et Hubert. (Article en commun avec Thierry de la Rue et Elise Janvresse)
] [article ] [vidéo ] 25/04/2022
Christophe Tollu Déterminant : combinatoire, complexité et variantes (Séminaire inaugural)abstract.html Titre : Déterminant : combinatoire, complexité et variantes. Intention : L'accent sera mis sur les caractérisations combinatoires du déterminant
et leur utilisation pour obtenir de bonnes bornes de complexité ; tout le
matériel sera réutilisé dans les séances suivantes.
] 29/03/2022
Journées du GDR IM (29 mars-1 avril)22/03/2022
Journées Aléa (CIRM, 21-25 mars)15/03/2022
AG du laboratoire, Palmes Académiques pour Brigitte Guéveneux, buffet (F001), tertulia CALIN 08/03/2022
Sébastien Martineau Percolation arithmétique : étude des propriétés statistiques des points visibles dans un réseau (exposé au LAGA)abstract.htmlUn sommet du réseau ${\mathbb Z}^d$ est dit visible depuis l'origine si
le segment de droite joignant l'origine à ce sommet intersecte le
réseau en exactement deux points (l'origine et le sommet lui-même).
] [article ] 01/03/2022
Journées Nationales de Calcul Formel (CIRM, 28 fév-4 mars)15/02/2022
Ali Charara Matinée LIPN/INS2I (9h-12h30)abstract.html le 15 février, nous aurons la visite d'Ali Charara, directeur de l'Institut des Sciences de l'Information et de leurs interaction (INS2I) du CNRS.
Ce sera l'occasion de lui présenter le LIPN et un échantillon des recherches qui y sont menées (cf programme ci-dessous)
Cette visite se clôturera par un déjeuner auquel tous les membres du LIPN sont conviés.
Les exposés se dérouleront en amphi B et le déjeuner en salle M100.
] 08/02/2022
Alexios Polychronakos Algebraic area enumeration for lattice paths [Slides.pdf ]abstract.htmlWe give a summary of recent progress on the algebraic area enumeration of closedpaths on planar lattices. Several connections are made with quantum mechanics andstatistical mechanics. Explicit combinatorial formulae are proposed which rely onsums labelled by the
multicompositions of the length of the paths.
] [article ] [vidéo ] 01/02/2022
Alantha Newman Voting algorithms for unique games on complete graphs [Slides.pdf ]abstract.htmlAn approximation algorithm for a Constraint Satisfaction Problem is
called robust if it outputs an assignment satisfying a
$(1 - f(\epsilon))$-fraction of the constraints on any $(1-\epsilon)$-satisfiable
instance, where the loss function $f$ is such that $f(\epsilon) \rightarrow 0$ as
$\epsilon \rightarrow 0$. Moreover, the runtime of the algorithm should not depend in any
way on $\epsilon$. We present such an algorithm for the
Unique Games Problem on complete graphs with $q$ labels. Specifically,
the loss function is $f(\epsilon) = (\epsilon + c_\epsilon \epsilon^2)$, where $c_\epsilon$ is a
constant depending on $\epsilon$ such that $\lim_{\epsilon \rightarrow 0} c_\epsilon = 16$. The
runtime of our algorithm is $O(qn^3)$ (with no dependence on $\epsilon$) and
can run in time $O(qn^2)$ using a randomized implementation with a
slightly larger constant $c_\epsilon$. Our algorithm is combinatorial and
uses voting to find an assignment. We prove NP-hardness (using a
randomized reduction) for Unique Games on complete graphs even in the
case where the constraints form a cyclic permutation, which is also
known as Min-Linear-Equations-mod-q on complete graphs.
This is joint work with Antoine Meot, Moritz Muehlenthaler and Arnaud de Mesmay.
] [article ] [vidéo ] 25/01/2022
Mehri Javanian Asymptotic Analysis of Exponential Trees (exposé online au TU Wien/Univ Wien Diskrete Mathematik seminar ) 25/01/2022
Bruce Sagan Rowmotion on fences [Slides.pdf ]abstract.htmlRowmotion is a group action on partially ordered sets which has received much attention of late in the dynamical algebraic combinatorics community.
In particular, various statistics on posets turn out to be homomesic with respect to row motion, that is, the statistic has the same average over any orbit.
A fence is a poset obtained from a sequence of chains by identifying maximal and minimal elements in an alternating fashion.
These posets are important in the theory of cluster algebras and $q$-analogues.
] [article ] [vidéo ] 11/01/2022
FPSAC 2021 (10-20 janvier 2022)17/12/2021
Collectif
Problèmes ouverts, énigmes... 07/12/2021
Vu Dinh About solutions of Knizhnik-Zamolodchikov equation for the cases n=3,4abstract.htmlIn this talk, we present a solution of KZ(3) in K3^Id and then asymptotic solutions of KZ(4).
We also review some important problems of iterated integrals and Chen series over a simply connected manifold.
This paves the way for finding all solutions of KZ(n), for n>2.
PS: Voici un lien expliquant certains aspects des équations KZ : https://en.wikipedia.org/wiki/Knizhnik-Zamolodchikov_equations
] 02/12/2021
Combinatorics and Arithmetic for Physics: special days (IHÉS, 30 nov 2-déc) [Slides.pdf ]23/11/2021
Lionel Pournin Primitive point packing: number theory and geometric combinatorics [Slides.pdf ]abstract.htmlA point from the grid ${\mathbb Z}^d$ is called primitive when its coordinates are relatively prime. In this talk we will examine the question of how many primitive points one can pick, whose first non-zero coordinate is positive, under the constraint that the largest
coordinate of their sum is at most a fixed number $k$. We will solve the question exactly for all $k$ and $d$. A number of connections with number theory, geometric combinatorics, and the theory of linear programming will be made explicit along the way.
] 19/11/2021
Gérard Duchamp CCRT[32] Categorical aspects of Lazard's elimination theorems: strange gradings [Slides.pdf ] 16/11/2021
Julien David Une nouvelle approche pour l'analyse d'algorithme en moyenne: le cas de l'entropie de Shannon [Slides.pdf ]abstract.htmlThe average-case analysis of algorithm is often an object of controversy.
Some would say that it is not a relevant information of the algorithm’s "true" efficiency as
it is often based on the uniform distribution over the inputs, which is not a good modelization
of real-world contexts. Others would reply that the same can be said about worst-case
analysis and that, in this regard, average case analysis is a non negligible additional
information when one has to choose between two algorithms to solve a problem.
In this presentation, we adopt the following point of view: the average case analysis of an
algorithm is relevant to predict the algorithm behavior in a real-world context if and
only if there exists a property (either on the distribution or the object), determining for
the algorithm efficiency, whose average value is approximately the same given the random
distribution under which the algorithm is studied and in the real-world context.
In this study, the "determining property" we consider is the Shannon entropy of probability
distributions.
We exhibit several random generators of "probability distributions with fixed entropy" and
perform an experimental and theoretical analysis of string matching algorithms.
We obtain a continuous function, which takes a Shannon entropy as an input and returns
the average complexity of the naive string matching algorithm.
Joint work with Olivier Bodini and Izabell Iskandar.
] [vidéo ] 09/11/2021
Jean Cardinal Efficient generation of elimination trees and Hamilton paths on graph associahedraabstract.htmlAn elimination tree for a connected graph $G$ is a rooted tree on the vertices of $G$ obtained by choosing a root x and recursing on the connected components of G−x to produce the subtrees of x. Elimination trees appear in many guises in computer science and discrete
mathematics, and they encode many interesting combinatorial objects, such as bitstrings, permutations and binary trees. We apply the recent Hartung-Hoang-Mütze-Williams combinatorial generation framework to elimination trees, and prove that all elimination trees for
a chordal graph $G$ can be generated by tree rotations using a simple greedy algorithm. This yields a short proof for the existence of Hamilton paths on graph associahedra of chordal graphs. Graph associahedra are a general class of high-dimensional polytopes
introduced by Carr, Devadoss, and Postnikov, whose vertices correspond to elimination trees and whose edges correspond to tree rotations. As special cases of our results, we recover several classical Gray codes for bitstrings, permutations and binary trees, and we
obtain a new Gray code for partial permutations.
This is a joint work with Arturo Merino (TU Berlin) and Torsten Mütze (U. Warwick), to be presented at SODA'22.
] [article ] 09/11/2021
Hoang Ngoc Minh On the solutions of Knizhnik-Zamolodchikov differential equations by noncommutative Picard-Vessiot theory 02/11/2021
Maple Conference (online, 2-5 nov. 2021)02/11/2021
Vu Dinh About solutions of Knizhnik-Zamolodchikov equation for the cases n=3,4 26/10/2021
Michael Drmota Universal asymptotics for positive catalytic equations [Slides.pdf ]abstract.htmlCatalytic equations appear in several combinatorial applications, most notably in the numeration of lattice path and in the enumeration of planar maps.
The main purpose of this paper is to show that the asymptotic estimate for the coefficients of the solutions of
(so-called) positive catalytic equations has a universal asymptotic behavior.
In particular, this provides a rationale why the number of maps of size n in various planar map classes grows asymptotically like $c.n^{−5/2}\gamma^n$,
for suitable positive constants $c$ and $\gamma$.
Essentially we have to distinguish between linear catalytic equations (where the subexponential growth is $n^{−3/2}$)
and non-linear catalytic equations (where we have $n^{−5/2}$ as in planar maps).
Furthermore we provide a quite general central limit theorem for parameters that can be encoded by catalytic functional equations,
even when they are not positive. Joint work with Marc Noy and Guan-Ru Yu.
] [article ] [vidéo ] 26/10/2021
Jérémie Bouttier Cutting planar maps into slices [Slides.pdf ]abstract.htmlThe study of maps (graphs embedded into surfaces) is a rich subject at
the crossroads of mathematics, computer science and theoretical physics.
In this talk I will review the slice decomposition of planar maps : it
started as a reformulation of some (by now) classical bijections between
planar maps and trees, but then evolved into a general framework
applicable to many families of maps and to their scaling limits. For
simplicity I will restrict to the easiest setting of bipartite maps with
controlled face degrees. I will explain how slice decomposition allows
to enumerate pointed rooted maps, then "cylinders" and "pairs of pants"
(planar maps with two and three boundaries, respectively). The talk is
based on joint works with Emmanuel Guitter and Grégory Miermont.
] [article ] [vidéo ] 26/10/2021
Samantha Fairchild Counting tuples of closed geodesics on translation surfaces [Slides.pdf ]abstract.htmlWe will first introduce translation surfaces, which are Riemann surfaces built from gluing polygons in the plane via translations. The torus is the most basic example of a translation surface. The closed geodesics we count are called saddle connections, and are
found by following geodesics which start and end at a marked point. In the case of the torus, the saddle connections correspond to pairs of integers (a,b) which are coprime to each other. We will present probabilistic results counting saddle connections with length
conditions, as well as counting pairs of saddle connections with various pairing conditions. We will finish with highlighting the open questions and difficulties of counting triples of closed geodesics.
] [article ] [vidéo ] 26/10/2021
Cyril Marzouk On the geometry of biconditioned random trees [Slides.pdf ]abstract.htmlWe consider simply generated random plane trees with $n$ vertices and $k_n$ leaves, sampled from a sequence of weights. Motivated by questions on random planar maps, we will focus on the asymptotic behaviour of the largest degree. Precisely we will give conditions
on both the number of leaves and the weight sequence that ensure the convergence in distribution of the associated Łukasiewicz path (or depth-first walk) to the Brownian excursion. This should also provide a first step towards the convergence of the height or
contour function of the trees. The proof scheme is to reduce step by step to simpler and simpler objects and we will discuss excursion and bridge paths, non decreasing paths conditioned by their tip, and finally estimates of the form of the local limit theorem which
may be of independent interest.
Based on a joint work with Igor Kortchemski.
] [article ] [vidéo ] 26/10/2021
Benedikt Stufler Local convergence of random planar graphs [Slides.pdf ]abstract.htmlThe study of random combinatorial structures and their limits
is a growing field at the interface of combinatorics, probability
theory, and mathematical physics. Planar graphs are a prominent example
of such structures, yet important problems concerning their asymptotic
shape remain open. This talk highlights open conjectures and reviews
recent results, in particular the discovery of a Uniform Infinite Planar
Graph (UIPG) as their quenched local limit.
] [article ] [vidéo ] 26/10/2021
Journée MathStic "Combinatoire et Probabilités" (Jérémie Bouttier , Michael Drmota , Samantha Fairchild , Cyril Marzouk , Benedikt Stufler ) 19/10/2021
Veronika Pillwein On a sequence of polynomials generated by a Kapteyn series of the second kind (exposé à la journée du séminaire différentiel ) 19/10/2021
Hoang Ngoc Minh On the solutions of KZn with asymptotic conditions III 19/10/2021
Journées MathStic "Signaux biomédicaux : traitement et analyse mathématique" 12/10/2021
Imre Bárány Cells in the box and a hyperplane [Slides.pdf ]abstract.htmlIt is well known that a line can intersect at most $2n-1$ cells of the $n
\times n$ chessboard. What happens in higher dimensions: how many cells of the
$d$-dimensional $[0,n]^d$ box can a hyperplane intersect? We determine this
number asymptotically. We also prove the integer analogue of the following
fact. If $K,L$ are convex bodies in $R^d$ and $K \subset L$, then the surface
area $K$ is smaller than that of $L$. Joint work with Peter Frankl.
] [article ] 08/10/2021
Gérard Duchamp CCRT[31] Categorical aspects of Lazard's elimination theorems [Slides.pdf ]abstract.htmlSemi-direct products can be seen as solutions of universal problems
(see Andreas Thom's answer in MO96078 [1]) by means of
``structures acting on structures''.
On the other hand Lazard's elimination theorems (Lie groups, Lie algebras
and monoids) can be thought as byproducts of ``alphabets acting on codes''.
] 05/10/2021
Andrea Sportiello Boltzmann random generation of context-free grammars 05/10/2021
Hoang Ngoc Minh On the solutions of KZn with asymptotic conditions II 30/09/2021
Séminaire Flajolet (Marc Lelarge, Irène Marcovici, Valentin Féray) 28/09/2021
Philippe Marchal Urns in Lévy process (au Applied Mathematics Webinar of Jeddah-Riadh-Dammam-Tunis ) 28/09/2021
Joseph Ben Geloun Analyse asymptotique de l'énumération des invariants tensoriels de rang 3abstract.htmlConsidérons $n$ copies d'un tenseur complexe $T$ (de rang quelconque)
et $n$ copies de son complexe conjugué ${\bar T}$, et procédons à la contraction
des tenseurs avec une métrique triviale (symbole de Kronecker)
en ne permettant que des contractions entre les $T$ et les ${\bar T}$.
On obtient ainsi un invariant unitaire que l'on appelle invariant tensoriel.
Les invariants tensoriels sont ainsi faits de contractions de tenseurs
et sont au cœur de théories des champs (en physique) dont ils représentent les
observables. Une question naturelle est: de combien de façon
non équivalentes peut-on contracter ces $2n$ tenseurs complexes ?
Une réponse à cette question a été fournie dans [AIHPD (2014) 1, 77-138],
comme étant un dénombrement d'orbites d'actions de groupes symétriques.
Je présenterai l'analyse asymptotique à grand $n$ d'une telle énumération pour des
invariants tensoriels complexes de rang 3. La série asymptotique fait apparaître
les nombres de Stirling de seconde espèce. La généralisation à tout rang
est conjecturée.
] 28/09/2021
Hoang Ngoc Minh On the solutions of KZn with asymptotic conditions 21/09/2021
Valentin Féray On random combinatorial structures: partitions, permutations and asymptotic normality (soutenance HDR) 14/09/2021
Nicholas Beaton Walks obeying two-step rules on the square latticeabstract.htmlLattice walks taking steps from a fixed step set, and staying within some region of the lattice (most prominently, a quarter plane) have occupied combinatorialists for the past few decades and produced a huge range of rich results, drawing on algebra, probability
theory, differential equations, and computational methods. I will discuss a new twist on this idea -- walks on the edges of the square lattice which obey two-step rules. These allow (or forbid) steps in a given direction to be followed by steps in another
direction. We classify these rules according to a number of criteria, and show how these properties affect their generating functions, asymptotic enumerations and limiting shapes, on the full lattice as well as the upper half plane. The situation in the quarter
plane is still very unclear, but I'll discuss some preliminary computational results.
] [article ] 03/09/2021
Gérard Duchamp CCRT[30] Universal aspects of semidirect products 13/08/2021
Gérard Duchamp CCRT[29] A theory of domains for hyper- and polylogarithms [Slides.pdf ] 30/07/2021
Gérard Duchamp CCRT[28] Presentations, adjunctions and transitivity [Slides.pdf ] 27/07/2021
Hoang Ngoc Minh KZn via universal differential equation II 23/07/2021
Gérard Duchamp CCRT[27] Colimits, coequalizers and presentations [Slides.pdf ] 20/07/2021
Hoang Ngoc Minh KZn via universal differential equation 13/07/2021
Vu Dinh Towards KZn (first part): Recoding KZ3 09/07/2021
Gérard Duchamp CCRT[26] Colimits and categorification (short communication) [Slides.pdf ] 07/07/2021
Victor Lutfalla Plans discrets substitutifs (soutenance de thèse)abstract.htmlBonjour à toutes et tous,
J'ai le plaisir de vous inviter à ma soutenance de thèse intitulée
"Plans discrets substitutifs" qui se déroulera le 7 juillet à 14h en
hybride.
La soutenance sera publique et se déroulera dans la salle de séminaire
du LIPN à Villetaneuse, mais le nombre de participants est limité par la
situation sanitaire et si vous souhaitez venir physiquement merci de me
contacter par retour de mail. Vous pourrez aussi assister à ma
soutenance à distance sur
https://bbb.lipn.univ-paris13.fr/b/lut-uwi-axf-cq1 .
En cas de problème avec le serveur bbb nous basculerons sur
https://rdv2.rendez-vous.renater.fr/soutenance-these-lutfalla-8zchf
(nous n'utiliserons ce lien de visio que en cas de problème avec le
serveur principal).
Je soutiendrai mes travaux devant le jury composé de :
*Résumé:*
Un pavage est un recouvrement du plan par des tuiles qui ne se
chevauchent pas. Nous nous intéressons principalement aux pavages dont
les tuiles sont des losanges unitaires et qui sont exacts c’est à dire
que si on prend deux tuiles dans le pavages soit elles ne se touchent
pas, soit elles on un unique sommet en commun, soit elles ont une arête
entière en commun.
Les substitutions sont des applications qui à chaque tuile associent un
ensemble de tuiles appelé motif (dont la forme est habituellement la
même que celle de la tuile initiale mais en plus grand), une
substitution peut être étendue aux pavages en l’appliquant à chaque
tuile séparément et en recollant les motifs obtenus. Les substitution
permettent de construire des pavages avec une forte structure hiérarchique.
Les plans discrets sont des pavages exacts par losanges unitaires avec
un nombre fini de directions d’arêtes n que l’on peut relever dans R^n
et qui lorsqu’on les relève approximent un plan. On dit aussi pavages
planaires pour plans discrets. Notons que les plans discrets sont une
version relâchée des pavages coupe-et-projections.
Dans cette thèse nous étudions principalement les pavages substitutifs
par losange relevés dans R^n . Nous prouvons que les pavages Sub Rosa ne
sont pas des plans discrets, les pavages Sub Rosa sont des pavages
substitutifs par losange avec symétrie rotationnelle d’ordre n qui ont
été définis par Jarkko Kari et Markus Rissanen et qui étaient de bons
candidats pour être des plans discrets.
Nous définissons une nouvelle famille de pavages que l’on appelle les
pavages Planar Rosa qui sont des plans discrets substitutifs avec
symétrie rotationnelle d’ordre n.
Nous étudions aussi la méthode de la multigrille qui permet de
construire des pavages coupe-et-projection. On utilise cette méthode
pour donner une construction explicite pour des pavages
coupe-et-projection par losanges avec symétrie rotationnelle globale
d’ordre n
*Abstract:*
A tiling is a covering of the plane by tiles which do not overlap. We
are mostly interested in edge-to-edge rhombus tilings, this means that
the tiles are unit rhombuses and any two tiles either do not intersect
at all, intersect on a single common vertex or along a full common edge.
Substitutions are applications that to each tile associate a patch of
tiles (which usually has the same shape as the original tile but
bigger), a substitution can be extended to tilings by applying it to
each tile and gluing the obtained patches together. Substitutions are a
way to grow and define tilings with a strong hierarchical structure.
Discrete planes are edge-to-edge rhombus tilings with finitely many
finitely many edge directions be lifted in R n and which approximate a
plane in R^n , such a tiling is also called planar. Note that discrete
planes are a relaxed version of cut-and-project tilings.
In this thesis we mostly study edge-to-edge substitution rhombus tilings
lifted in R^n . We prove that the Sub Rosa tilings are not discrete
planes, the Sub Rosa tilings are edge-to-edge substitution rhombus
tilings with n-fold rotational symmetry that were defined by Jarkko Kari
and Markus Rissanen and which were good candidates for being discrete
planes. We define a new family of tilings which we call the Planar Rosa
tilings which are subsitution discrete planes with n-fold rotational
symmetry.
We also study the multigrid method which is a construction for
cut-and-project tiling and we give an explicit construction for
cut-and-project rhombus tilings with global n-fold rotational symmetry.
] 29/06/2021
A.D. Bruno & A.B. Batkhin Level lines of a polynomial in the plane (part of Computer Algebra Conference , 28-29 juin 2021) [Slides.pdf ] 25/06/2021
Gérard Duchamp CCRT[25] Kleene stars in shuffle algebras II [Slides.pdf ] 21/06/2021
Lattice Path Conference (21-25 juin 2021)18/06/2021
Gérard Duchamp CCRT[24] On the rôle of local analysis in the computation of polylogarithms and harmonic sums II [Slides.pdf ] 14/06/2021
AofA 2021 (14-17 juin 2021)11/06/2021
Gérard Duchamp CCRT[23] On the rôle of local analysis in the computation of polylogarithms and harmonic sums I [Slides.pdf ] 04/06/2021
Gérard Duchamp CCRT[22] MRS and the outer world III.1: PBW and rewriting techniques [Slides.pdf ] 03/06/2021
Séminaire Flajolet
Charlotte Hardouin, Kolja Knauer 03/06/2021
Journées ANR De rerum natura (3-4 juin) 31/05/2021
Journées GDR EFI (31 mai-2 juin) 31/05/2021
Journée MathStic
Mathematical aspects of covid-19 (Andrew Cairns, Aline Carneiro Viana, Laurent Dumas, David Sarrut, Chi Tran) 28/05/2021
Gérard Duchamp CCRT[22] MRS and the outer world III: m-adic topologies, holomorphic functional calculus and extensions [Slides.pdf ] 25/05/2021
CALIN tertulia CALIN 21/05/2021
Gérard Duchamp CCRT[21] MRS and the outer world II: Infinite sums as operators [Slides.pdf ] 18/05/2021
CALIN réunion d'équipe, puis tertulia CALIN 18/05/2021
Vu Dinh Monodromy representations of the braid groups in the case of a non-exceptional simple Lie algebra and its vector representation 14/05/2021
Gérard Duchamp CCRT[20] MRS and the outer world I [Slides.pdf ] 11/05/2021
Alexander Gnedin Online selection of long increasing subsequences and related problems (joint seminar with LAGA) [Slides.pdf ]abstract.htmlThe maximum expected length of increasing subsequence chosen by a real-time player from a random iid sequence is $\sqrt{2n}$, as was found by Samuels and Steele in 1981. In this talk we survey refinements and generalisations of this benchmark, also in connection with some bin-packing models.We further present recent results on fluctuations of the length and shape of the sequence selected by the optimal or a near-optimal policy.
] [vidéo ] 07/05/2021
Gérard Duchamp CCRT[19] Functional and Topological Questions I (Local domains) [Slides.pdf ] 04/05/2021
Ali Akhavi Modélisation des algorithmes et recherche de bornes inférieures de complexité pour les problèmes [Slides.pdf ]abstract.htmlNous introduisons une classe de problèmes appelés recherche de représentant. Étant donné un groupe G qui opère sur un ensemble X, l'entrée d'un problème sera un élément x de X et la sortie un représentant x* de l'orbite de l'orbite de x sous l'action de G. Nous
spécifions un rapport bien particulier entre X et G, qui permet, en utilisant le formalisme introduit par Gurevich pour modéliser les algorithmes, de dire que tout algorithme réversible
(dans le sens où toute donnée accessible au début d'une exécution est accessible jusqu'à la fin) résout en fait un tel problème.
Nous montrons que les traces d'exécution d'un tel algorithme est un diagramme (i.e., graphes orientés et arc-colorés) couvrant du diagramme de Cayley du groupe des automorphismes d'une algèbre naturellement associée à l'algorithme.
Notre approche permet de relier borne inférieure de complexité et diamètre d'un graphe de Cayley du groupe d'automorphisme, lorsque ce groupe est fini. Quand il est infini, mais à croissance polynomiale, notre approche fournit, sous une condition raisonnable, une
borne inférieure exponentielle, pour la complexité algébrique (i.e. on compte le nombre d'opérations élémentaires).
Si le temps le permet, nous parlerons également de la caractérisation du langage des traces d'exécution d'un algorithme.
] [vidéo ] 30/04/2021
Gérard Duchamp CCRT[18] Initial topologies, Dom(Li) and stars of the plane [Slides.pdf ] 27/04/2021
Stavros Garoufalidis Knots and their related q-series (séance jointe avec le webinaire EFI) [Slides.pdf ]abstract.htmlKnots give rise (via complex Chern-Simons theory) to matrices of q-series, (formal power series with integer coefficients) with
remarkable combinatorial, arithmetic and analytic properties, which define, in particular, holomorphic functions in the complex plane minus a ray. These are examples of 'holomorphic quantum modular forms'.
We will explain the main ideas with examples of the two simplest hyperbolic knots. Joint work with Rinat Kashaev, Don Zagier, Jie Gu and Marcos Marino (in various collaborations).
] [vidéo ] 23/04/2021
Gérard Duchamp CCRT[17] Towards a Wronskian-style (and cubeless) version of the BTT 20/04/2021
Cyril Banderier Pólya urns, the density method, and Young tableaux (séance jointe avec The Jeddah-Riadh-Dammam-Tunis Applied Mathematics Seminar) 20/04/2021
Hoang Ngoc Minh On universal differential equations (end + discussion) [Slides.pdf ] 16/04/2021
Gérard Duchamp CCRT[16] Higher order BTT, part three: One-parameter groups and identities among series [Slides.pdf ] 13/04/2021
Enrica Duchi Poissons combattants et arbres squelettesabstract.htmlEn 2016, avec Veronica Guerrini, Simone Rinaldi et Gilles Schaeffer,
(https://doi.org/10.1088/1751-8121/50/2/024002 et https://www.mat.univie.ac.at/~slc/wpapers/FPSAC2017/43%20Duchi%20Guerrini%20Rinaldi%20Schaeffer.pdf),
nous avons introduit un modèle de surfaces branchantes que nous avons appelées poissons combattants.
Ces poissons ont de belles propriétés énumératives encore largement mystérieuses : ils partagent la formule des cartes planaires non séparables enracinées,
mais une conjecture résiste, qui lie 4 paramètres de ces poissons à des paramètres des arbres ternaires gauches qui codent ces cartes.
En considérant le codage des poissons par leur arbre squelette, nous sommes récemment arrivé naturellement à une variante de ce modèle, qui se trouve avoir la même formule que les cartes planaires enracinées...
] [vidéo ] 13/04/2021
Hoang Ngoc Minh On universal differential equations VI [Slides.pdf ] 09/04/2021
Gérard Duchamp CCRT[16] Higher order BTT, part two: Asymptotic conditions and character properties [Slides.pdf ] 06/04/2021
Rémi Cocou Avohou A complete characterization of \((f_0, f_1)\)-pairs of 6-polytopes [Slides.pdf ]abstract.htmlWe discuss the characterization of $(f_0, f_1)$-pairs of $d$-polytopes for $d=3, 4, 5$. We completely characterize the $(f_0, f_1)$-pairs of $6$-dimension polytopes and find a characterization of $7$-dimension polytopes having excess degree greater than 11. We
finally conjecture bounds fulfilled by $d$-polytopes with excess greater than $3d-10$.
] [article ] [vidéo ] 06/04/2021
Hoang Ngoc Minh On universal differential equations V [Slides.pdf ] 02/04/2021
Gérard Duchamp CCRT[16] Higher order BTT, part one: localization [Slides.pdf ] 30/03/2021
Journée du séminaire différentiel (Masha Vlasenko, Duco van Straten, Jason Bell)30/03/2021
Hoang Ngoc Minh On universal differential equations IV [Slides.pdf ] 26/03/2021
Gérard Duchamp CCRT[15] Evolution equations in differential modules (unusual schedule due to the GDR-IM event) [Slides.pdf ] 23/03/2021
Journées du GDR IM (23-26 mars)23/03/2021
Hoang Ngoc Minh On universal differential equations III [Slides.pdf ] 19/03/2021
Gérard Duchamp CCRT[14] (Free?) differential calculus and automata theory 16/03/2021
Hoang Ngoc Minh On universal differential equations II [Slides.pdf ] 15/03/2021
Journées Aléa (15-19 mars)12/03/2021
Gérard Duchamp CCRT[12] Noncommutative gradings, language theory and free products (around MSE questions/625874) [Slides.pdf ] 09/03/2021
Julien Courtiel Solving Prellberg and Mortimer's conjecture - bijection(s) between Motzkin paths and triangular walksabstract.htmlEn ces temps difficiles, nous avons tous besoin de nous réconforter autour de jolies bijections pleines de couleurs.
Cet exposé parle d'un travail coréalisé avec Andrew Elvey-Price (Tours) et Irène Marcovici (Nancy). Nous avons répondu ensemble à une question ouverte de Mortimer et Prellberg, sollicitant une bijection entre une famille de marches dans un domaine triangulaire borné
(pensez à un grand triangle équilatéral subdivisé en plusieurs petits triangles équilatéraux) et les fameux chemins de Motzkin, mais avec une hauteur bornée.
Les techniques que nous utilisons pour les preuves sont élémentaires et semblent robustes. En plus de résoudre la conjecture de Mortimer et Prellberg, notre approche nous a permis de trouver une nouvelle bijection inattendue entre des marches tridimensionnelles
contraintes dans une pyramide et certaines marches bidimensionnelles sur une grille carrée.
] [article ] [vidéo ] 09/03/2021
Nicolas Behr Combinatorial evolution equations via rule-algebraic methodsabstract.htmlBuilding upon the rule-algebraic stochastic mechanics framework, I will present a new approach to computing multi-variate generating function expressions in combinatorics. This approach is applicable for combinatorial structures which can be described as some initial configuration together with a generator (ideally uniform) whose repeated applications render the structures of increasing sizes. Unlike in species theory, computations in this approach are based upon the notion of rewriting rules, their sequential compositions and the so-called rule algebras (which encode information on the combinatorics of sequences of rewriting steps). I will introduce a computational strategy for determining multi-variate generating functions describing joint distributions of pattern counts in a species, namely via a form of ODE system obtained from the computation of certain commutators (of rules in the generator with rules implementing pattern counts). Some concrete results for the species of planar rooted binary trees will be presented for illustration. I will put a particular emphasis on an interesting open problem which concerns the existence of the aforementioned type of combinatorial evolution equations as seen in the planar rooted binary trees example.
Reference: Nicolas Behr (2021). “On Stochastic Rewriting and Combinatorics via Rule-Algebraic Methods”. Invited Paper in Patrick Bahr (ed.): Proceedings 11th International Workshop on Computing with Terms and Graphs (TERMGRAPH 2020), Online, 5th July 2020, Electronic Proceedings in Theoretical Computer Science 334, pp. 11–28.
http://eptcs.web.cse.unsw.edu.au/paper.cgi?TERMGRAPH2020.2
] 05/03/2021
Gérard Duchamp CCRT[11] Partially commutative structures from a functorial point of view and Mélançon-Reutenauer-Schützenberger factorisations [Slides.pdf ] 02/03/2021
Elisa Gorla Complexity of Groebner bases computations and applications to cryptography (exposé online aux JNCF )abstract.htmlI will start from reviewing Groebner bases and their connection to polynomial system solving.
The problem of solving a polynomial system of equations
over a finite field has relevant applications to cryptography and coding theory.
For many of these applications, being able to estimate the complexity
of computing a Groebner basis is crucial. With these applications in mind,
I will review linear-algebra based algorithms, which are currently the most
efficient algorithms available to compute Groebner bases. I will define and
compare several invariants, that were introduced with the goal of providing
an estimate on the complexity of computing a Groebner basis, including the
solving degree, the degree of regularity, and the last fall degree.
Concrete examples will complement the theoretical discussion.
] 02/03/2021
Hoang Ngoc Minh On universal differential equations II 26/02/2021
Gérard Duchamp CCRT[10] Lie-theoretic aspects of noncommutative differential equations [Slides.pdf ] 23/02/2021
Samuele Giraudo Interstice operads of words [Slides.pdf ]abstract.htmlThe associative symmetric operad $As$ is the linear span of all permutations
endowed with an operation allowing us to insert a permutation into another one.
This structure is rich both under a combinatorial and an algebraic point of
view. In this context, Aguiar and Livernet have constructed alternative bases
of $As$ relating it with the combinatorics of the weak order on permutations.
In this talk, I will present a family of analogous operads, defined on some
families of words of integers. These operads are substructures of a master
structure called interstice operad. We obtain in this way operads on objects in
correspondence with permutations, increasing trees, Fuss-Catalan objects, or
walks in rectangles. One of the peculiarities of some of these operads is that,
despite to their relative simplicity, some are infinitely generated and have
nonquadratic and nonhomogeneous nontrivial relations.
Joint work with Camille Combe.
] [vidéo ] 23/02/2021
Hoang Ngoc Minh On universal differential equations [Slides.pdf ] 19/02/2021
Gérard Duchamp CCRT[9] Two noncommutative challenges (or recipes) [Slides.pdf ] 16/02/2021
Clément Dupont Théorie de Galois des périodes et des fonctions hypergéométriques de Lauricella (séminaire du GDR EFI) [Slides.pdf ] 16/02/2021
Gérard Duchamp Evolution, localisation and Wronskians [Slides.pdf ] 09/02/2021
Pierre Nicodème Sur l'article "Lindelöf representations and (non-)holonomic sequences" de Philippe Flajolet, Stefan Gerhold et Bruno Salvy [Slides.pdf ] [vidéo ] 09/02/2021
Gérard Duchamp About the arrow "can" (tensor product of series → double series, see MO questions 200442 and 201753), its usage in C.S. and combinatorics II [Slides.pdf ] 05/02/2021
Gérard Duchamp CCRT[8] Free structures without functors and free differential objects [Slides.pdf ] 02/02/2021
Gérard Duchamp Evolution equations and Picard-Vessiot theory I 01/02/2021
Journées de combinatoire de Bordeaux (1-5 février 2021)29/01/2021
Vu Dinh Towards a noncommutative Picard-Vessiot theory I 28/01/2021
Matěj Stehlik Postier chinois dans les triangulations planaires et applications à la chimie (séminaire AOC)abstract.htmlLe problème du postier chinois est un problème classique de l'optimisation combinatoire. Dans cet exposé, je me concentrerai sur le problème du postier chinois dans les triangulations planaires. Je montrerai une borne optimale sur la longueur du plus court parcours de postier, et je discuterai des liens à la chimie théorique.
] 26/01/2021
Ricardo Pérez Marco Produit de Hadamard, produit eñe et leurs formules de monodromie (séminaire du GDR EFI)abstract.htmlOn présentera le produit eñe, ses propriétés algébriques et analytiques, et son extension à des fonctions à singularités isolées.
Ceci conduit naturellement à la découverte des formules intégrales de la monodromie pour les produits eñe exponentiels et les produit de
Hadamard.
] [article ] [article ] [vidéo ] 26/01/2021
Hoang Ngoc Minh Lazard's elimination, Mélançon-Reutenauer-Schützenberger factorization and applications (2/2) [Slides.pdf ] 20/01/2021
Hoang Ngoc Minh Lazard's elimination, Mélançon-Reutenauer-Schützenberger factorization and applications (1/2) 19/01/2021
Nabil Mustafa Erdős-Szekeres theorem and three geometric applications of monotonic subsequences [Slides.pdf ]abstract.htmlGiven a sequence S of n real numbers, there always exists a monotonic subsequence of S of size sqrt(n). In this talk I will present three applications of this beautiful fact : conflict-free coloring (cellular networks), contact-maps (biology) and independent sets (graphs).
] [vidéo ] 19/01/2021
Gérard Duchamp Evolution observation: states and automata [Slides.pdf ] 14/01/2021
Joseph Ben Geloun CCRT[7] Linear automorphism group action on an *-algebra [Slides.pdf ] 12/01/2021
Irène Marcovici Corrélations discrètes d'ordre 2 de certaines suites automatiques [Slides.pdf ]abstract.htmlUne suite k-automatique est une suite qui peut être calculée par un automate fini de la manière suivante : le n-ième terme de la suite est fonction de l'état atteint
par l'automate après lecture de la représentation de l'entier $n$ en base $k$. Ces suites peuvent également être obtenues à partir du point fixe d'une substitution de longueur $k$.
Je montrerai qu'il existe des familles de suites automatiques qui, malgré leur description très simple, ont les mêmes corrélations d'ordre 2 qu'une suite i.i.d.
de symboles choisis uniformément au hasard. Plus précisément, pour tout entier $r>0$, et pour tout couple $(i,j)$ de symboles,
la proportion asymptotique d'entiers $n$ pour lesquels $(u_n,u_{n+r})=(i,j)$ est égale à $1/L^2$, où $L$ est le nombre de symboles.
La preuve repose sur des ingrédients simples et se généralise à des suites multi-dimensionnelles.
] [vidéo ] 12/01/2021
Gérard Duchamp About the arrow "can" (tensor product of series → double series, see MO questions 200442 and 201753), its usage in C.S. and combinatorics [Slides.pdf ] 08/01/2021
Gérard Duchamp CCRT[6] States, isometries, orbits and orthogonality in star-algebras [Slides.pdf ] 05/01/2021
Tertulia CALIN (open problems, puzzles) 05/01/2021
Gérard Duchamp Opening session: Deformations and coloured products [Slides.pdf ] 22/12/2020
Gérard Duchamp Closing session 18/12/2020
Mehdi Naima Combinatoire des arbres sous étiquetages croissants : asymptotiques, bijections et algorithmes (soutenance de thèse) [Slides.pdf ] [article ] 18/12/2020
Gérard Duchamp CCRT[5] Finite groups, states and semi-simplicity [Slides.pdf ] 15/12/2020
Tertulia CALIN 15/12/2020
Hoang Ngoc Minh Applications of Lazard's elimination [Slides.pdf ] 11/12/2020
Gérard Duchamp CCRT[4] Semi-simple categories of modules [Slides.pdf ] 08/12/2020
Tertulia CALIN 08/12/2020
Vu Dinh About (noncommutative) Picard-Vessiot theory 04/12/2020
Gérard Duchamp CCRT[3] Recap on universal problems and examples [Slides.pdf ] 03/12/2020
Journées SDA2 2020 : Systèmes Dynamiques, Automates & Algorithmes 01/12/2020
Philippe Duchon Analyse du pire cas probabiliste pour les quadtreesabstract.html Les quadtrees ("point quadtrees") sont un analogue multidimensionnel des arbres binaires de recherche, où un ensemble de points dans un espace de dimension d>1 sont représentés de manière hiérarchique par un arbre qui permet la recherche et l'insertion d'un
nouveau point en un temps contrôlé par la hauteur de l'arbre.
L'analyse probabiliste des quadtrees, réalisée dans les années 90 notamment par des méthodes analytiques, suppose généralement que les points sont pris aléatoirement (et uniformément) dans un domaine rectangulaire. Or, à la différence des arbres binaires de
recherche, il ne suffit pas de randomiser l'ordre d'insertion pour assurer que ce modèle est pertinent: la loi de l'arbre obtenu par insertion dans un ordre aléatoire de ces points dépend significativement du nuage de points considéré.
Nous montrons que, si l'on analyse la longueur de cheminement des arbres comme représentative du coût de construction du quadtree, on peut identifier exactement les pires nuages de points. C'est vrai en un sens probabiliste assez fort: la loi du cheminement total
pour le pire cas domine, pour l'ordre stochastique, la loi du cheminement pour tout autre nuage de points. En particulier, aucun nuage de points n'a une longueur de cheminement moyenne plus grande que le 2n log(n) des arbres binaires de recherche.
(Travail en commun avec Sophie Juppet)
Séminaire organisé par le LIGM.
] 01/12/2020
Hoang Ngoc Minh Factorisations à la Mélançon-Reutenauer-Schützenberger et applications [IV] [Slides.pdf ]abstract.htmlNous revoyons ensemble les étapes essentielles établissant l'équation faisant le pont entre les structures algébriques des polyzêtas convergent, via leur séries génératrices non commutatives mises sous forme factorisée MRS.
] 01/12/2020
Gérard Duchamp Kleene stars and shuffle algebras (4/4)abstract.htmlWe present some bialgebras and their monoid of characters. We entend the well-known theorem (when the scalars form a field) about linear independence of characters to the case of some rings. Examples of algebraic independence of subfamilies and identites derived from their groups (or monoids) of characters are provided. In this framework, we give a way to factorise characters (the MRS factorisation) as a resolution of unity as well as combinatorial counterparts of this resolution in terms of bases in duality.
] 27/11/2020
Gérard Duchamp CCRT[2] Universal problems, T=UL and applications [Slides.pdf ] 24/11/2020
Tertulia CALIN 24/11/2020
Hoang Ngoc Minh Factorisations à la Mélançon-Reutenauer-Schützenberger) et applications [III] [Slides.pdf ]abstract.htmlNous revoyons ensemble les étapes essentielles établissant l'équation faisant le pont entre les structures algébriques des polyzêtas convergent, via leur séries génératrices non commutatives mises sous forme factorisée MRS.
] 24/11/2020
Gérard Duchamp Kleene stars and shuffle algebras (3/4)abstract.htmlWe present some bialgebras and their monoid of characters. We entend the well-known theorem (when the scalars form a field) about linear independence of characters to the case of some rings. Examples of algebraic independence of subfamilies and identites derived from their groups (or monoids) of characters are provided. In this framework, we give a way to factorise characters (the MRS factorisation) as a resolution of unity as well as combinatorial counterparts of this resolution in terms of bases in duality.
] 20/11/2020
Gérard Duchamp CCRT[1] Universal problems, heteromorphisms, adjunctions and applications [Slides.pdf ] 17/11/2020
Daniel Vargas-Montoya Structure de Frobenius forte, algébricité modulo p et indépendance algébrique (Journée du séminaire différentiel ) 17/11/2020
Mioara Joldes On moment problems with holonomic functions (Journée du séminaire différentiel ) 17/11/2020
Tertulia CALIN 17/11/2020
Herwig Hauser Why don't we see C2 -singularities? (Journée du séminaire différentiel ) 17/11/2020
Hoang Ngoc Minh Factorisations à la Mélançon-Reutenauer-Schützenberger et applications [II] [Slides.pdf ]abstract.htmlNous revoyons ensemble les étapes essentielles établissant l'équation faisant le pont entre les structures algébriques des polyzêtas convergent, via leur séries génératrices non commutatives mises sous forme factorisée MRS.
] 16/11/2020
Journées graphes et algorithmes (16-18 novembre)13/11/2020
Gérard Duchamp Kleene stars in shuffle algebras (2/4) 10/11/2020
Hosam Mahmoud Pólya urns and Apollonian networkabstract.htmlWe briefly review a number of random networks in recent areas of interest of the speaker, and discuss the issues that arise. We present the Apollonian network as a case study. We study the distribution of the degrees of vertices as they age in the evolutionary
process. Asymptotically, the (suitably-scaled) degree of a node with a fixed label has a Mittag-Leffler-like limit distribution. The degrees of nodes of later ages have different asymptotic distributions, influenced by the time of their appearance. The very late
arrivals have a degenerate distribution. The result is obtained via triangular Pólya urns. Also, via the Bagchi-Pal urn, we show that the number of terminal nodes asymptotically follows a Gaussian law. We prove that the total weight of the network asymptotically
follows a Gaussian law, obtained via martingale methods. Similar results carry over to the sister structure of the k-trees.
[NB: For this talk, we have the pleasure to join the "Applied Mathematics Webinar", Jeddah - Riadh - Dammam - Tunis]
] 10/11/2020
Tertulia CALIN 10/11/2020
Gérard Duchamp Kleene stars in shuffle algebras (1/4) 05/11/2020
Journée opérades Samuele Giraudo, Guillaume Laplante-Anfossi, Maxime Lucas, Damiano Mazza 03/11/2020
Wissem Jedidi On complete monotonicity, Hausdorff 's moment characterization theorem and Mellin transform, with applications to infinite divisibility of probability measures [Slides.pdf ]abstract.html The class of completely monotone functions and Bernstein functions is important in the context of infinitely divisible probability measures of $(0,\infty)$. We shall provide for them several new characterizations via two approaches: the first one is driven
algebraically via elementary preserving mappings and the second one is developed in terms of the behavior of their restriction on $N$. As a consequence, we give a complete answer to the following question: "Can we affirm that a function $f$ is completely monotone
(resp. a Bernstein function) if we know that the sequence $(f (k))_k$ is completely monotone (resp. alternating)?". This approach constitutes a kind of converse to Hausdorff’s moment characterization theorem in the context of completely monotone sequences. With
closely related tools, we solve an open problem raised by Harkness and Shantaram (1969) who obtained, under sufficient conditions, a limit theorem in law for sequences of nonnegative random variables build with the iterated stationary excess operator. We show that
the conditions of Harkness and Shantaram are actually necessary; continuous time convergence is equivalent to discrete time convergence; and the only possible limits in distribution are mixture of exponential with log-normal distributions.
[NB: For this talk, we have the pleasure to join the "Applied Mathematics Webinar", Jeddah - Riadh - Dammam - Tunis]
] 03/11/2020
Hoang Ngoc Minh Factorisations à la Mélançon-Reutenauer-Schützenberger et applications [I] [Slides.pdf ]abstract.htmlNous revoyons ensemble les étapes essentielles établissant l'équation faisant le pont entre les structures algébriques des polyzêtas convergent, via leur séries génératrices non commutatives mises sous forme factorisée MRS.
] 27/10/2020
Joseph Ben Geloun Quantum mechanics of ribbon graphs: a combinatorial interpretation of the Kronecker coefficient as the dimension of a lattice [Slides.pdf ]abstract.htmlL'action de sous-groupes sur un produit de groupes symétriques permet d'énumérer différentes familles de graphes.
En particulier, les graphes à ruban bi-partis à $n$ arêtes (et au plus $2n$ sommets) sont les orbites de l'action adjointe
$( g s_1 g ^{-1} , g s_2 g ^{-1})$ dans $S_n \times S_n$,
où $g, s_1$ et $s_2$ sont des éléments de $S_n$.
Ces graphes forment une base d'une algèbre $K(n)$,
qui est aussi un espace de Hilbert pour un certain produit sesquilinéaire.
On y définit une famille finie d'opérateurs $T_i$,
qui commutent entre eux (système intégrable) et qui sont hermitiens.
Nous sommes donc en présence d'un modèle de mécanique quantique.
Dans une base de représentation de Fourier, étiquetée par les diagrammes de Young,
les $T_i$ admettent des valeurs propres
qui ne sont rien d'autre que les caractères (normalisés) de cette représentation.
On montre que les multiplicités des valeurs propres de ces opérateurs sont les coefficients de Kronecker, bien connus en théorie des représentations.
Nous démontrons qu'il existe un algorithme (HNF) de construction de cette multiplicité qui s'interprète
comme la dimension d'un sous-treillis du treillis des graphes à ruban :
$\mathbb{Z}^{{\rm Rib}(n)}$, où ${\rm Rib}(n)$ est le nombre de graphes à ruban bi-partis à n arêtes.
Ceci offre ainsi une réponse à la question de Murnaghan (Amer. J. Math, 1938)
sur l'interprétation combinatoire du coefficient de Kronecker.
Je finirai par une application au problème de décision
de l'annulation du coefficient de Kronecker.
] [vidéo ] 20/10/2020
Mehdi Naima Families of monotonic trees: combinatorial enumeration and asymptoticsabstract.htmlTBA!
] 20/10/2020
Gérard Duchamp Produits infinis (2/2)abstract.htmlLa théorie des produits infinis classiques s'inscrit naturellement dans celle des anneaux topologiques. Nous verrons en effet plusieurs exemples de convergences utilisés en combinatoire.
Puis quelques produits classiques seront passés en revue
Weierstrass
Newton-Girard
Produits unipotents
Factorisation MRS
] 13/10/2020
Cyril Banderier A random talk on random subjects from analytic combinatoricsabstract.htmlPublic will choose!
] 13/10/2020
Gérard Duchamp Produits infinis (1/2)abstract.htmlLa théorie des produits infinis classiques s'inscrit naturellement dans celle des anneaux topologiques. Nous verrons en effet plusieurs exemples de convergences utilisés en combinatoire.
Puis quelques produits classiques seront passés en revue
Weierstrass
Newton-Girard
Produits unipotents
Factorisation MRS
] 06/10/2020
Khaydar Nurligareev Asymptotics for the probability of labelled objects to be irreducible [Slides.pdf ]abstract.htmlThere are a number of combinatorial structures that admit a notion of irreducibility in some sense,
including connected graphs and surfaces, irreducible tournaments and indecomposable permutations. We are
interested in the asymptotic behaviour of probability that a random labelled object is irreducible, as its size
tends to infinity. It turns out that, under some conditions, it is possible to obtain this asymptotics with
the help of the symbolic method. Namely, it is so
when the considered combinatorial class can be described as a set or a sequence of the corresponding irreducible class,
and when its counting sequence grows sufficiently fast.
Moreover, the coefficients involved in the asymptotic expansion are often integers.
We explain their combinatorial meaning.
This is an ongoing joint work with Thierry Monteil.
] 06/10/2020
Alexandros Singh Distribution of parameters in certain fragments of the linear and planar λ-calculus [Slides.pdf ]abstract.htmlStructural properties of large random λ-terms may be gleaned by studying the asymptotic distributions
of various parameters of interest, such as the number of free variables, abstractions
and applications, and so on. Such properties have been studied for general λ-terms under
various considerations such as different notions of size and various structural restrictions.
Linear λ-terms, that is, terms where each variable occurs exactly once, form an interesting
subsystem of λ-calculus with various combinatorial connections to much-studied classes of
objects such as trivalent maps.
The purpose of this work is to help shed some light on what the “typical” terms of certain
fragments of the linear λ calculus look like. The fragments we deal with
in this work may be roughly partitioned into two major categories,
the algebraic and the differentially-algebraic one, according to the nature of the specifications they admit.
] 29/09/2020
Théophile Buffière Propriétés asymptotiques des zonotopes de dimension 2 et 3 [Slides.pdf ]abstract.htmlEn partant des travaux de O.Bodini sur les polyominos convexes, nous avons
écrit la construction combinatoire des zonotopes, et ainsi pu, avec les outils
de combinatoire analytique, obtenir le nombre asymptotique de zonotope dans un
carré de côté n, puis dans un cube de côté n, ainsi que d'autres propriétés
asymptotique tels le nombre de côté moyen, la forme limite.
Cette méthode est généralisable à toute dimension, mais devient très
fastidieuse en montant en dimension.
] 29/09/2020
Daria Pchelina Des empilements triangulés à trois disques qui maximisent la densité [Slides.pdf ]abstract.htmlQuels sont les empilements à trois disques les plus denses ? Un
empilement est dit triangulé si chacun de ses trous est borné par trois
disques tangents. Ces empilements semblent les meilleurs candidats
pour maximiser la densité. Il existe 164 paires $(r,s)$ tq $1>r>s$ permettant
un empilement triangulé par des disques de rayons $1$, $r$ et $s$. On est en
train de développer une méthode pour prouver que dans tous ces 164 cas
la densité est maximisée par un empilement triangulé.
] 15/09/2020
Thierry Monteil Codages de faible complexité de translations du tore T^dabstract.htmlUne façon d'apréhender un système dynamique $T:X\to X$ est de partitionner $X$
en un nombre fini de parties $P_i$ et d'associer à chaque point $x\in X$ un mot
infini qui décrit la suite des atomes de la partitions rencontrés le long de
l'orbite de $x$ par $T$. Ce codage symbolique permet, lorsque la partition est
convenable, de décrire les propriétés dynamiques de $T$ (mesures invariantes,
entropie, mélange, ...) en termes combinatoires (fréquences, complexité, ...).
La complexité du codage symbolique est la fonction qui associe à tout entier
$n$, le nombre de mots de longueur $n$ qui appraissent dans les mots infinis
obtenus. Cette notion raffine la notion d'entropie.
Étant donnée une translation $T$ du tore $\mathbb{T}^d$, nous pouvons essayer
de la coder de sorte à avoir une complexité la plus faible possible. Nous
verrons comment construire des partitions (dont le bord est nécéssairement
fractal) qui permettent d'obtenir une complexité linéaire.
Ce travail a été fait dans le cadre du groupe de travail Pytheas Fogg.
] [article ] 07/07/2020
Many online conferences:
Computability in Europe , Permutation Patterns , FPSAC (in July)...23/06/2020
Jim Propp Packings in one, two, and three dimensions: a macro-meso-microscopic view [Slides.pdf ]abstract.htmlHexagonal close-packings are the most efficient way to pack unit disks in R^2. But what do we mean by the definite article "the" in the previous sentence? Are hexagonal close-packings the only optimal packings? If we measure optimality by density, the answer is,
No. In fact, there are far too many density-optimal packings to classify in any meaningful way. This suggests that density is too coarse a notion to capture everything that we mean (or should mean!) by "efficient".
To study efficiency, we study deficiency, and seek ways to quantify defects in a regular packing. An obstacle here is that common kinds of defects inhabit disparate scales (e.g., point defects are infinitesimal compared to line defects, which in turn are
infinitesimal compared to the bulk). This suggests we turn to extensions of the real numbers that include infinitesimal elements (or rather, as turns out to be more helpful, infinite elements).
We use a regularization trick to make sense of these ideas (starting in one dimension). This enables us to sharpen our notion of optimal packing so that the optimal disk-packings are provably the hexagonal close-packings and no others. A side-benefit is a natural
but apparently new finitely additive, non-Archimedean measure in Euclidean n-space; it agrees with n-dimensional volume when applied to finite regions, but some infinite regions are "more infinite" than others.
For slides related to an earlier version of this talk, see http://jamespropp.org/brown18a.pdf
] [article ] [article ] [vidéo ] 23/06/2020
Camille Coron Démographie, extinction, et génétique des populations (séminaire organisé par l'équipe de proba)abstract.htmlLe but de cet exposé est de motiver, de construire, et d'étudier un modèle permettant d'analyser l'impact de la démographie et de l'extinction sur la composition génétique d'une population.
On considèrera une population d'individus diploïdes (c'est-à-dire qui possèdent deux versions de chaque gène)
caractérisés par leur génome à un locus multi-allélique (le vocabulaire biologique sera réintroduit en début d'exposé).
Cette population sera modélisée par un processus de diffusion stochastique obtenu comme limite d'échelle d'un processus de naissance et mort non-linéaire,
et qui peut être vu comme un processus de Wright-Fisher avec taille de population variable.
Ce processus limite permet d'étudier simultanément la composition génétique et la taille de la population
et notamment d'étudier la composition génétique de la population lors de l'extinction, dont le comportement sera relié à l'intégrabilité des trajectoires de l'inverse de la taille de population.
Certains comportements du modèle seront aussi comparés à ceux d'un modèle de Wright-Fisher classique.
] 16/06/2020
Piotr Śniady Poisson limit of bumping routes in the Robinson-Schensted correspondence [Slides.pdf ]abstract.htmlWe consider the Robinson-Schensted-Knuth algorithm applied to a random input and investigate the shape
of the bumping route (in the vicinity of the y-axis) when a specified number is inserted
into a large Plancherel-distributed tableau.
We show that after a projective change of the coordinate system the bumping
route converges in distribution to the Poisson process.
(Joint work of Łukasz Maślanka, Mikołaj Marciniak, Piotr Śniady).
] [article ] [vidéo ] 09/06/2020
Milica Tomasevic Particules en interaction singulière et non-markovienne pour Keller-Segel parabolique-parabolique (séminaire organisé par l'équipe de proba)abstract.htmlPour étudier le système de Keller-Segel dans sa forme parabolique, on propose un système de particules stochastique avec une interaction inhabituelle : chaque particule interagit avec le passé de toutes les autres par l’intermédiaire d'un noyau espace-temps
fortement singulier. On montrera l'existence et la propagation de chaos pour ce système dans le cas unidimensionnel. On discutera les résultats numériques dans le cas bi-dimensionnel et pourquoi les techniques de preuves développées en d=1 ne s’appliquent pas
ici. Nous énoncerons aussi un résultat d’existence et unicité pour l’EDS non-linéaire au sens de McKean sous des conditions explicites sur les paramètres du modèle dans le cas bi-dimensionnel.
] 02/06/2020
Igor Pak Counting with tiles [Slides.pdf ]abstract.htmlSay, you have a fixed set of tiles and want to count how many ways you can tile a rectangle of a fixed height, or a square. What kind of sequences can be obtained? This seeming innocent question is related to a number of beautiful problems in enumerative and
asymptotic combinatorics. I will give a broad overview of the subject and discuss the types of integer sequences that arise along the way. I will also mention a few curious conjectures.
] [vidéo ] 28/05/2020
Bruno Shapira Grandes déviations pour le nombre d'intersection de deux marches aléatoires (séminaire organisé par l'équipe de proba)abstract.htmlIl est bien connu que les traces de deux marches aléatoires simples indépendantes sur ${\mathbb Z}^d$ ont p.s. un nombre fini de points d’intersection si, et seulement si, $d > 4$. Dans cet exposé nous nous intéresserons à la queue de distribution de ce nombre de points
d’intersection en dimension 5 et plus. Je donnerai des éléments de preuve d’un résultat récent qui donne un principe de grandes déviations, et qui clôt - dans le cas discret - une question de van den Berg, Bolthausen et den Hollander datant de 2004.
] 19/05/2020
Colin Defant Stack-sorting, troupes, and 3-stack sortable permutationsabstract.htmlWest's stack-sorting map is a specific function that sends permutations to permutations.
I will discuss a certain Decomposition Lemma that has led to several advances in the understanding of this function, including a polynomial-time algorithm for counting 3-stack-sortable permutations.
We can generalize the Decomposition Lemma by considering special sets of binary plane trees called troupes.
I will also mention recent progress concerning the average number of iterations of the stack-sorting map needed to sort a permutation.
] [vidéo ] 12/05/2020
Florent Koechlin Weakly-unambiguous Parikh automata and their link to holonomic series [Slides.pdf ]abstract.htmlWe investigate the connection between properties of formal languages and properties of their generating series, with a focus on the class of holonomic power series.
It is a classical result that regular languages have rational generating series and that the generating series of unambiguous context-free languages are algebraic.
This connection between automata theory and analytic combinatorics has been successfully exploited. For instance, Flajolet used it in the eighties to prove the inherent
ambiguity of some context-free languages using criteria from complex analysis.
Settling a conjecture of Castiglione and Massazza, we establish an interesting link between unambiguous Parikh automata and holonomic power series,
which also yields characterizations of inherent ambiguity and algorithmic byproducts for these automata models.
This is a joint work with Alin Bostan, Arnaud Carayol and Cyril Nicaud.
] [vidéo ] 05/05/2020
Matěj Stehlik Combinatorial aspects of fullerenes and quadrangulations of surfaces [Slides.pdf ]abstract.htmlIn the first part of the talk, I will discuss some applications of graph theory to the study of fullerene molecules. In the second part, I will discuss how quadrangulations are related to Kneser graphs, and how they helped disprove two widely-believed conjectures in
commutative algebra.
] [vidéo ] 28/04/2020
Nabil Mustafa Sampling in combinatorial and geometric set systems [Slides.pdf ]abstract.htmlRandom sampling techniques have proven invaluable in constructing succinct approximations of large data sets, in particular those with geometric attributes in Euclidean spaces.
The study of such approximations involve several aspects: a better understanding of the
discrete and combinatorial structure of data in high dimensions, efficient algorithms for constructing succinct approximations,
the role and limits of random sampling, and applications of such approximations in algorithms and combinatorics.
] [vidéo ] 21/04/2020
Andrew Elvey Price Combinatorial functional equations and Jacobi theta function [Slides.pdf ]abstract.htmlI will discuss a fairly new method for solving certain systems of functional equations arising in combinatorics. I will start by describing the work of Bernardi, Bousquet-Mélou and Raschel on enumerating walks with small steps in the quarter plane, then I
will describe how I have applied this method more generally, in particular to counting certain walks by winding angle. In each case the solutions involve Jacobi theta functions.
] [vidéo ] 14/04/2020
Axel Bacher Exhaustive search of permutations with many patterns [Slides.pdf ]abstract.htmlHow many patterns (subsequences up to order isomorphism) of size k can a
permutation with size n contain? What are the optimal permutations? The
goal of this work is to answer this question experimentally, for n up
to 17, by exhaustively searching all permutations on GPUs. I will detail
the algorithms used, then do a quick introduction to GPU programming and
explain a few salient points of their implementation.
Work in common with Michael Engen (University of Florida).
] [vidéo ] 10/03/2020
Gérard Duchamp Identities between entire functions and their Hopf algebraic counterpart (1/2)abstract.htmlEuler's reflection identity between inverse Gamma functions (with center zero) suggest that there are symmetrisation procedures that amount to the lacunarization of the exponents in exponentials.
We start from, precisely, the lacunarization of the exponent in the Eulerian identity
$$
\dfrac1{\Gamma(1+z)}
=\exp\biggl(\gamma z-\sum_{n\ge2}\zeta(n)(-z)^n/n\biggr)
$$
and obtain, of course, a family of new entire function (with real coefficients).
] 05/03/2020
Rado Rakotonarivo On the combinatorics of lattice polytopes, random sampling and enumeration (soutenance de thèse)abstract.htmlThis thesis gathers several works on the lattice polytopes of IR^d. In particular, it focuses on the combinatorics of the family of the d-dimensional lattice polytopes contained in the [0,k]^d hypercube, denoted (d,k)-polytopes. Due to their elusive combinatorics,
a direct approach using the symbolic method is out of reach. Hence, we propose an original approach based on the description of a graph whose vertex set is the set of (d,k)-polytopes. In this graph, there is an edge between two polytopes if we can transform each of
them into the other by an elementary move. These elementary moves are local operations performed on the polytopes. Proceeding this way, we prove that the graph we defined is connected and we obtain a uniform random sampler based on a Markov Chain for the
(d,k)-polytopes of arbitrary dimension. We obtain also obtain two exhaustive enumeration algorithms.
The first part of this thesis focuses on the description of the above mentionned elementary moves and the study of the graphs based upon them. The second part presents the random sampling and the exhaustive enumeration algorithms.
Jury members: Anna Ben-Hamou,
Olivier Bodini,
Éric Colin de Verdière,
Jean-François Marckert,
Vincent Pilaud,
Mario Valencia-Pabon.
] 03/03/2020
Pascal Vanier Points apériodiques dans les espaces de pavage bidimensionnelsabstract.htmlLa théorie des espaces de pavages a été profondément façonnée par le
résultat historique de Berger : un jeu de tuiles fini peut ne paver le
plan que de manière apériodique. Ces points apériodiques sont au coeur
de nombreuses directions de recherche du domaine, en mathématiques comme
en informatique. Dans cette exposé, nous répondons aux questions
suivantes en dimension 2 :
1. Quelle est la complexité calculatoire de déterminer si un jeu de
tuiles (espace de type fini) possède un point apériodique ?
2. Comment se comportent les espaces de pavages ne possédant aucun point
apériodique ?
Nous montrons qu'un espace de pavage 2D sans point apériodique a une
structures très forte : il est "équivalent" (presque conjugué) à un
espace de pavage 1D, et ce résultat s'applique aux espaces de type fini
ou non. Nous en déduisons que le problème de posséder un point
apériodique est co-récursivement-énumérable-complet, et que la plupart
des propriétés et méthodes propres au cas 1D s'appliquent aux espaces 2D
sans point apériodiques. La situation en dimension supérieure semble
beaucoup moins claire.
Cet exposé est issu d'une collaboration avec Anael Grandjean et Benjamin
Hellouin de Menibus.
] 25/02/2020
Christian Lavault Structures libres et fonctions spéciales (collectif) 18/02/2020
Christian Lavault Mots, polynômes non commutatifs, monoïdes libres et algèbres libresabstract.htmlPlan
Introduction : un problème universel
Exemples de structures libres comme solutions de problèmes universels
L'algèbre $\frak{h} = K \langle X\rangle$ sur l'alphabet $X = \{0,1\}$, et ses deux sous-algèbres $\frak{h}^1$ et $\frak{h}^2$
Structure d'algèbres de shuffle et de stuffle, intégrales itérées des polylogs
Algèbres harmoniques, algèbre des séries formelles sur $X$ :
$K\langle \! \langle X\rangle \! \rangle$ et algèbre des séries rationnelles.
] 11/02/2020
Joseph Ben Geloun Ribbon graphs and the Bollobas-Riordan polynomialabstract.htmlWe will discuss ribbon graphs and their topological polynomial invariant that generalizes
the famous Tutte polynomial and that is called the Bollobas-Riordan (BR) polynomial.
After giving the definition of ribbon graphs and discussing their correspondence
with signed rotation systems, we will inspect the main topological properties of ribbon graphs
seen as surfaces with boundaries. We will then introduce the BR topological polynomial
invariant that satisfies a contraction-deletion recursion relation in a similar way of the Tutte polynomial.
If the time allows it, we may give a glimpse of the proof of the universality theorem for the BR polynomial.
] 04/02/2020
Gérard Duchamp Domains and a (new ?) family of entire functions IIabstract.htmlAfter having recalled and proved the set of "marvelous identities" evoked last week through
an Umbral coding of "the plane", we construct, after Minh's work, a regularized character
of the stuffle algebra which transports, point-by-point the Hausdorff group of the stuffle
algebra. We provide as well the $q$-analogue and set some open questions.
] 28/01/2020
Karol Penson Stieltjes moment problem: constructive approach towards unique and non-unique solutionsabstract.html
In this expository talk we present a constructive approach to generate exact solutions of the one-dimensional Stieltjes moment problem, with moments expressible via factorials and/or gamma functions. We will mainly concentrate on continuous solutions. The main
ingredient of this method is a systematic use of the inverse Mellin transform and of a generalization of hypergeometric function called the Meijer G function, fully implemented in computer algebra systems. The essential property inherent in these tools is the Mellin
(i.e. multiplicative) convolution. It allows one to produce exact solutions for a large family of various moment sets, especially those being combinatorial sequences. We enumerate various, older and more recent, criteria for positivity as well as for the uniqueness
of so obtained solutions. Our method permits one to bypass (in many cases) an involved question of verifications of these criteria. Amongst concrete examples reviewed here we mention the explicit construction of the so called Stieltjes classes of non-unique
solutions via polynomial killers, the problem of non-unique Lévy stable distributions and the construction of moment filters. Finally, a possible application of this methodology to purely discrete distributions will be briefly exposed.
] 28/01/2020
Gérard Duchamp One-parameter groups and combinatorial physicsabstract.htmlIn this talk, we consider the normal ordering of operators
of the type
$$
\Omega=\sum_{\alpha+\beta=r}c_{\alpha,\beta}(a^+)^\alpha a(a^+)^\beta,\ \ \alpha,\beta,r\textrm{ integers}
$$
where $a$ (resp. $a^{+}$) is a boson annihilation (resp. creation) operator;
these satisfy $[a,a^{+}]\equiv a a^{+}-a^{+}a=1$, and for the purposes of this presentation
may be thought of as $a\equiv d/dx$ and $a^{+}\equiv x$. We discuss the integration
of the one-parameter groups $e^{\lambda\Omega}$ and their combinatorial by-products.
In particular we show how these groups can be realized as groups of substitutions with
prefactor functions.
To end with, we provide a recent application of the concept one-parameter groups to
arithmetics.
] 21/01/2020
Thomas Fernique Densité des empilements de disquesabstract.htmlPour disposer des pièces d'un euro sur une table sans superposition de façon à laisser le moins de surface libre, la meilleure façon est de les centrer sur une grille triangulaire. La première preuve est due à Toth (1943), on en présentera une preuve élémentaire.
Peut-on faire plus dense si on a des pièces de un et deux euros ? Et si on peut jouer librement sur la taille des pièces ? On présentera quelques résultats et preuves, qui font intervenir des triangulations style Delaunay, de l'arithmétique d'intervalle et font travailler l'ordinateur. La morale est : à la fin, les pavages gagnent.
] 21/01/2020
Gérard Duchamp Commutative convergence, local domains and extensions of identities: Practical case studiesabstract.htmlThe question of extension of (partially defined) operators is ubiquitous
in mathematics, physics and computer science. Here, after having dealt with it in general,
we explicit concrete computations illustrating cases of unconditional and conditional convergences. This talk provides a collection of techniques coming from Mathematics, Computer Science and Arithmetics.
We to recall some of the facts about conc-characters ("Stars of the Plane") and the enlargement of indexations from polynomials to series (especially those who allow a "calculus" i.e. rational ones), from elements to shuffle and stuffle subalgebras.
Nuclearity of Hardy spaces
Examples of unconditional convergence, partition of indices for the transform of
$\frac{log(1+x_0)}{x_0}x_1$ and handling of the "magic identity".
References
In SLC 74 : (Pure) Transcendence Bases in φ-Deformed Shuffle Bialgebras (22 pp.) , SLC 74
G. H. E. Duchamp and C. Tollu, Sweedler's duals and Schützenberger's calculus , In K. Ebrahimi-Fard, M. Marcolli and W. van Suijlekom (eds), Combinatorics and Physics, p. 67 - 78, Amer. Math. Soc. (Contemporary Mathematics, vol.~539), 2011.
https://mathoverflow.net/questions/310354/independence-of-characters-with-respect-to-polynomials
G.H.E. Duchamp, Ngo Quoc Hoan, Hoang Ngoc Minh,
Kleene stars of the plane, polylogarithms and symmetries , TCS, 800 , 2019, 52-72,
] 14/01/2020
Matteo D'Achille Le problème de l'assignation aléatoire euclidienne : état de l'art et quelques résultats récents en dimension d=1abstract.htmlLe problème de l'assignation aléatoire euclidienne peut être considérée comme l'étude des propriétés statistiques de l'état fondamental d'un système dont les configurations sont constituées des matchings d’un graphe bipartite et dont les sommets sont extraits d'une
certaine mesure de probabilité supporté sur $\mathbb{R}^d$.
Ce problème est maintenant un problème classique dont les liens avec d'autres problèmes importants dans différentes disciplines sont bien connus depuis quelque temps. Après avoir discuté de certains de ces liens, je vais présenter une approche simple pour l'étude de
l'asymptotique du coût moyen de la solution optimale en dimension d=1 (travail avec Andrea Sportiello). Par cette méthode, je montrerai comment régions où la densité de probabilité associée aux sommets du graphe bipartite est faible peuvent donner lieu à des
corrections anomales à cette asymptotique (aussi logarithmiques), et comment, dans un autre cas, ces contributions peuvent être comparées à des contributions véritablement collectives par le biais de lignes critiques.
] 14/01/2020
Gérard Duchamp Algebraic and analytic extensions of the characters Li and H (3/3)abstract.htmlThe question of extension of (partially defined) operators is ubiquitous
in mathematics, physics and computer science. We will deal with it in general
and questions of renormalisation and regularisation of polyzetas, in particular
Algebraic independence of certain conc-characters ("Stars of the Plane").
Enlargement of indexations from polynomials to series (especially those who
allow a "calculus" i.e. rational ones).
Downsampling Wrench's formula.
References
In SLC 74 : (Pure) Transcendence Bases in φ-Deformed Shuffle Bialgebras (22 pp.) , SLC 74
G. H. E. Duchamp and C. Tollu, Sweedler's duals and Schützenberger's calculus , In K. Ebrahimi-Fard, M. Marcolli and W. van Suijlekom (eds), Combinatorics and Physics, p. 67 - 78, Amer. Math. Soc. (Contemporary Mathematics, vol.~539), 2011.
https://mathoverflow.net/questions/310354/independence-of-characters-with-respect-to-polynomials
G.H.E. Duchamp, Ngo Quoc Hoan, Hoang Ngoc Minh,
Kleene stars of the plane, polylogarithms and symmetries , TCS, 800 , 2019, 52-72,
] 07/01/2020
Jean Peyen Probabilistic approach of asymptotics of integer partitions [Slides.pdf ]abstract.htmlUsing a probabilistic approach proposed by Vershik, one can study various classes of integer partitions. By endowing those classes with the Boltzmann distribution and applying local limit theorems,
one may derive asymptotic enumeration formulas (such as the Hardy–Ramanujan formula), or the shape of partitions of large integers (e.g. the curve derived by Temperley in 1952).
After reminding some notions of combinatorics and the definition of the Boltzmann distribution over a combinatorial structure, we will explain a
procedure that can be used in order to derive the kind of results we mentioned and we will discuss applications to some classes of partitions.
] 07/01/2020
Gérard Duchamp Algebraic and analytic extensions of the characters Li and H (2/3)abstract.htmlThe question of extension of (partially defined) operators is ubiquitous
in mathematics, physics and computer science. We will deal with it in general
and questions of renormalisation and regularisation of polyzetas, in particular
Algebraic independence of certain conc-characters ("Stars of the Plane").
Enlargement of indexations from polynomials to series (especially those who
allow a "calculus" i.e. rational ones).
Downsampling Wrench's formula.
References
In SLC 74 : (Pure) Transcendence Bases in φ-Deformed Shuffle Bialgebras (22 pp.) , SLC 74
G. H. E. Duchamp and C. Tollu, Sweedler's duals and Schützenberger's calculus , In K. Ebrahimi-Fard, M. Marcolli and W. van Suijlekom (eds), Combinatorics and Physics, p. 67 - 78, Amer. Math. Soc. (Contemporary Mathematics, vol.~539), 2011.
https://mathoverflow.net/questions/310354/independence-of-characters-with-respect-to-polynomials
G.H.E. Duchamp, Ngo Quoc Hoan, Hoang Ngoc Minh,
Kleene stars of the plane, polylogarithms and symmetries , TCS, 800 , 2019, 52-72,
] 17/12/2019
Ilya Galanov Self-assembly of aperiodic tilings (Soutenance de thèse) 10/12/2019
Gérard Duchamp Algebraic and analytic extensions of the characters Li and H (1/3) 03/12/2019
Christian Bean Combinatorial exploration: an algorithmic approach to enumeration [Slides.pdf ]abstract.htmlPermutations, words, tableaux, and other such families of objects often play a role in diverse subfields of mathematics, physics and computer science.
When the structure of the object under investigation is known there are well-established tools,
such as symbolic and analytic combinatorics, that derive an enumeration, asymptotics, and the ability to randomly generate instances of the objects.
However, the initial step from a definition of the object to a structural description is often ad-hoc, human-staring-at-a-blackboard
type of work. We thus tried to automatize this work via an implementation "Combinatorial Exploration" in Python and applied it to
several combinatorial objects, such as permutations, set partitions and words.
In this talk we will focus on permutations and show how we have found structural descriptions of so-called 'permutation classes'.
(See the project webpage: https://permutatriangle.github.io/papers/2019-02-27-combex.html)
] [article ] 26/11/2019
Massimiliano Goldwurm Analysis of algorithms for membership problems on trace languages [Slides.pdf ]abstract.htmlA classical problem over trace monoids is the recognition of rational trace languages.
This problem can be solved in a time proportional to the number of prefixes of the input trace.
In this talk I will present some results on the number of prefixes of a trace of length n in the
worst case and in the average case under suitable probabilistic assumptions.
I will also discuss other results concerning the variance, the moments and the limit distribution of the
corresponding random variables.
] 26/11/2019
Christian Lavault Sur une erreur fructueuse de Paul Appell (4/4) 19/11/2019
Florent Hivert Expérimentations sur le calcul hautes performances en combinatoireabstract.htmlIn this talk, I will report on several experiments around large scale
enumerations in enumerative and algebraic combinatorics.
I'll describe a methodology used to achieve large speedups in several
enumeration problems. Indeed, in many combinatorial structures (permutations,
partitions, monomials, young tableaux), the data can be encoded as a small
sequence of small integers that can often efficiently be handled by a creative
use of processor vector instructions. Through the challenging example of
numerical monoids, I will then report on how Cilkplus allows for a extremely
fast parallelization of the enumeration. Indeed, we have been able to
enumerate sets with more that 10^15 elements on a single multicore machine.
En collaboration avec Jean Fromentin.
] 19/11/2019
Christian Lavault Sur une erreur fructueuse de Paul Appell (3/4) + Théorie des domaines (discussion) [abstract.pdf ] 12/11/2019
David Auger Un algorithme stochastique pour résoudre les jeux stochastique simplesabstract.htmlAprès avoir présenté des généralités concernant les jeux stochastiques simples (qui sont des chaînes de Markov où deux adversaires peuvent contrôler certains sommets), nous feront en particulier l'état en ce qui concerne les algorithmes de résolution de ces jeux, en regardant en particulier les algorithmes d'itération de stratégies. Enfin, nous présenterons un algorithme stochastique, qui améliore l'état de l'art, ayant une complexité paramétrée par le nombre de nœuds aléatoires du graphe.
] 12/11/2019
Christian Lavault Sur une erreur fructueuse de Paul Appell (2/4) [abstract.pdf ] 06/11/2019
Journées "Combinatorics and Arithmetic for Physics" (IHP, 6-8 novembre)05/11/2019
Vonjy Rasendrahasina On the sparse random acyclic digraphsabstract.htmlIn this talk, we consider the probability space of random digraphs defined as
follow. We generate a random undirected graph by taking the
classical Erdős–Rényi model $\mathbb G(n,p)$. Thereafter, each
edge is given a direction, where each of the two directions has
probability $\frac{1}{2}$ and all choices are made independently. The
result is a simple digraph on $n$ vertices. We will study the the
probability that a random digraph is acyclic when $p=O(1/n)$, i.e. it does not contain
a directed cycle when the number of edges is linear in the number
of vertices. This is a joint work with Dimbinaina Ralaivaosaona and
Stephan Wagner.
] 05/11/2019
Gérard Duchamp A localization principle for the Basic Triangle Theorem 29/10/2019
Pierre-Yves Bienvenu The Green-Tao theorem and polynomial configurations in the primesabstract.htmlGreen and Tao famously proved that the set of primes contains arbitrarily long arithmetic progressions. We will explain the heavy machinery behind the Green-Tao theorem and explains why polynomial configurations are much harder than linear ones and what can still be
done for them. We will also discuss other extensions of the Green-Tao theorem.
] [article ] 29/10/2019
Hoang Ngoc Minh Towards a noncommutative Picard-Vessiot theory (with simple applications)abstract.htmlWe are constructing the first steps of a noncommutative Picard-Vessiot theory and we
illustrate this theory in the study of independences of a new family of Gamma functions.
] 23/10/2019
Alexander Iksanov Functional limit theorems for divergent perpetuities and Galton-Watson processes with very active immigrationabstract.htmlI am going to discuss weak convergence in the Skorokhod space of Galton-Watson processes with immigration (GWI), properly normalized, under the assumption that the tail of the immigration distribution has a logarithmic decay. It will be explained that the limits are
extremal shot noise processes. Interestingly, both the behavior in mean and the survival probability (especially in the subcritical case) of the underlying Galton-Watson processes without immigration affect the asymptotics in question.
The sequence of the conditional expectations of GWI given the immigration forms a very particular instance of a (divergent) perpetuity. In view of this I shall also present functional limit theorems in the Skorokhod space for general divergent perpetuities and
suprema of perturbed random walks which are closely related objects.
] 23/10/2019
Dariusz Buraczewski Large deviations for random walk in random environmentabstract.htmlIn this talk we will discuss recent results concerning large deviations of one-dimensional nearest neighbour random walk in site-random environment. Our main contribution is an extension of large deviation results to precise (rather than logarithmic) asymptotic. We
will explain how this result is related to large deviations of branching process in random environment and stochastic recurrence equations.
] 23/10/2019
Jean-Baptiste Gouéré Non percolation dans des graphes géométriques orientés de degré sortant égal à 1abstract.htmlConsidérons un processus de Poisson ponctuel dans le plan. À l'instant initial, un segment issu de chaque point de ce processus croît à une vitesse aléatoire dans une direction aléatoire. La croissance de ce segment s'arrête dès qu'il en touche un autre. La réunion
des segments percole-t-elle ? Quel est le lien avec le titre de l'exposé ? Travail en collaboration avec David Coupier et David Dereudre.
] 22/10/2019
Vincent Beffara Box crossing for 2D models without Fortuin-Kasteleyn-Ginibre 22/10/2019
Andrea Sportiello The tangent method for the determination of Arctic curves: the simplest rigorous applicationabstract.htmlIn the paper Arctic curves of the six-vertex model on generic domains: the Tangent Method [J. Stat. Phys. 164 (2016), arXiv:1605.01388], of Filippo Colomo and myself, we pose the basis for a method aimed at the determination of the ``arctic curve'' of large random
combinatorial structures, i.e. the boundary between regions with zero and non-zero local entropy, in the scaling limit.
In this paper many things are claimed, and few are proven. In particular, it is not made clear that variants of it can be made fully rigorous in certain circumstances. In this seminar we present the simplest such instance: we rederive the arctic circle phenomenon
for ``domino tilings of the aztec diamond'', first discovered by Jockusch, Propp and Shor [arXiv:math/9801068, but in fact from 1995].
] 22/10/2019
Sergey Dovgal The subcritical phases of random structuresabstract.htmlWe will discuss the emerging substructures in graphs with degree constraints, digraphs, acyclic digraphs, and 2-CNF below the point of their respective phase transitions. While long time ago, probabilistic method allowed to establish the location of the transition
points, with some very rough properties, more and more refined results gradually become available. With analytic combinatorics as a main tool, we will see what exactly is happening when the structure approaches its boiling point. Based on joint works with Élie de
Panafieu and Vlady Ravelomanana.
] 22/10/2019
Marie Théret Cardinality of a minimal cutset in first passage percolationabstract.htmlWe consider the model of first passage percolation on Zd in dimension d≥2 : we associate with the edges of the graph a family of i.i.d. non negative random variables. We interpret the random variable associated with an edge as its capacity, i.e., the maximal amount
of water or information that can cross the edge per second. This leads to a natural definition of maximal flow through a bounded domain of the graph from a collection of sources to a collection of sinks. This maximal flow is equal to the minimal capacity of a
cutset, i.e., a set of edges such that if we remove it from the graph we disconnect completely the sources from the sinks. In this talk, we will focus on one of the properties of this minimal cutset : it's cardinality. This is a joint work with Barbara Dembin (LPSM,
Université de Paris).
] 22/10/2019
Robin Stephenson The scaling limit of a critical random directed graphabstract.htmlWe consider the random directed graph G(n,p) with vertex set {1,2,...,n} in which each of the n(n-1) possible directed edges is present independently with probability p . We are interested in the strongly connected components of
this directed graph. A phase transition for the emergence of a giant strongly connected component is known to occur at p = 1/n , with critical window p= 1/n + λ n-4/3 for λ ∈ R . We show that, within this critical
window, the strongly connected components of G(n,p) , rescaled by n-1/3 , converge in distribution to a sequence (C1 ,C2 ,...) of finite strongly connected directed multigraphs with edge lengths which are
either 3-regular or loops. The convergence occurs the sense of an L1 sequence metric for which two directed multigraphs are close if there are compatible isomorphisms between their vertex and edge sets which roughly preserve the edge-lengths. Our
proofs rely on a depth-first exploration of the graph which enables us to relate the strongly connected components to a particular spanning forest of the undirected Erdős-Rényi random graph G(n,p) , whose scaling limit is well understood. We show that the
limiting sequence (C1 ,C2 ,...) contains only finitely many components which are not loops.
] 21/10/2019
Valentin Féray Random permutation factorizationsabstract.htmlWe study random minimal factorizations of the n-cycle into transpositions, which are factorizations of the full cycle (1,...,n) as a product of n-1 transpositions. It is known since Denes (1959) that they are counted by the sequence nn-2 and bijections with Cayley
trees and parking functions have been found. Moreover, these factorizations are naturally encoded (in two different ways) by sequences of non-crossing set of chords of the unit disk.
We establish limit theorems for these sets of chords. The limiting objects are constructed from Levy’s excursion processes and interpolate between the circle and Aldous’ Brownian triangulation. One key step of the proof is to connect our model with conditioned
bitype Galton-Watson trees with offspring distribution varying with $n$, and to find the limit of the contour function of those trees. If time allows, we will also describe the limit of the trajectory of a fixed element in this factorization (in some sense, this is
a local limit result in space).
This is a joint work with Igor Kortchemski.
] 21/10/2019
Jacopo Borga Phase transition for almost square permutationsabstract.htmlA record in a permutation is an entry which is either bigger or smaller than the entries either before or after it (there are four types of records). Entries which are not records are called internal points. We explore scaling limits (called permuton limits) of
uniform permutations in the classes Sq(n,k) of almost square permutations of size n+k with exactly k internal points.
We first investigate the case when k=0, this is the class of square permutations, i.e. permutations where every point is a record. The starting point for our result is a sampling procedure for asymptotically uniform square permutations. Building on that, we
characterize the global behavior by showing that square permutations have a permuton limit which can be described by a random rectangle. We also explore the fluctuations of this random rectangle, which we can describe through coupled Brownian motions.
We then characterize the permuton limit of almost square permutations with k internal points, both when k is fixed and when k tends to infinity along a negligible sequence with respect to the size of the permutation. Here the limit is again a random rectangle but of
a different nature: we will show during the seminar that a phase transition on the shape of the limiting rectangles arises for different values of k.
Joint work with E.Slivken and E. Duchi.
] 21/10/2019
Anne-Laure Basdevant Plus longue sous suite croissante avec contraintesabstract.htmlÉtant donné un nuage de points poissonien, Hammersley étudia dans les années 70 le nombre maximal de points du nuage par lequel un chemin croissant peut passer. Ceci permettait alors d'obtenir la longueur asymptotique de la plus longue sous-suite croissante dans une
grande permutation aléatoire.
Dans cet exposé, nous généraliserons le problème d'Hammersley en rajoutant des contraintes sur le chemin et nous exposerons des couplages qui permettent de se ramener au problème originel.
Travail en collaboration avec Lucas Gerin.
] 21/10/2019
Minmin Wang Prunings, cut trees and the reconstruction problemabstract.htmlWe consider prunings of two families of continuum random trees: the Lévy trees and the inhomogeneous continuum random trees. The so-called cut trees encode the genealogies of the fragmentations that come with the pruning. The reconstruction problem asks how much
information about the initial tree is retained in its cut tree and how to recover it from the cut tree. We propose a new approach to the reconstruction problem, which has been treated previously for the Brownian CRT and for the stable trees. Our approach does not
rely upon self-similarity and can apply to both Lévy trees and inhomogeneous continuum random trees.
Joint work with Nicolas Broutin and Hui He.
] 21/10/2019
Grégory Miermont The breadth-first construction of scaling limits of graphs with finite excessabstract.htmlRandom graphs with finite excess appear naturally in at least two different settings: random graphs in the critical window (aka critical percolation on regular and other classes of graphs),
and unicellular maps of fixed genus. In the first situation, the scaling limit of such random graphs was obtained by Addario-Berry,
Broutin and Goldschmidt based on a depth-first exploration of the graph and on the coding of the resulting forest by random walks. This idea originated in Aldous' work on the critical random graph, using instead a breadth-first search approach that seem less adapted to taking graph scaling limits. We show hat this can be done nevertheless, resulting in some new identities for quantities like the radius and the two-point function of the scaling limit. We also obtain
a similar ``breadth-first'' construction of the scaling limit of unicellular maps of fixed genus. This is based on joint work with Sanchayan Sen.
] 21/10/2019
Christophe Fouqueré Ouverture des Journées MathStic "Probabilités et combinatoire" (21-23 octobre) 15/10/2019
Christian Lavault Sur une erreur fructueuse de Paul Appell (1/4) [abstract.pdf ] 08/10/2019
Michael Engen Permutations containing many patterns [Slides.pdf ]abstract.htmlPermutation patterns is a burgeoning area of combinatorics. While many versions of the question ‘how many patterns can a permutation contain?’
have been asked over the years, each has been viewed in isolation. We present a unified viewpoint for these questions, as well as some answers.
] [article ] 08/10/2019
Gérard Duchamp Domains and a (new ?) family of entire functions 01/10/2019
Mamadou Moustapha Kanté Algorithms listing combinatorial objects from graph theoryabstract.htmlPour une famille d'objets combinatoires $C$ (donnée souvent sous forme d'un oracle),
le problème de génération consiste à lister tous les objets de $C$ sans duplicats.
Cela peut être lister tous les graphes series-parallèles de taille $n$ donnée, ou encore,
lister tous les ensembles satisfaisant une certaine propriété (par exemple les stables d'un graphe donné).
On souhaite mesurer la complexité en temps de tels algorithmes de génération exhaustive,
mais puisque les objets à lister sont souvent en quantité exponentielle par rapport à la taille de l'oracle,
on est intéressé par des algorithmes de temps polynomial en les tailles cumulatives des entrées et sorties (complexité dite "output-sensitive").
L'exposé portera sur les différentes problématiques associées à ces questions et considérera deux familles de problèmes :
sous-graphes maximaux satisfaisant une propriété et les transversaux minimaux.
] 24/09/2019
Claire Levaillant Généralisation du théorème de Wilson modulo p^3 (2/2)abstract.htmlÉtant donné un nombre premier p, on trouve en particulier des
congruences modulo des puissances de p pour les nombres de Stirling
et les nombres harmoniques généralisés en utilisant des techniques p-adiques.
On généralise aussi indépendamment du mathématicien Z-H Sun
(des nombres premiers) un résultat de Glaisher datant de 1900 sur le théorème
de Wilson modulo p^2 au rang p^3.
] 24/09/2019
Claire Levaillant Généralisation du théorème de Wilson modulo p^3 (1/2)abstract.htmlÉtant donné un nombre premier p, on trouve en particulier des
congruences modulo des puissances de p pour les nombres de Stirling
et les nombres harmoniques généralisés en utilisant des techniques p-adiques.
On généralise aussi indépendamment du mathématicien Z-H Sun
(des nombres premiers) un résultat de Glaisher datant de 1900 sur le théorème
de Wilson modulo p^2 au rang p^3.
] 18/09/2019
Sergey Dovgal Soutenance de thèseabstract.htmlDear Colleagues,
I cordially invite you to my PhD defence which will take place in Université Paris 13 18/09/2019, 14:00 next Wednesday, room B107.
Title: Interdisciplinary image of Analytic Combinatorics
Abstract: This thesis is devoted to the development of tools and the use of methods from Analytic Combinatorics, including exact and asymptotic enumeration, statistical properties of random objects, and random generation. Certain focus is put on the
multidisciplinarity of the domain, which is emphasised by using examples from computational logic, statistical mechanics, biology, mathematical statistics, networks and queueing theory.
Rapporteurs:
M Éric Fusy
M Valeriy Liskovets
M Konstantinos Panagiotou
Jury:
Mme Mireille Bousquet-Mélou
M Éric Fusy
M Andrea Sportiello
Mme Brigitte Vallée
Directeurs de thèse:
M Olivier Bodini
M Vlady Ravelomanana
The defence will take place in the room B107, at 14:00, and will be followed by a traditional pot de soutenance, to which everyone is kindly invited. If you intend to come, please write me an email so that we can add submit your name to the security list.
Kind regards, Sergey Dovgal
] 17/09/2019
Samuele Giraudo Pattern avoidance in trees, operads, and enumeration 17/09/2019
Hoang Ngoc Minh Families of eulerian functions involved in the regularizations of divergent polyzetas. 10/09/2019
Sophie Morier-Genoud q-nombres rationnelsabstract.htmlLes suites de nombres classiques ont souvent des q-analogues intéressants.
Les plus connus sont certainement les q-nombres entiers et les q-coefficients binomiaux qui apparaissent tous deux dans différents domaines de mathématique et physique.
En revanche, la notion de q-nombre rationnel n'existe pas vraiment.
On propose une définition basée sur des propriétés combinatoires des rationnels et des fractions continues.
La définition des q-rationnels étend naturellement celle des q-entiers et aboutit à un quotient de polynômes à coefficients entiers positifs.
On donne une interprétation énumérative des coefficients de ces polynômes en termes de graphes et de représentations de carquois.
On remarque aussi des liens avec les polynômes de Jones, les algèbres amassées, et une possible extension
vers une notion de q-nombre réel. Il s'agit d’un travail en commun avec V.Ovsienko.
] 10/09/2019
Gérard Duchamp Non commutative differential equations: localization, independence and unicity [Slides.pdf ] 09/07/2019
Gérard Duchamp 3 formes (utiles) du théorème d'indépendance linéaire (2/2): restriction et localisation 08/07/2019
Tsinjo Rakotoarimalala Complexité de la recherche de motifs dans un texte aléatoire (soutenance de thèse)abstract.htmlJe présenterai les fruits de mon travail de thèse qui s'intitule "Complexité de la recherche de motifs dans un texte aléatoire".
Le jury sera composé de Frédérique Bassino (directrice de thèse),
Julien Clément,
Thierry Lecroq (rapporteur),
Cyril Nicaud (rapporteur),
Mireille Régnier,
Andrea Sportiello.
Vous êtes également conviés au pot qui suivra en salle A201.
Cordialement, Tsinjo Rakotoarimalala
] 02/07/2019
Amir Hashemi Gröbner bases and compact packings 02/07/2019
Gérard Duchamp 3 formes (utiles) du théorème d'indépendance linéaire (1/2) 01/07/2019
Conférence FPSAC et Computational Logic and Applications 26/06/2019
Amir Hashemi Maisons des maths et vulgarisation scientifique en Iran (mercredis du LIPN avec gâteaux iraniens!) 25/06/2019
Conférence Analysis of Algorithms 25/06/2019
Hoang Ngoc Minh Independence properties of a new family of entire functions (2/2) 18/06/2019
Conférence Permutation Patterns 18/06/2019
Gérard Duchamp Combinatorics of characters and continuation of [Slides.pdf ] 18/06/2019
Hoang Ngoc Minh Independence properties of a new family of entire functions (1/2) : Abstract form of a theorem by M. Deneufchâtel 11/06/2019
Matthieu Piquerez Arbres couvrants et généralisation des polynômes de Symanzik en dimensions supérieures [Slides.pdf ]abstract.htmlLes deux polynômes de Symanzik sont des invariants de graphes utilisés en théorie quantique des champs pour calculer des intégrales de Feynman. Le premier polynôme de Symanzik est le dual du polynôme de Kirchhoff pondéré, qui compte le nombre pondéré d'arbres
couvrants d'un graphe. En 2009, Duval, Klivans et Martin ont généralisé la notion d'arbres et le théorème de Kirchhoff en dimensions supérieures (sur les complexes simpliciaux). Nous pouvons de même généraliser les polynômes de Symanzik. Les deux polynômes partagent
de nombreuses propriétés remarquables, notamment une formule de délétion-contraction et une forme déterminantale. Toutefois, nous verrons que la propriété de stabilité par subdivision, propre aux polynômes de Symanzik, rend ces polynômes peut-être plus intéressants
que leurs duaux.
] [article ] 11/06/2019
Gérard Duchamp Towards a Picard-Vessiot theory of noncommutative differential equations (3/3): applications of the abstract form of a theorem by M. Deneufchâtel 05/06/2019
François Bergeron Alice au pays des frises et des pavages [Slides.pdf ]abstract.htmlLa notion de frise d'entiers a été introduite dans les années 1970 par Conway et Coxeter.
Une telle frise correspond à un nombre fini de bandes horizontales superposées d'entiers positifs (>0),
bornées au-dessus et en dessous par des bandes de 1, avec une condition
locale liant ces entiers. Plus explicitement on demande que ad-bc=1, pour toute configuration locale de a, b, c, et d en forme de « diamant »
(a et d se suivent sur une même ligne, avec b et c respectivement juste au-dessus et en dessous).
Conway et Coxeter ont souligné que cela force un phénomène de répétition cyclique horizontale;
de là le terme de frise. Un autre aspect fascinant est qu'il n'y a qu'un nombre fini de telles frises ayant un nombre fixé de lignes,
et qu'elles sont énumérées par les nombres de Catalan. Après un survol de cette notion et de sujets reliés, nous allons en considérer diverses généralisations.
En particulier, on établira des liens avec la formule de condensation de Dogdson (l'auteur d'Alice au pays des merveilles) pour un calcul récursif de déterminants.
] 04/06/2019
Antonio Jimenez Pastor A Computable Extension for Holonomic Functions: DD-Finite Functions [Slides.pdf ]abstract.htmlD-finite functions is a well known class of functions. They are defined via a linear differential equation with polynomial coefficients and we can find many examples
in elementary functions (exp(x), sin(x)), combinatorial generating functions (all P-recursive sequence have a D-finite generating function) and many other special
functions.
In this talk we will see a natural extension to this class: the DD-finite (and, more generically, Dn-finite) functions. These functions are defined using a linear
differential equation with D-finite coefficients. We will described the structural properties known for this larger class of functions.
] 04/06/2019
Gérard Duchamp Towards a Picard-Vessiot theory of noncommutative differential equations (2/3): variations around a theorem by M. Deneufchâtel 28/05/2019
François Bergeron Théorie des espèces, théorie de Pólya, fonctions symétriques et caractères (2/2) 28/05/2019
François Bergeron Théorie des espèces, théorie de Pólya, fonctions symétriques et caractères (1/2) 21/05/2019
François Bergeron Théorie des espèces de structures et applicationsabstract.htmlLa notion d'espèces de structures combinatoires, introduite il y a presque 40 ans,
fournit un contexte conceptuel naturel pour décrire la nature de « structures combinatoires » sur un ensemble. Non seulement des opérations fondamentales entre espèces de structures
permettent d'élaborer naturellement, et de spécifier de nouvelles espèces en termes d'espèce connues; mais cette approche donne directement les identités combinatoires correspondantes. On obtient ainsi une approche systématique à la résolution de problèmes
classiques d'énumération, autant dans leur version étiquetée que non-étiquetée (alias : théorie de Pólya). Nous allons donner une présentation accessible à cette théorie, avec plusieurs illustrations. Si le temps le permet, nous allons survoler différents domaines
d'applications récents au-delà des aspects plus habituels de combinatoire énumérative (physique théorique, chimie, etc.).
] 14/05/2019
Sanjay Ramassamy Extensions of partial cyclic orders, boustrophedons and polytopesabstract.htmlWhile the enumeration of linear extensions of a given poset is a well-studied question, its cyclic counterpart (enumerating extensions to total cyclic orders of a given partial cyclic order) has been subject to very little investigation. In this talk I will
introduce some classes of partial cyclic orders for which this enumeration problem is tractable. Some cases require the use of a multidimensional version of the classical boustrophedon construction (a.k.a. Seidel-Entringer-Arnold triangle). The integers arising from
these enumerative questions also appear as the normalized volumes of certain polytopes.
This is partly joint work with Arvind Ayyer (Indian Institute of Science) and Matthieu Josuat-Verges (Laboratoire d’Informatique Gaspard Monge / CNRS).
] 07/05/2019
Axel Bacher Algorithmes de rattrapage pour la génération aléatoire de chemins (attention horaire exceptionnel suite à comité de sélection de ~13h à ~15h)abstract.htmlCet exposé concerne la génération aléatoire de familles classiques de chemins (Dyck, Motzkin et Schröder et leurs préfixes). Le point de départ est l'algorithme florentin (Barcucci, Pinzani et Sprugnoli 1994+),
qui utilise une méthode de rejet anticipé pour engendrer les préfixes. Je montrerai comment on peut raffiner cet algorithme en utilisant une fonction de « rattrapage » qui permet de fortement réduire, voire d'éliminer, la probabilité de rejet. Les algorithmes obtenus sont asymptotiquement optimaux en termes d'entropie utilisée et significativement plus rapides que les algorithmes florentins.
] 07/05/2019
Christian Lavault Fonctions entières (6/6) 30/04/2019
Hoang Ngoc Minh Towards a Picard-Vessiot theory for noncommutative differential equations (1/3) 23/04/2019
Yi-Ting Chen Towards the uniform random generation in 1-safe Petri nets [Slides.pdf ]abstract.htmlTrace monoids are basic mathematical models of concurrent systems. The probabilistic framework on trace monoids can be found in Abbes and Mairesse (2015) including the uniqueness of uniform measure and random generation. To adopt more practical dynamic
systems, it is essential to take account of ”state”. Conventionally, we model the ”concurrency” by the traces in a trace monoid and model the ”state” by the words in an automaton. Combining these two features, we consider the traces in an automaton, which is equivalent to the executions in a safe Petri net. Our goal is to prove the uniqueness of the uniform measure for partial actions on a trace monoid in order to generate uniformly the infinite executions of a 1-safe Petri net. In this talk, I will present
some properties and the difficulties that we encounter now.
] 16/04/2019
Enrica Duchi Polyominos convexes, permutominos convexes et permutations carréesabstract.htmlDans cet exposé, on s'intéresse aux liens entre trois familles d'objets comptés par des formules closes
remarquablement similaires entre elles. Si le nombre de polyominos convexes est connu depuis les travaux de Delest et Viennot, les formules closes des permutations carrées et permutominoes convexes ont été découvertes plus récemment et sont moins connues mais tout
aussi jolies. Pour expliciter le lien entre ces différentes classes, nous reverrons différentes méthodes d'énumération.
] 09/04/2019
Christian Lavault Fonctions entières (5/6) : ordres, types, factorisations et autres calculs 09/04/2019
Journée Cartes (MathStic): Guillaume Chapuy , Jérémie Bettinelli , Erik Slivken , Luis Fredes 02/04/2019
Nicolas Curien Critical parking on a random tree... and random planar maps!abstract.html
Imagine a plane tree together with a configuration of particles (cars) at each vertex.
Each car tries to park on its node, and if the latter is occupied, it moves downward towards the root trying to find an empty slot.
This model has been studied recently by Bruner and Panholzer as well as Goldschmidt and Przykicki where is it shown that
parking of all cars obeys a phase transition ruled by the density of cars.
We study the annealed critical model of random plane tree together with a parking configuration of cars.
Surprisingly this object is connected to stable looptre e of parameter 3/2 and to processes encountered in the theory of random planar maps!
The talk is based on ongoing work with Olivier Hénard.
] 26/03/2019
Dan Betea From Gumbel to Tracy--Widom II, via integer partitionsabstract.htmlThere are two natural well-studied measures on integer partitions: Plancherel and uniform. In the scaling limit, their first parts behave differently and on a different scale:
Plancherel shows random matrix-type Tracy-Widom statistics (the Baik-Deift-Johansson
theorem), while uniform shows Gumbel, a maximum of independent Gaussians (the Erdős-Lehner theorem).
In this talk, based on joint work with Jérémie Bouttier, we present the 'finite temperature/cylindric' extension of the Plancherel measure,
coming from counting standard Young tableaux of skew shape and interpolating between Plancherel and uniform.
The edge scaling limit yields the finite temperature Tracy-Widom distribution of Johansson, observed in random matrix models and interpolating between
Tracy-Widom and Gumbel statistics. A time-extension of the result yields the finite temperature/periodic extended Airy process of Le Doussal-Majumdar-Schehr.
] 26/03/2019
Christian Lavault Combinatoire du produit de Weierstraß 19/03/2019
Journées Aléa (18-22 mars)19/03/2019
Christian Ikenmeyer Inequalities between plethysm coefficients and Kronecker coefficients via geometric complexity theoryabstract.htmlResearch on Kronecker coefficients and plethysms gained significant momentum when the topics were connected to geometric complexity theory, an approach towards computational complexity lower bounds via algebraic geometry and representation theory. Both types of coefficients appear independently in R. Stanley's list of "Positivity problems and conjectures in algebraic combinatorics".
This talk is about a result that was obtained with geometric complexity theory as motivation, namely an inequality between rectangular Kronecker coefficients and plethysm coefficients.
The proof interestingly uses insights from algebraic complexity theory. As far as we are aware, algebraic complexity theory has never been used before to prove an inequality between representation theoretic multiplicities.
This is joint work with Greta Panova (Rectangular Kronecker coefficients and plethysms in geometric complexity theory, Adv Math 2017).
] 13/03/2019
Christian Ikenmeyer Cours introductif sur le programme de complexité géométrique de Ketan Mulmuley 12/03/2019
TBC 12/03/2019
Christian Lavault Fonctions entières (4/6) : aspects combinatoires 05/03/2019
Séminaire Combinatoire et interactions à l'IHP (François Bergeron, Mathias Lepoutre) 26/02/2019
Noriyoshi Sukegawa On distance computation of marked point process: Mathematical optimization in nonlinear dynamicsabstract.htmlA marked point process is a series of events generated along
the time which is accompanied with some additional information. Examples
of the marked point processes include trades in foreign exchange
markets, earthquake activities, and times at which a neuron fires an
action potential. Calculating a distance between two time windows of a
given marked point process is the first step to analyze it from the
viewpoint of nonlinear dynamics.
] 26/02/2019
Christian Lavault Fonctions entières (3/6) 19/02/2019
Laurent Ménard Recherche en profondeur dans les graphes aléatoires Erdős-Rényiabstract.htmlDans un graphe d'Erdős-Rényi à $N$ sommets et probabilité de connexion $c/N$,
on démontrera que les arbres couvrants de la composante géante construits par des algorithmes d'exploration basés sur la recherche en profondeur convergent vers une limite déterministe explicite.
Cela exhibe entre autres des chemins simples, éventuellement induits, du graphe de longueur linéaire en $N$.
Si le temps le permet j'évoquerai ensuite le cas des graphes construits par modèle de configuration. Ces résultats sont issus de collaborations avec Gabriel Faraud, Nathanaël Enriquez et Nathan Noiry.
] 19/02/2019
Silvia Goodenough
Action de HW sur les tableaux de Riordan 12/02/2019
Journées de combinatoire de Bordeaux (11-13 février)12/02/2019
Gérard Duchamp Théorie locale des polylogarithmes et fonctions polylerch 29/01/2019
Thé combinatoire et discussions sur des problèmes ouverts, code, etc. 29/01/2019
Christian Lavault Fonctions entières (2/6) 22/01/2019
Simon Tricard Nanoparticules et auto-assemblageabstract.htmlLes nanoparticules sont des objets chimiques dont les trois dimensions sont inférieures à 100 nm. L'exposé présentera dans un premier temps les intérêts que suscitent les nanoparticules en tant que telles et les stratégies pour limiter/contrôler leur croissance à l'échelle nanométrique. La deuxième partie abordera le fait de les assembler, la chimie "supraparticulaire" ou leur auto-assemblage dans l'espace et sur surface.
] 22/01/2019
Gérard Duchamp Characters and combinatorics 15/01/2019
Collectif
Galette de rentrée de l'équipe CALIN, énigmes et problèmes ouverts 15/01/2019
Christian Lavault Fonctions entières (1/6) 08/01/2019
Cathy Swaenepoel Chiffres dans les corps finis [Slides.pdf ]abstract.htmlCécile Dartyge et András Sárközy ont introduit une notion de « chiffres » dans les corps finis.
Nous mesurons de manière quantitative le caractère pseudo-aléatoire de ces chiffres en lien avec les opérations de multiplication
et d'addition au travers de l'étude de suites remarquables.
Nos résultats peuvent être réinterprétés à l'aide la notion de trace qui est fondamentale dans les corps finis.
] 08/01/2019
Gérard Duchamp [2019 CIP Start] Program + talk 18/12/2018
Sandro Franceschi Mouvement brownien réfléchi dans des cônes : distribution stationnaire et algébricité de sa transformée de Laplaceabstract.htmlIn the 1970s, William Tutte developed a clever algebraic approach, based on certain “invariants”, to solve a functional equation that arises in the enumeration of properly colored triangulations. The Laplace transform of the stationary distribution of semimartingale
reflected Brownian motion (SRBM) in wedges satisfies similar equations. To be applicable, the method requires the existence of two functions called invariant and decoupling function, respectively. While all models have invariants, we prove that the existence of a
decoupling function is equivalent to a simple geometric condition on the angles. For the models that have in addition a decoupling function, we obtain integral-free expressions of the Laplace transform in terms of the invariants. As a consequence, we obtain new
derivations of the Laplace transform in several well-known cases, as the skew symmetric SRBM, orthogonal reflections, or the Dieker-Moriarty result characterizing sum-of-exponential densities.
Cet exposé est issu d’un travail en cours en collaboration avec Mireille Bousquet-Mélou, Charlotte Hardouin, Andrew Elvey Price et Kilian Raschel
] 18/12/2018
Collectif Extensions algébriques et analytiques des polylogarithmes 11/12/2018
États de la recherche SMF : mécanique statistique (10-14 déc)11/12/2018
Christian Lavault Transformées et représentations intégrales de fonctions spéciales usuelles en plusieurs variables (2/2) 04/12/2018
Nina Holden Percolation on triangulations: A bijective path to Liouville quantum gravityabstract.htmlWe set the foundation for a series of works aimed at proving strong relations between uniform random planar maps and Liouville quantum gravity (LQG). Our method relies on a bijective encoding of site-percolated planar triangulations by certain 2D lattice paths. Our
bijection parallels in the discrete setting the mating-of-trees framework of LQG and Schramm-Loewner evolutions (SLE) introduced by Duplantier, Miller, and Sheffield. Combining these two correspondences allows us to relate uniform site-percolated
triangulations to $\sqrt{8/3}$-LQG and SLE${}_6$. In particular, we establish the convergence of several functionals of the percolation model to continuous random objects defined in terms of $\sqrt{8/3}$-LQG and SLE${}_6$. For instance, we show that the exploration tree of the
percolation converges to a branching SLE${}_6$, and that the collection of percolation cycles converges to the conformal loop ensemble CLE${}_6$. We also prove convergence of counting measure on the pivotal points of the percolation. Our results play an essential role in
several other works, including a program for showing convergence of the conformal structure of uniform triangulations and works which study the behavior of random walk on the uniform infinite planar triangulation.
(Joint work with Olivier Bernardi and Xin Sun.)
] [article ] 04/12/2018
Christian Lavault Transformées et représentations intégrales de fonctions spéciales usuelles en plusieurs variables (1/2) 29/11/2018
Séminaire Flajolet Mireille Bousquet-Mélou, Charles Bordenave, Vincent Delacroix 28/11/2018
Nicolas Broutin La combinatoire du problèmes des balles (exposé au LAGA, suivi d'un exposé d'Elie Aïdékon sur le mouvement brownien plan) 27/11/2018
Wenjie Fang Hypergraphes aléatoires sous-critiques, composantes d'ordre supérieur et hyperarbresabstract.htmlDans le modèle de graphe aléatoire d'Erdős–Rényi $G(n,p)$,
l'émergence de la composante géante se situe à la fenêtre $p=n^{-1}+O(n^{-4/3})$. Lorsque $p$ varie de $(1-\epsilon)n^{-1}$ (sous-critique) à $n^{-1}$, puis à $(1+\epsilon)n^{-1}$,
la plus grande composante varie de $O(\epsilon^{-2}\log(n\epsilon^3))$ à $\Theta(n^{2/3})$, puis $(1+o(1)) 2 \epsilon n$. Nous considérons une généralisation de $G(n,p)$ sur les hypergraphes k-uniformes, avec une notion de connexité d'ordre supérieur. Plus précisément, pour $1 \leq j < k$, considérons les ensembles de j sommets, appelés les j-ensembles. Deux j-ensembles sont j-connexes s'il existe entre eux un chemin d'hyperarêtes dont l'intersection de deux hyperarêtes consécutives contient au moins $j$ sommets. Une composante j-connexe est une famille maximale de j-ensembles qui sont j-connexes l'un à l'autre. Sous cette notion de j-connexité, nous avons déterminé, dans un régime sous-critique, la taille précise des $m$ plus grandes composantes j-connexes, et aussi leur structure. C'est un travail joint avec Oliver Cooley, Nicola Del Giudice et Mihyun Kang.
] 22/11/2018
Journée de la recherche inter-labos de l'institut Galilée 20/11/2018
Hoang Ngoc Minh Majoration des coefficients de Chen par la méthode du cercle 06/11/2018
Olivier Bodini Discussion autour des bounding chains pour les chaînes de Markov pour sampler des pavages de type "hard ball" 06/11/2018
Gérard Duchamp Algebraic independence of characters followed by About the deformation of polylogarithms 30/10/2018
Hoang Ngoc Minh A family of Eulerian functions involved in regularization of divergent polyzetas (3/3) 23/10/2018
Erik Slivken Large random pattern-avoiding permutationsabstract.htmlA pattern in a permutation is a subsequence with a specific relative order. What can we say about a typical large random permutation that avoids a particular pattern? We use a variety of approaches. For certain classes we give a geometric description that relates
these classes to other types of well-studied random objects like random walks or random trees. Using the right geometric description we can find the the distribution of certain statistics like the number and location of fixed points. Earlier work dealt with
permutations that avoid a pattern of length 3 using a variety of bijections. More recently, using connections with random walks in cones, we show certain scaling limits for permutations avoiding longer monotone patterns are given by traceless Dyson Brownian
motion. This is joint work with Christopher Hoffman and Douglas Rizzolo.
] 23/10/2018
Gérard Duchamp Program + Unanswered questions 16/10/2018
François Bergeron Généralisations de la conjecture de Foulkesabstract.htmlEn 1950, Foulkes a formulé une conjecture simple sur le pléthysme de fonction symétriques qui n’est toujours pas résolue aujourd’hui. De fait, elle avait déjà été énoncée (sous une autre forme) par Hadamard en 1897. Assez récemment, elle a été généralisée d’une façon qui soulève plusieurs jolis problèmes de combinatoire énumérative, que nous allons décrire.
Puis, après avoir mis en place les concepts nécessaires et discuté des avancées sur la question, nous allons présenter de nouvelles conjectures encore plus générales (incluant des $q$-analogues), et montrer quelques résultats associés.
] 16/10/2018
Gérard Duchamp Combinatorics of characters, Schützenberger's calculus and indexing continuation of polylogarithms 09/10/2018
Hoang Ngoc Minh A family of Eulerian functions involved in regularization of divergent polyzetas (2/3) 02/10/2018
Thomas Fernique Sur les 164 façons d'empiler trois cercles 02/10/2018
Hoang Ngoc Minh A family of Eulerian functions involved in regularization of divergent polyzetas (1/3) 02/10/2018
Gérard Duchamp Stars of the plane and their composition 25/09/2018
Journées MathStic
Journées de Géométrie et Combinatoire dans les Espaces des Modules (24-25 septembre): Corentin Boissy, Vincent Delecroix, Quentin De Mourgues, Giovanni Forni, Vaibhav Gadre, Elise Goujard, Rodolfo Gutierrez, Carlos Matheus20/09/2018
Séminaire Flajolet Arnaud de Mesmay, Frédéric Jouhet, Bénédicte Haas 18/09/2018
Rado Rakotonarivo Une chaîne de Markov pour les polytopes entiersabstract.htmlNous présenterons une approche pour faire de la génération aléatoire de polytopes entiers en utilisant les chaînes de Markov. Les objets à engendrer sont les polytopes entiers contenus dans l'hypercube ${[0,k]}^d$, notés $(d,k)$-polytopes. On s’intéresse à la
distribution uniforme sur nos objets. La construction du générateur aléatoire se fait de la manière suivante : modéliser une chaîne de Markov dont les états seront les $(d,k)$-polytopes, lancer des marches sur la chaîne jusqu'à ce qu'on soit assez proche d'une
distribution stationnaire. Notre principal résultat est que cette distribution stationnaire est unique et uniforme. Je présenterai également des résultats sur le temps de mélange de notre chaîne.
] 11/09/2018
Martin Milanič Decomposing 1-Sperner hypergraphs, with applications to graphsabstract.htmlA hypergraph is Sperner if no hyperedge contains another one. A Sperner hypergraph is equilizable (resp., threshold) if the characteristic vectors of its hyperedges are the (minimal) binary solutions to a linear equation (resp., inequality) with positive
coefficients. These combinatorial notions have many applications and are motivated by the theory of Boolean functions and integer programming. We introduce the class of 1-Sperner hypergraphs, defined by the property that for every two hyperedges the smallest of
their two set differences is of size one. We characterize this class of Sperner hypergraphs by a decomposition theorem and derive several consequences from it, including bounds on the size of 1-Sperner hypergraphs, a proof that every 1-Sperner hypergraph is both
threshold and equilizable, and an efficient algorithm for genera ting the minimal transversals within this class of hypergraphs. Several applications of 1-Sperner hypergraphs and their structure to graphs will also be discussed, including new characterizations of
threshold graphs and new classes of graphs of bounded clique-width.
The talk is based on joint works with Endre Boros and Vladimir Gurvich.
] [article ] [article ] 11/09/2018
60th Birthday of Christian Krattenthaler Strobl, September 9 - 12 2018 10/07/2018
Gérard Duchamp Élimination de relateurs dans \(DK_n\) et codage de la factorisation Mélançon-Reutenauer-Schützenberger 03/07/2018
Justine Falque Algèbre des orbites des groupes à profil polynomial, preuve des conjectures de Cameron et de Macphersonabstract.htmlÉtant donné un groupe de permutation infini G, on définit la fonction qui à tout
entier naturel n associe le nombre d'orbites de sous-ensembles de cardinal n,
pour l'action induite de G sur les sous-ensembles d'éléments.
Cameron a conjecturé que cette fonction de comptage (le profil de G) est un
quasi-polynôme dans le cas où sa croissance est polynomiale.
Une autre conjecture, plus forte, a été émise plus tard par un de ses étudiants,
Macpherson. Elle concerne une certaine structure d'algèbre graduée sur les orbites
de sous-ensembles, créée par Cameron, et suppose que si le profil de G est
polynomial, alors son algèbre des orbites est de type fini.
L'exposé présentera ces deux conjectures et leur contexte, ainsi que les idées de
la preuve de la conjecture de Macpherson, fruit d'un travail commun avec Nicolas
Thiéry (avec les conseils précieux de Peter Cameron lui-même).
] 03/07/2018
Pablo Rotondo Efficient GCD computation: the continued logarithm algorithm and ergodic theoryabstract.htmlIntroduced by Gosper in 1978, the Continued Logarithm Algorithm computes the gcd of two integers efficiently, performing only shifts and subtractions. Shallit has studied its worst-case complexity in 2016, showing it to be linear. Here, we perform the average-case analysis of the algorithm: we study its main parameters (number of iterations, total number of shifts) and obtain precise asymptotics for their mean values, with explicit constants. Our analysis involves the dynamical system underlying the algorithm, which produces continued fraction expansions whose quotients are powers of 2. Even though studied by Chan in 2005, this system from an Ergodic Theory perspective, the presence of powers of 2 in the quotients gives a dyadic flavour which cannot be analysed only with Chan's results. Thus we introduce a dyadic component and deal with a two-component dynamical system. With this new mixed system at hand, we provide a complete average-case analysis of the algorithm.
] 03/07/2018
Paulina Cecchi Dendric words and dendric subshifts [Slides.pdf ]abstract.htmlTo every factor w of an infinite word x in a finite alphabet,
we can associate a bipartite graph, called the extension graph of w, in
which one puts edges between left and right copies of letters a, b such
that awb is a factor of x. The word x is said to be dendric if for all
factor w of x, the extension graph of w is a tree. Dendric words are
therefore defined in terms of combinatorial properties of their language.
Dendric subshifts are symbolic systems defined using dendric words. We
will talk about some dynamical properties of dendric subshifts.
] 03/07/2018
Delphin Sénizergues Degrés limites dans les arbres à attachement préférentiel affineabstract.html On introduit le modèle d'arbres suivant. On se donne une suite arbitraire de nombres réels positifs $(a_n)_{n\geq 1}$. On définit $T_1$ comme l'arbre à un seul sommet d'étiquette $1$. Si $T_n$ est déjà construit, $T_{n+1}$ est obtenu en rajoutant un sommet étiqueté
$n+1$ à l'arbre $T_n$. Le nouveau sommet est un enfant du sommet $k\geq n$ avec une probabilité proportionnelle à $a_k+deg(k)$, où $deg(k)$ est le degré du sommet dans l'arbre $T_n$.
On s'intéressera à l'évolution de la suite des degrés des sommets de l'arbre. Sous certaines conditions sur la suite des réels $(a_n)_{n\geq 1}$, la suite des degrés adéquatement renormalisés converge p.s. (dans $l^p$ pour p assez grand) vers une suite aléatoire,
qui peut être décrite comme les accroissements successifs d'une chaîne de Markov. Pour certaines suites $(a_n)$, la loi de la chaîne de Markov est même explicite. La preuve utilise des résultats classiques sur les urnes de Pólya, que je rappellerai.
] [article ] 26/06/2018
Florian Girelli Combinatorial physics 19/06/2018
Christophe Tollu Théorie géométrique de la complexité (4/4)abstract.htmlLa théorie géométrique de la complexité (GCT) est un programme de recherche lancé par K. Mulmuley et M. Sohoni aux alentours de 2000 pour attaquer la variante algébrique, due à L. Valiant, de la conjecture centrale de la théorie de la complexité, l'hypothèse de Cook
$P \neq NP$. Ce programme substitue aux hypothèses de Cook et de Valiant une conjecture de nature géométrique, à laquelle les formidables outils de la géométrie algébrique et de la théorie des représentations peuvent être appliqués. Dans l'esprit de ses promoteurs,
la GCT avait aussi pour but de permettre de démontrer l'existence de minorants de complexité ("lower bounds" en franglais) par la production effective de témoins. Dans ce mini-tutoriel sur la GCT, je présenterai le programme initial de Mulmuley-Sohoni, quelques-uns
des développements récents et des obstacles qui sont apparus dans sa réalisation.
Aucune compétence particulière en géométrie ou en théorie des représentations n'est requise des participants.
] 19/06/2018
Christophe Tollu Théorie géométrique de la complexité (3/4)abstract.htmlLa théorie géométrique de la complexité (GCT) est un programme de recherche lancé par K. Mulmuley et M. Sohoni aux alentours de 2000 pour attaquer la variante algébrique, due à L. Valiant, de la conjecture centrale de la théorie de la complexité, l'hypothèse de Cook
$P \neq NP$. Ce programme substitue aux hypothèses de Cook et de Valiant une conjecture de nature géométrique, à laquelle les formidables outils de la géométrie algébrique et de la théorie des représentations peuvent être appliqués. Dans l'esprit de ses promoteurs,
la GCT avait aussi pour but de permettre de démontrer l'existence de minorants de complexité ("lower bounds" en franglais) par la production effective de témoins. Dans ce mini-tutoriel sur la GCT, je présenterai le programme initial de Mulmuley-Sohoni, quelques-uns
des développements récents et des obstacles qui sont apparus dans sa réalisation.
Aucune compétence particulière en géométrie ou en théorie des représentations n'est requise des participants.
] 12/06/2018
Christophe Tollu Théorie géométrique de la complexité (2/4)abstract.htmlLa théorie géométrique de la complexité (GCT) est un programme de recherche lancé par K. Mulmuley et M. Sohoni aux alentours de 2000 pour attaquer la variante algébrique, due à L. Valiant, de la conjecture centrale de la théorie de la complexité, l'hypothèse de Cook
$P \neq NP$. Ce programme substitue aux hypothèses de Cook et de Valiant une conjecture de nature géométrique, à laquelle les formidables outils de la géométrie algébrique et de la théorie des représentations peuvent être appliqués. Dans l'esprit de ses promoteurs,
la GCT avait aussi pour but de permettre de démontrer l'existence de minorants de complexité ("lower bounds" en franglais) par la production effective de témoins. Dans ce mini-tutoriel sur la GCT, je présenterai le programme initial de Mulmuley-Sohoni, quelques-uns
des développements récents et des obstacles qui sont apparus dans sa réalisation.
Aucune compétence particulière en géométrie ou en théorie des représentations n'est requise des participants.
] 12/06/2018
Christophe Tollu Théorie géométrique de la complexité (1/4)abstract.htmlLa théorie géométrique de la complexité (GCT) est un programme de recherche lancé par K. Mulmuley et M. Sohoni aux alentours de 2000 pour attaquer la variante algébrique, due à L. Valiant, de la conjecture centrale de la théorie de la complexité, l'hypothèse de Cook
$P \neq NP$. Ce programme substitue aux hypothèses de Cook et de Valiant une conjecture de nature géométrique, à laquelle les formidables outils de la géométrie algébrique et de la théorie des représentations peuvent être appliqués. Dans l'esprit de ses promoteurs,
la GCT avait aussi pour but de permettre de démontrer l'existence de minorants de complexité ("lower bounds" en franglais) par la production effective de témoins. Dans ce mini-tutoriel sur la GCT, je présenterai le programme initial de Mulmuley-Sohoni, quelques-uns
des développements récents et des obstacles qui sont apparus dans sa réalisation.
Aucune compétence particulière en géométrie ou en théorie des représentations n'est requise des participants.
] 07/06/2018
Séminaire Flajolet Matjaz Konvalinka , Vlady Ravelomanana 05/06/2018
Jesper Lykke Jacobsen Entropie au bord universelle dans la percolation bidimensionnelleabstract.htmlNous calculons l'entropie au bord pour la percolation d’arêtes sur le réseau carré, dans la présence d’un poids statistique pour les boucles qui touchent le bord. Ainsi, nous obtenons des expressions exactes pour le ruban et le cylindre de taille L. Pour le
cylindre, nous présentons une analyse asymptotique rigoureuse qui permet le calcul des corrections de taille finie à un ordre arbitraire. Pour le ruban, nous donnons des expressions exactes qui ont été vérifiées par des calculs numériques de haute précision. Nos
résultats rigoureux viennent en appui à un argument basé sur la théorie conforme des champs, en particulier en ce qui concerne les corrections logarithmiques universelles pour le cas du ruban, dues aux effets géométriques des coins.
] 05/06/2018
Christophe Tollu Théorie de la complexité et géométrie des orbites du déterminant et du permanentabstract.htmlAprès un rappel sur les circuits arithmétiques et le problème de Valiant (VP vs VNP), je présenterai quelques résultats récents sur la "complexité déterminantale" du permanent, puis montrerai comment la version purement algébrique du problème VP vs VNP se prête à une reformulation en termes de géométrie des orbites du déterminant et du permanent (pour l'action d'un groupe algébrique sur les polynômes homogènes). Plusieurs ingrédients de base du programme de théorie géométrique de la complexité de Mulmuley et Sohoni seront présentés au cours de l'exposé bien que celui-ci ne soit pas "A crash course on Geometric Complexity Theory
] 29/05/2018
Nicolas Behr Combinatorics of chemical reactionsabstract.htmlReporting on recent work with G.H.E. Duchamp and K.A. Penson (arXiv:1712.06575), I plan to present a formulation of chemical reaction systems in the so-called stochastic mechanics formalism. This approach allows to uncover some deep relationships between the combinatorial techniques of boson normal-ordering and the dynamics of chemical reaction networks: each semi-linear reaction type induces an evolution within a space of probability distributions that can be computed explicitly via our techniques. For the interesting remaining types of reactions, some results involving systems of Sobolev-Jacobi orthogonal polynomials will be presented.
] 23/05/2018
Roberto Baldacci A new branch-and-price-and-cut algorithm for one-dimensional bin packing problemsabstract.htmlIn this work, a new branch-and-price-and-cut algorithm is proposed to solve the one-dimensional bin packing problem (1D-BPP). The 1D-BPP is one of the most fundamental problems in combinatorial optimization and has been extensively studied for decades. Recently,
Delorme et al. (2016) proposed 500 new test instances for the 1D-BPP; the best exact algorithm proposed in the literature can optimally solve 167 of these new instances, with a time limit of one hour imposed to each execution of the algorithm. The exact algorithm
proposed in this paper is based on the classical set-partitioning model for the 1D-BPP and the subset-row inequalities proposed by Jepsen et al. (2008). We describe an ad-hoc label-setting algorithm to solve the pricing problem, dominance and fathoming rules to
speedup its computation and a new primal heuristic. The exact algorithm can easily handle some practical constraints, like the incompatibility between the items, and therefore we also apply it to solve the 1D-BPP with conflicts (1D-BPPC). The proposed method is
tested on a large family of 1D-BPP and 1D-BPPC classes of instances. For the 1D-BPP, the proposed method can optimally solve 237 instances of the new set of difficult instances; the largest instance involves 1003 items and bins of capacity 80,000. For the 1D-BPPC,
the experiments show that the method is highly competitive with state-of-the-art methods, and successfully closed several open 1D-BPPC instances.
] 23/05/2018
Florian Luca Facteurs premiers de nombres remarquables (exposé grand public aux mercredis du LIPN)abstract.htmlSoit \(a_n\) une suite de nombres entiers et considérons le produit \(\prod_{n=1}^{N} a_n\).
Combien ce produit a-t-il de facteurs premiers ? Quel est le plus grand ?
Nous présenterons différents résultats concernant des suites célèbres : les nombres de Fermat, de Fibonacci, \(n!+1\)...
] 22/05/2018
Guillaume Chapuy Énumération de variétés triangulées en dimension d≥3 abstract.htmlEn dimension d≥3, on prend n simplexes, et on recolle leurs facettes de manière arbitraire. On obtient ainsi un espace topologique qui est a priori une pseudo-variété, mais pas toujours une variété. De combien de manière peut-on le faire, asymptotiquement, pour
obtenir une variété? On donne des réponses (très) partielles à cette question sous la forme de bornes inférieures et supérieures superexponentielles. En particulier on détermine le comportement surexponentiel en dimension 3, dans le cas des triangulations coloriées
issues des modèles de tenseur. Au passage on croise des questions rigolotes et nouvelles d'énumération de graphes que nous laissons partiellement ouvertes. Travail en commun avec Guillem Perarnau.
] 22/05/2018
Anna Ben Hamou Temps de mélange de marches aléatoires sur des graphes aléatoiresabstract.htmlDans cet exposé, nous commencerons par rappeler la notion de temps de mélange d'une chaîne de Markov et introduirons le phénomène de cutoff, qui décrit une convergence très abrupte à l'équilibre. Établir le cutoff pour une chaîne donnée requiert souvent une analyse
extrêmement fine, et il existe assez peu de résultats généraux permettant par exemple d'exhiber des grandes classes de graphes sur lesquels la marche aléatoire présente le cutoff. On peut alors se demander ce qu'il se passe sur un graphe « typique ». Nous
considérerons le cas des graphes aléatoires à suite prescrite de degrés, et montrerons qu'avec forte probabilité, sur de tels graphes, la marche aléatoire simple et la marche aléatoire dite « sans rebroussement » présentent le cutoff. En interprétant les temps de
mélange comme des entropies limites sur un arbre de Galton-Watson qui constitue une approximation locale du graphe, nous montrerons de plus que la marche aléatoire sans rebroussement mélange plus vite que la marche simple. Ces résultats sont issus de collaborations
avec Justin Salez (Paris Diderot), Eyal Lubetzky (NYU) et Yuval Peres (Microsoft Research).
] 22/05/2018
Alain Rouault Troncatures de matrices de Haar et draps browniens [Slides.pdf ]abstract.htmlCe travail (en collaboration avec C. Donati-Martin et V. Beffara) est une extension d'un article de G. Chapuy (2007), obtenue en remplaçant le groupe des permutations d'ordre n muni de la probabilité uniforme par le groupe unitaire (resp. orthogonal) d'ordre n. On
définit ainsi une suite indexée par n de processus à deux paramètres qui converge en loi vers un drap brownien. Les preuves mettent en jeu la combinatoire associée au calcul de Weingarten.
] 22/05/2018
Michael Wallner Periodic Pólya urns and an application to Young tableauxabstract.htmlPólya urns are urns where at each unit of time a ball is drawn uniformly at random and is replaced by some other balls according to its colour.
We introduce a more general model: The replacement rule depends on the colour of the drawn ball and the value of the time mod p.
Our key tool are generating functions, which encode all possible urn compositions after a certain number of steps.
The evolution of the urn is then translated into a system of differential equations and we prove that the moment generating functions are D-finite.
From these we derive asymptotic forms of the moments.
When the time goes to infinity, we show that these periodic Pólya urns follow a rich variety of behaviours:
their asymptotic fluctuations are described by a family of distributions, the generalized Gamma distributions, which can also be seen as powers of Gamma distributions.
Furthermore, we establish some enumerative links with other combinatorial objects, and we give an application for a new result on the asymptotics of Young tableaux:
This approach allows us to prove that the law of the lower right corner in a triangular Young tableau follows asymptotically a product of generalized Gamma distributions.
] 22/05/2018
Journée MathStic
Combinatoire, probabilités, et physique 15/05/2018
CALIN
Réunion d'équipe 15/05/2018
Mario Valencia-Pabon Hom-idempotent graphs, normal Cayley graphs and stable Kneser graphsabstract.htmlDans cet exposé, on parlera de la notion de hom-idempotence dans l'ensemble de graphes : un graphe $G$ est dit hom-idempotent s'il existe un homomorphisme entre le graphe produit cartésien $G*G$ et $G$ lui-même. Cette notion est fortement liée à une classe
particulière de graphes de Cayley qu'on appelle les graphes de Cayley normaux. On montrera que les graphes de Kneser $K(n,k)$ ne sont pas hom-idempotents. On montrera aussi que les graphes s-stables de Kneser $K(n,k)_s$ ne sont pas hom-idempotents si $s=2$ mais,
pour $n=sk+1$, $K(n,k)_s$ est hom-idempotent. Finalement, on appliquera la notion de hom-idempotence à la $k$-tuple coloration de graphes : une $k$-tuple coloration de graphes consiste en affecter à chaque sommet un $k$-ensemble de couleurs de sorte que sommets
adjacents reçoivent $k$-ensembles disjoints. On montrera que la différence entre le nombre chromatique du graphe produit cartésien de graphes de Kneser $K(n,k)*K(n,k)$ et le nombre chromatique d'une 2-tuple coloration du même graphe $K(n,k)*K(n,k)$ n'est pas bornée.
] 15/05/2018
Mehdi Naima Phylogenetic trees modeled by increasing Schröder treesabstract.htmlIn biology a phylogenetic tree is a classical tool to represent the evolutionary relationship among
species. Our main frustration against the classical combinatorial models is related to the chrono-
logical aspect that seems not considered by the models. E. g. the Schröder trees do not take into
account the time evolution. We develop in this paper a model for phylogenetic trees satisfying
in priority two constraints: (1) to take into account the chronological evolution and (2) to be
efficient to simulate. Our model is based on some increasingly labeling of Schröder trees.
] 02/05/2018
Gleb Koshevoy Discrete convexity and applications to combinatorics and optimizationabstract.htmlI will explain theory convexity for lattices, free Abelian groups without torsion. I will show that a famous class of polytopes, polymatroids of combinatorial optimization, is related to one of classes of discrete convexity. Several instances of discretely convex
functions related to combinatorics of Young tableaux will be demonstrated.
] 24/04/2018
Florian Luca Facteurs cyclotomiques des polynômes de Serreabstract.htmlOn considère la famille des polynômes \(P_m(X)\in {\mathbb Q}[X]\) donnée par
$$\prod_{m\ge 1} (1-q^m)^{-z}=\sum_{m\ge 0} P_m(z) q^m.$$
Ces polynômes ont des connexions profondes avec la théorie des nombres (pour les partitions d'entiers) et avec la fonction \(\tau\) de Ramanujan. Ils sont apparus pour la première fois dans le travail
de Newman de 1955, et ont été utilisé par Serre dans son travail de 1985 sur la lacunarité des puissances de la fonction \(\eta\) de Dedeking. Ils peuvent être
donnés aussi par \(P_0(X)=1\) et
$$P_m(X)=\frac{X}{m}\left(\sum_{k=1}^m \sigma(k) P_{m-k}(X)\right)\qquad {\text{ pour}}\qquad m\ge 1.$$
Il est facile de voir que \(P_m(X)\) n'a aucune racine positive. De plus, par la formule pentagonale d'Euler,
on déduit que \(X+1\mid P_m(X)\) pour un nombre infini de \(m\). On se pose la question de savoir
si \(P_m(X)\) peut avoir comme zéro d'autres racines de l'unité différentes de \(-1\). On montre que cela n'est jamais le cas, c'est-à-dire que si \(\zeta\) est une racine d'unité d'ordre \(N\ge 3\) et \(m\ge 1\), alors \(P_m(\zeta)\ne 0\). La preuve utilise des resultats classiques sur les corps finis, et un petit peu de théorie analytique des nombres.
] 24/04/2018
Hoang Ngoc Minh Théorie de Picard-Vessiot et équations différentielles non commutatives 17/04/2018
Christelle Rovetta Utilisation de la programmation dynamique comme stratégie pour l'algorithme de simulation parfaite [Slides.pdf ]abstract.htmlEn 1996, Propp et Wilson ont proposé un algorithme permettant l'échantillonnage sans biais de la distribution stationnaire d'une chaîne de Markov ergodique. Ce dernier appelé aussi algorithme de simulation parfaite, requiert la simulation en parallèle de tous les états possibles de la chaîne. Un des challenges lorsque l'on veut faire de l'échantillonnage par simulation parfaite réside généralement à mettre en place des stratégies permettant de ne pas avoir à simuler toutes les trajectoires.
Un réseau fermé de files d'attente est un réseau dans lequel les clients ne peuvent ni entrer ni quitter le réseau. La dynamique de tels réseaux est couramment représentée par une chaîne de Markov ergodique. La difficulté pour qui voudrait appliquer l'algorithme de Propp et Wilson à de tels réseaux, réside dans la taille de l'espace des états qui est exponentielle en le nombre de files à laquelle s'ajoute une contrainte globale à savoir le nombre constant de clients.
] 12/04/2018
Séminaire Flajolet Cesar Ceballos, Hugo Duminil-Copin, Bérénice Delcroix-Oger 10/04/2018
Gérard Duchamp Eq. diff. non commutatives (préparation)abstract.htmlLes structures dans lesquelles l'ordre des opérateurs est important se codent facilement par des mots. Il en est ainsi des intégrales itérées. Nous montrerons qu'alors, considérer la serie génératrice (non-commutative) permet de se ramener à une équation différentielle (non-commutative) très simple pour laquelle on peut développer un "calculus" élémentaire et très puissant.
] 03/04/2018
Journées du GDR-IM (du 3 au 6 avril, le 6 est une journée en hommage à Maurice Nivat) 27/03/2018
Gleb Koshevoy Cluster relations among Schur functions and a positivity conjectureabstract.htmlCluster algebras, invented by Sergey Fomin and Andrei Zelevinsky around 2000,
are commutative algebras whose generators and relations are constructed in a recursive manner.
Due to cluster recursion we obtain Laurent polynomials in the initial variables, so-called Laurent
phenomenon of cluster algebras. The coordinate ring of base affine space C[N_-\SL_n] plays an important role
in representation theory and is endowed with a cluster algebra structure. We show that under specialization of minors to
Schur functions, Laurent polynomials of this cluster algebra turn into 'homogeneous' sums of Schur function. A positivity conjecture says that these sums have positive coefficients. This conjecture is true for finite cluster subalgebras.
] 27/03/2018
Gleb Koshevoy Combinatorial bases of KZn (discussion) 21/03/2018
Christina Goldschmidt Parking on a treeabstract.htmlConsider the following particle system. We are given a uniform
random rooted tree on vertices labelled by {1,2,...,n }, with
edges directed towards the root. Each node of the tree has space for a
single particle (we think of them as cars). A number m of cars
arrives one by one, and car i wishes to park at node Si , where S1 , S2 ,... , Sm are i.i.d. uniform random variables on
{1,2,...,n }. If a car arrives at a space which is already occupied, it follows
the unique path oriented towards the root until the first time it encounters
an empty space, in which case it parks there; otherwise, it leaves the
tree. Let An,m denote the event that all m cars find spaces in the
tree. Lackner and Panholzer proved (via analytic combinatorics methods)
that there is a phase transition in this model. Set m = [α n ].
Then if α ≤ 1/2, P (An,[α n] ) →
sqrt(1-2α )/(1-α ), whereas if α > 1/2 we have
P (An,[α n] ) → 0 . (In fact, they proved more precise asymptotics
in n for α ≥ 1/2.) In this talk, I will give a probabilistic
explanation for this phenomenon, and an alternative proof via the objective
method. Time permitting, I will also discuss some generalisations.
] 20/03/2018
Antoine Deza On lattice polytopes, convex matroid optimization, and degree sequences of hypergraphs [Slides.pdf ]abstract.htmlWe introduce a family of polytopes, called primitive zonotopes, which can be seen as a generalization of the permutahedron of type Bd . We discuss connections to the largest diameter of lattice polytopes and to the computational complexity of multicriteria matroid
optimization. Complexity results and open questions are also presented. In particular, we answer a question raised in 1986 by Colbourn, Kocay, and Stinson by showing that deciding whether a given sequence is the degree sequence of a 3-hypergraph is computationally
prohibitive. Based on joint works with Asaf Levin (Technion), George Manoussakis (Paris Sud), Shmuel Onn (Technion).
] 20/03/2018
Sergey Dovgal Pólya enumeration theorem from scratch (3/3) + présentation de projetsabstract.htmlI am going to talk about very popular combinatorial connection between ordinary and exponential generating functions which is
called cycle index function. I am going to define the combinatorial species according to the book "Theory of Species"
by Bergeron, Labelle, Leroux, and present their beautiful proof of the cycle index composition theorem.
The proof relies on the theory of symmetric functions in infinitely many variables.
This proof is a beautiful example of Grothendieck's concept: in order to prove something particular,
one should make a more general statement and prove it.
] 13/03/2018
Journées Aléa 2018 (12-16 mars 2018)06/03/2018
Sidi-Mohamed Sedjelmaci Two fast parallel GCD algorithms of many integers [Slides.pdf ]abstract.htmlOn montre que le calcul du PGCD de 𝑚 integers de 𝑂(𝑛) bits
peut se faire en parallèle en temps
𝑂(𝑛 / log 𝑛) avec 𝑂(𝑚𝑛1+𝜖 ) processors, pour tout
2 ≤ 𝑚 ≤ 𝑛3/2 / log 𝑛, c'est-à-dire que le temps de calcul en parallèle
ne dépend pas dépend du nombre d'entiers m considéré dans cet intervalle.
] 06/03/2018
Sergey Dovgal Pólya enumeration theorem from scratch (2/3) + discussionabstract.htmlI am going to talk about very popular combinatorial connection between ordinary and exponential generating functions which is
called cycle index function. I am going to define the combinatorial species according to the book "Theory of Species"
by Bergeron, Labelle, Leroux, and present their beautiful proof of the cycle index composition theorem.
The proof relies on the theory of symmetric functions in infinitely many variables.
This proof is a beautiful example of Grothendieck's concept: in order to prove something particular,
one should make a more general statement and prove it.
] 28/02/2018
STACS , à Caen (28 février-3 mars)20/02/2018
Jérémie Bettinelli Disques browniens [Slides.pdf ]abstract.htmlÀ l'instar du mouvement brownien qui apparaît comme limite d'échelle universelle de toute marche aléatoire raisonable, les disques browniens sont des espace métrique aléatoires qui apparaissent comme limite d'échelle universelle de modèles raisonables de cartes
aléatoire du disque. Ces objets généralisent la carte brownienne de Miermont et Le Gall obtenue en considérent des cartes aléatoire de la sphère.
Nous présenterons les disques browniens et en donneront quelques propriétés remarquables. Ce travail est en commun avec Grégory Miermont.
] 20/02/2018
Sergey Dovgal Pólya enumeration theorem from scratch (1/3)abstract.htmlI am going to talk about very popular combinatorial connection between ordinary and exponential generating functions which is
called cycle index function. I am going to define the combinatorial species according to the book "Theory of Species"
by Bergeron, Labelle, Leroux, and present their beautiful proof of the cycle index composition theorem.
The proof relies on the theory of symmetric functions in infinitely many variables.
This proof is a beautiful example of Grothendieck's concept: in order to prove something particular,
one should make a more general statement and prove it.
] 13/02/2018
Journées combinatoires de Bordeaux (12-14 février)06/02/2018
LIPN
Évaluation du laboratoire, exposés scientifiques 30/01/2018
Wenjie Fang Aspects énumératifs et bijectifs des cartes combinatoiresabstract.htmlLes cartes combinatoires, étant un modèle riche, portent plusieurs aspects : algébrique, géométrique, bijective, ... Dans cet exposé, je présente un ensemble de résultats et de connexions dans le domaine de l'énumération des cartes, obtenus à travers des aspects
différents. Nous verrons comment utiliser les outils algébrique, comme caractères du groupe symétrique et équations fonctionnelles, à énumérer les cartes. Nous verrons aussi comment étudier les autres objets dans la combinatoire, ici les intervalles du treillis de
Tamari, à travers de l'aspect bijectif des cartes.
] 30/01/2018
Mohab Safey El Din The quest of asymptotically fast algorithms for polynomial system solving over the realsabstract.htmlPolynomial systems arise in many areas of engineering
sciences and computer science. Most of the time, the end-user
expects some information about the real solution set of the system
under study. Algorithmic problems encompass which appear frequently
is to decide the existence of real solutions, compute sample points in
each connected component of the set under study, compute a description
of this set on some affine space or answer connectivity queries. All these
problems are NP-hard and, actually the best known complexities to solve
them are exponential in the number of variables. Moreover, because of the
non-linearity of the considered systems, reliable issues are
important. In this talk, I will give an overview of computer algebra
algorithms for solving these problems with a focus on those which
conciliate practical efficiency with asymptotically optimal
complexity.
] 24/01/2018
Jean-François Le Gall Colloquium LAGA (mercredi) : Géométrie aléatoire sur la sphèreabstract.htmlConsidérons une triangulation de la sphère choisie aléatoirement,
de manière uniforme, parmi toutes les triangulations ayant un
nombre fixé de faces (deux triangulations sont identifiées si
on passe de l'une à l'autre par un homéomorphisme direct
de la sphère). On munit l'ensemble des sommets de cette
triangulation de la distance de graphe usuelle. Nous montrons que,
quand le nombre de faces tend vers l'infini, l'espace métrique
ainsi obtenu, convenablement changé d'échelle, converge
en loi, au sens de la distance de Gromov-Hausdorff, vers un
espace métrique compact aléatoire appelé la carte brownienne.
Ce résultat, qui répond à un problème posé par Schramm,
reste vrai pour des classes beaucoup plus générales de graphes
plongés dans la sphère. La carte brownienne apparaît ainsi
comme un modèle universel de surface aléatoire, homéomorphe
à la sphère mais de dimension de Hausdorff égale à 4.
] 23/01/2018
Exposés d'équipes (Lionel, Frédérique, Olivier) 23/01/2018
Vincent Jugé Uniform generation of infinite concurrent runs: the case of trace monoidsabstract.html We introduce an algorithm for the uniform generation of infinite
runs in concurrent systems under a partial order probabilistic
semantics. Using trace monoids as concurrency models, we will first
focus on the notion of a uniform distribution on infinite traces in
general and on the simulation of such a distribution.
Then, we will introduce our algorithm, which aims at simulating a
uniform distribution in a distributed context. This algorithm outputs
on-the-fly approximations of a theoretical infinite run, the latter
being distributed according to the exact uniform probability measure.
The average size of the approximation grows linearly with the time of
execution of the algorithm, and the execution of the algorithm only
involves distributed computations, provided that some - costly -
precomputations have been done.
This presentation is based on a joint work with Samy Abbes.
] 16/01/2018
Pierre Rousselin Chute de dimension pour les marches aléatoires sur les arbres aléatoires [Slides.pdf ]abstract.htmlNous nous intéressons à différents modèles d'arbres aléatoires et aux marches aléatoires sur les sommets de tels arbres.
Dans le cas où la marche aléatoire est transiente, la marche part presque sûrement vers l'infini en empruntant un rayon aléatoire.
La loi de ce rayon est appelée la mesure harmonique sur le bord de l'arbre.
Un phénomène de chute de dimension se produit : cette mesure harmonique est presque sûrement concentrée sur une partie petite (au sens de la dimension de Hausdorff) du bord de l'arbre.
Autrement dit, les trajectoires de la marche aléatoires sont presque sûrement comprises dans un sous-arbre beaucoup plus fin que l'arbre original.
Cette théorie a été initiée par Russel Lyons, Robin Pemantle et Yuval Peres dans les années 1990.
Plus récemment, Nicolas Curien, Jean-François Le Gall, puis Shen Lin ont étudié ce phénomène sur un autre modèle d'arbres aléatoires.
Nous rappellerons leurs résultats et discuteront des généralisations sur lesquelles nous avons travaillé.
] [article ] [article ] 09/01/2018
Jordan Emme Produits de matrices aléatoires et application arithmétiqueabstract.htmlDans un travail en commun avec Pascal Hubert, nous étudions les lois limites de certains produits de matrices et en donnons une application arithmétique: On note s_2 la fonction somme des chiffres en base 2 et on considère, pour tous paramètres entiers a et d, la densité asymptotique mu_a(d) des ensembles d'entiers n tels que s_2(n+a)-s_2(n)=d. Pour tout a, mu_a est une mesure de probabilité sur Z. On démontre que pour toute mesure invariante ergodique sur {0,1}^N, et pour toute suite d'entiers (a_n) dont les décompositions en binaire décrivent les préfixes d'un point générique de cette mesure, mu_{a_n} vérifie un théorème de type limite centrée. Ce résultat est obtenu en calculant les moments de mu_{a_n} qui sont donnés par des produits de matrices aléatoires.
] 19/12/2017
thé combinatoire
pot de clôture, agrémenté de gâteaux et de False Beliefs in mathematics 19/12/2017
Juan Vera Lizcano Phase transition for the hard-core model in the 2-dimensional latticeabstract.html
The hard-core gas model is a natural combinatorial problem that has played an important role in the design of new approximate counting algorithms and for understanding computational connections to statistical physics phase transitions. For a graph G = (V, E) and a
fugacity t > 0, the hard-core model is defined on the set of independent sets of G where each independent set I has weight w(I) = |I|^t . The equilibrium state of the system is described by the Gibbs distribution in which each independent set I has probability ~
w(I).
A long-standing open problem to establish the critical fugacity t* for the hard-core gas model on the 2-dimensional integer lattice Z^2. In particular, t* is the conjectured critical point for the phase transition between uniqueness of infinite-volume Gibbs
measures on Z^2 when t < t* and non-uniqueness when t > t*. Empirical results identified the critical point t* ~ 3.79. The best known bounds show 2.538 < t* < 5.3646.
In this talk the techniques to obtain these bounds will be discussed. Special emphasis will be given to the lower bound, which is based on connections between the decay of correlations on the lattice and on its self-avoiding walk tree.
] 19/12/2017
Gérard Duchamp Free fields, automata and noncommutative geometry: a continuing trail (2/2) 15/12/2017
Alin Bostan Soutenance d'HDR : Computer algebra for lattice path combinatorics 12/12/2017
Pascal Weil A graph-based method to randomly generate subgroups of free groups [Slides.pdf ]abstract.htmlThe study of random algebraic objects sheds a different light on these objects, which complements the algebraic and the algorithmic points of view. When it comes to finitely generated subgroups of free groups, we have a remarkable graphical representation called
the Stallings graph: the Stallings graph of a subgroup H is a finite labeled graph uniquely associated with H, efficiently computed from a set of generators of H (say, given as reduced words), and from which one can efficiently compute many invariants of H.
I will discuss enumerating and randomly generating finitely generated subgroups of free groups, for the distribution given by Stallings graphs: for each positive integer n, one considers the finite number of subgroups whose Stallings graph has n vertices, and one
considers the uniform distribution on that set. This requires understanding the combinatorial structure of Stallings graphs, which are interesting objects per se. I will also exhibit natural properties of subgroups which are `generic' for this distribution.
This is joint work with F. Bassino (LIPN) and C. Nicaud (LIGM)
] [article ] 12/12/2017
Loïk Lhote Average-case analyses of multiple GCD algorithmsabstract.htmlThe computation of GCDs or inverse modulars is a basic operation
in Arithmetic or Cryptography. The analysis and the optimisation of
algorithms that compute GCDs is a speciality in Caen. In this talk, we
will introduce two multiple Gcd algorithms that are natural extensions
of the usual Euclid algorithm, and coincide with it for two entries. The
plain (or naive) algorithm was proposed by Knuth and performs successive
calls to the classical Euclid Algorithm. The Brun algorithm performs
Euclidean divisions, between the largest entry and the second largest
entry, and then re-orderings. This is the discrete version of a
multidimensional continued fraction algorithm due to Brun. We will
present the average--case analyses of the plain and the Brun algorithms.
Both analyses are very similar and we will prove that the mean number of
Euclidean divisions is linear with respect to the input size. However,
we show that the role of the dimension is different according to the
algorithm. The method relies on dynamical analysis, and is based on the
study of the underlying dynamical systems.
] 12/12/2017
Gérard Duchamp Free fields, automata and noncommutative geometry: a continuing trail (1/2) 06/12/2017
Journée MathStic
Journée "marches aléatoires" : Axel Bacher, Kilian Raschel, Arvind Singh et Niccolò Torri05/12/2017
Quentin de Mourgues Une approche combinatoire pour les dynamiques de type Rauzy (soutenance de thèse)abstract.htmlLa soutenance aura lieu le mardi 5 décembre à 12h45, en salle B017 du
LIPN (Paris 13) devant le jury composé de:
] 05/12/2017
Hoang Ngoc Minh On Drinfel'd associators 28/11/2017
Journée MathStic
Journée "flips" : Alexander Pilz, Thomas Budzinski, Lionel Pournin, Thomas Fernique21/11/2017
Christophe Vignat Séries génératrices pour la fonction "somme des chiffres en base b "abstract.htmlLa fonction sb (n ) est égale à la somme des chiffres qui composent la représentation de l'entier n en base b . De nombreuses séries associées à cette séquence ont été calculées, par exemple dans J.P. Allouche, J. Shallit, Sums of digits and the Hurwitz Zeta
function, Analytic Number Theory pp. 19-30, LNM 1434. On présentera de nouvelles séries génératrices associées à la suite sb (n ), ainsi que certains produits infinis. L'obtention de ces résultats utilise des outils rencontrés dans le
domaine du calcul symbolique et de la théorie des probabilités. Ce travail a été realisé en collaboration avec T. Wakhare.
] 21/11/2017
Karl Dilcher On the polynomial part of a restricted partition function [Slides.pdf ]abstract.htmlWe prove an explicit formula for the polynomial part of a restricted
partition function, also known as the first Sylvester wave. This is
achieved by way of some identities for higher-order Bernoulli polynomials,
one of which is analogous to Raabe's well-known multiplication formula for
the ordinary Bernoulli polynomials. As a consequence of our main result we
obtain an asymptotic expression of the first Sylvester wave as the
coefficients of the restricted partition grow arbitrarily large.
(Joint work with Christophe Vignat).
] 15/11/2017
Marie Albenque Convergence locale des cartes munies d'un modèle d'Ising (exposé au sém de proba) 15/11/2017
Christina Goldschmidt The scaling limit of the minimum spanning tree of the complete graph (exposé au sém de proba) 14/11/2017
thé combinatoire
False Beliefs in mathematics 14/11/2017
Michaël Rao Recherche exhaustive des pentagones convexes pavant le planabstract.htmlQuand on cherche à caractériser les formes convexes pouvant paver le
plan (en s’autorisant les rotations et miroirs), seul le cas des
pentagones restait ouvert. De 1918 à 2015, 15 différents types de
pentagones pouvant paver le plan ont été découverts. Je présente une
recherche exhaustive de tous les pentagones convexes pavant le plan, qui
permet de clore cette question. La preuve se sépare en deux parties: la
première montre, en utilisant la compacité, qu'on peut se limiter à un
ensemble de 371 familles, et la seconde est une recherche exhaustive
informatisée, pour chacune des 371 familles, qui ne trouve aucun nouveau
type de pentagones que les 15 types connus.
] 07/11/2017
Joseph Ben Geloun Énumeration dans les modèles de tenseurs : coefficients de Kronecker et algèbres de permutationsabstract.htmlLes invariants unitaires, ou contractions de tenseurs covariants et contravariants,
sont en bijection avec les graphes bi-partites colorés. Ces objets trouvent leur intérêt dans l'étude des cartes combinatoires
en dimension supérieure à deux. Je présenterai une autre connexion que peut avoir
le comptage de ces invariants avec la théorie de la représentation des groupes symétriques.
En particulier, je démontre que le nombre d'invariants de tenseurs de rang 3 est une somme de carrés de coefficients de Kronecker.
Ceci établit probablement un lien avec la théorie de la complexité.
D'autre part, en passant par l'algèbre du groupe symétrique, ces invariants peuvent être munis d'une structure algébrique.
Nous discutons les conséquences de l'existence d'une telle algèbre.
] 07/11/2017
Gérard Duchamp Noncommutative evolution equations: two-sided multipliers, initial conditions and asymptoticsabstract.htmlIn this talk, I will show tools and sketch proofs about Noncommutative Evolution Equations
(in particular, preparing Hoang Ngoc Minh's talk about associators). Starting from the very
simple setting of Noncommutative Formal Power Series with variable coefficients, we can
explore in a compact and effective (in the sense of computability) way the Hausdorff group
of Lie exponentials in particular the one linked to Hyperlogarithms (and then Polylogarithms)
and show some multiplicative renormalisations (as those of Drinfeld). Some parts of this work
are connected with Dyson series and take place within the project
"Evolution Equations in Combinatorics and Physics".
] 24/10/2017
Mathias Lepoutre Bijections pour marches sous-diagonales utilisant des diagrammes d'arc ouverts et des forêts de Schnyder [Slides.pdf ]abstract.htmlOn s'intéresse à deux problèmes d'énumération bijective, qui présentent une structure très similaire.
Le premier, énoncé par Bousquet-Mélou et Mishna en 2010, a été réduit par Elizalde en 2014 à trouver une bijection entre les chemins sous-diagonaux de longueur
paire utilisant des pas N,S,E,O finissant sur l'axe, et les excursions dans le quart de plan utilisant les mêmes pas.
Le deuxième, énoncé en 2015 par Burrill et al., consiste à montrer bijectivement que les diagrammes de partition ouverts sans 3-croisement
étendu sont énumérés par les nombres de Baxter.
Il se ramène au problème précédent en utilisant cette fois les pas N,S,E,O,NO,NS,EO,ES.
La similarité de ces deux problèmes nous amène à emprunter une démarche commune qui consiste à retirer les arcs ouverts
de la représentation par diagrammes définie par Chen et al. en 2005, pour se ramener à des excursions sous-diagonales marquées.
Au cours de la résolution de ces problèmes,
on utilisera les forêts de Schnyder pour démontrer la symétrie de certaines statistiques,
une méthode dont on verra qu'elle est en fait plus générale et permet dans plusieurs cas d'obtenir des symétries intéressantes.
] 24/10/2017
Gérard Duchamp Revêtements universels et équations differentielles non commutatives (d'après Cartier) 17/10/2017
Ilya Galanov On self-assembly of aperiodic tilingsabstract.htmlAperiodic tilings serve as a mathematical model for quasicrystals, such crystals that do not have any translational symmetry. Question about how quasicrystals grow still remains open. In this talk I will present the algorithm for growing defect free Penrose tilings using local rules based on paper “Growth rules for quasicrystals” by Joshua Socolar. And state necessary conditions for deterministic growth of cut-and-project aperiodic tilings using “defective seeds".
] 17/10/2017
Christian Lavault Propriétés des fonctions de Mittag-Leffler (3/3) 10/10/2017
Aléa Europe@Wien 03/10/2017
Thibault Godin Machines de Mealy, (semi-)groupes d'automate, problèmes de décision et génération aléatoire [Slides.pdf ]abstract.htmlDans cet exposé, je me propose de résumer les travaux que j'ai effectués pendant ma thèse sur les groupes d'automate. Tout d'abord, j'expliquerai comment les automates de Mealy (une classe spéciale de transducteurs) peuvent engendrer des (semi-)groupes et pourquoi
ces (semi-)groupes ont été intensément étudiés depuis les années 80. Je parlerai ensuite brièvement de trois de mes travaux, en commençant par la génération aléatoire de groupes finis, puis en parlant de la dynamique de l'action du groupe et enfin en étudiant le lien
entre certaines propriétés structurelles de l'automate et les caractéristiques du groupe qu'il engendre.
Dans tous ces exemples, j'espère réussir à souligner comment l'utilisation conjointe d'outils venant d'informatique théorique, de combinatoire et de théorie des
groupes permet une meilleure compréhension du sujet et l'obtention de nouveaux résultats.
Je terminerai en posant deux problèmes combinatoires qui pourraient intéresser les membres de l'assistance.
] 03/10/2017
Christian Lavault Propriétés des fonctions de Mittag-Leffler (2/3) 26/09/2017
Paul Mercat Un algorithme pour décider si un ensemble de Meyer substitutif est un coupé-projeté régulier ou nonabstract.htmlAprès avoir introduit ce que sont les quasicristaux, j'expliquai deux façons d'en construire : avec une description substitutive, et par coupé-projection. Le but de cet exposé sera de faire un lien entre ces deux constructions en se restreignant au cas d'un quasicristal de dimension 1 pour simplifier l'exposé. Plus précisément, étant donné une substitution associée à un nombre de Pisot, j'expliquai comment décider si le pavage autosimilaire correspondant peut aussi être décrit par un coupé-projeté régulier.
] 26/09/2017
Christian Lavault Propriétés des fonctions de Mittag-Leffler (1/3) 25/09/2017
Journée "Propriétés algorithmiques et asymptotiques des sous-groupes des groupes infinis" 19/09/2017
Valentin Bonzom Triangulations colorées en dimensions 3 et 4abstract.htmlLes triangulations colorées sont des espaces discrets formés par collage de briques élémentaires qui sont elles-mêmes formées de simplexes en dimension d. Ces briques élémentaires sont par exemple des polygones en dimension 2 et incluent les octaèdres en dimension 3. Les triangulations colorées visent ainsi le développement d'une nouvelle théorie qui intègrerait les cartes combinatoires, spécifiques à la dimension 2, dans un cadre théorique en dimension arbitraire. Je présenterai ces objets en expliquant qu'ils peuvent être représentés par des graphes aux arêtes colorées. Cela les rend particulièrement propices à l'analyse combinatoire, dans le but de les classifier combinatoirement à la manière du genre en dimension 2 et de les énumérer. Je définirai une notion généralisant la planarité en dimension supérieure et je présenterai un système d'équations portant sur les fonctions génératrices de triangulations colorées, qui généralise les équations de Tutte/Schwinger-Dyson des cartes. Selon le temps restant et les gouts de l'auditoire, je pourrai présenter des résultats soit en dimension 3 lorsque les briques élémentaires sont homéomorphes à des boules, soit en dimension 4 où il existe des régimes dans les classes d'universalité des arbres, des cartes planaires et des arbres de cartes mélangeant les deux.
] 19/09/2017
Hoang Ngoc Minh Décalage des centres 05/09/2017
Michael Wallner Limit laws for lattice paths with catastrophesabstract.htmlIn queuing theory, it is usual to have some models with a "reset" of the queue. In terms of lattice paths or random walks, it is like having the possibility of jumping from any altitude to zero. These objects have the interesting feature that they do not have the
same intuitive probabilistic behaviour as classical Dyck paths (the typical properties of which are strongly related to Brownian motion theory). In this talk we will quantify some relations between these two types of paths.
Starting from an a priori not expected continued fraction
(for which we give a bijective proof, and an analytic proof),
we prove several formulae for related combinatorial structures conjectured
in the On-line Encyclopedia of Integer Sequences.
We also derive limit laws for parameters like the number of returns to zero or the size of an average catastrophe.
We end with some considerations on uniform random generation.
[Joint work with Cyril Banderier]
] 05/09/2017
Gérard Duchamp Groupes de Galois des équations différentielles non commutatives et décalage des centres 18/07/2017
Medhi Naima Arbres de synchronisation et théorie de la concurrenceabstract.htmlNous nous intéressons aux structures mathématiques sous-jacentes des programmes concurrents et parallèles.
L'idée est de modéliser des programmes concurrents à l'aide d'abres étiquettés croissants.
Nous pouvons ensuite réaliser une étude combinatoire sur ces structures, en déduire certaines propriétés et faire une génération aléatoire uniforme
de programmes concurrents qui peut servir dans le cadre du model-checking.
] 18/07/2017
Youssef Abdelaziz Roger Apéry et l'irrationalité de zêta(3) 18/07/2017
Jean Peyen Analyse de paramètre dans les lambda termes linairesabstract.htmlNous nous intéresserons d'abord au comportement asymptotique du nombre de variables libres des lambda-termes linéaires uniformément générés.
Nous discuterons ensuite de la génération aléatoire de lambda-termes linéaires clos via l'utilisation d'un GPU.
] 11/07/2017
Lionel Pournin Sur le diamètre des polytopes en nombres entiersabstract.htmlLe diamètre des polyèdres est une borne théorique sur la complexité de l'algorithme du simplexe. Pour cette raison, il est habituellement estimé en fonction de la dimension d du polyèdre et du nombre n de ses facettes.
Dans le cas des polytopes en nombres entiers contenus dans l'hypercube [0,k ]d k de l'hypercube cube et sa dimension d . Cet exposé présente des résultats récents
sur le plus grand diamètre δ(d,k ) de tels polytopes. Plusieurs de ces résultats seront présentés et discutés. Ces résultats seront mis en perspective avec la conjecture de Hirsch (maintenant infirmée) et avec des travaux de Thiele, Balog et Bàràny et
Acketa et Žunic sur les polygones en nombres entiers contenus dans le carré [0,k ]2 .
] 04/07/2017
Maciej Bendkowski Quantitative aspects and random generation of lambda-termsabstract.htmlIn our overview talk, we present a quantitative analysis of lambda calculus and combinatory logic under various combinator bases, focusing on the asymptotic properties of both computational models, such as normalisation or typeability. We discuss utilised analytic
methods, their limitations and current challenges. Finally, we discuss effective random sampling techniques, in particular Boltzmann models, and their application in automated software verification tools.
] [article ] 27/06/2017
Vincent Delecroix Compter les méandresabstract.htmlUn méandre est une configuration d'intersections de deux courbes sur la sphère. Leur comptage résiste depuis longtemps à l'assaut des physiciens théoriciens, des informaticiens et des mathématiciens. Nous savons depuis longtemps qu'il existe un exposant de croissance exponentielle (pour des raisons de sous-additivité) mais pas beaucoup plus... Dans cet exposé, je présenterai comment obtenir des asymptotiques de comptage de méandres lorsqu'on contraint la combinatoire. Dans les cas que nous considérons, l'asymptotique est polynomiale et non plus exponentielle. Ces résultats nouveaux obtenus par des méthodes de théorie ergodique n'éclairent pas, à priori, le problème du comptage non contraint. (travail en commun avec E. Goujard, A. Zorich et P. Zograf)
] [article ] [article ] 13/06/2017
Samuele Giraudo Grammaires à bourgeons [Slides.pdf ]abstract.htmlLes opérades colorées permettent de généraliser la notion de grammaire
non contextuelle de façon à décrire des familles d'objets combinatoires
variées (dont les arbres, englobant de ce fait les grammaires d'arbres
régulières). Nous allons introduire ces grammaires, appelées grammaires
à bourgeons, et expliquer comment il est possible de considérer des
séries formelles sur les opérades colorées. Ce dernier point offre des
outils pour le dénombrement. Dans ce contexte, nous introduisons
plusieurs produits sur l'espace de ces séries : un produit pré-Lie, un
produit de composition associatif et deux analogues de l'étoile de
Kleene.
] [article ] 13/06/2017
Samuele Giraudo Opérades des cliques décorées [Slides.pdf ]abstract.htmlNous proposons une construction fonctorielle de la catégorie des magmas
unitaires vers celle des opérades non symétriques. Cette construction
munit l'espace des configurations de diagonales décorées dans les
polygones d'une structure d'opérade. On obtient ainsi diverses nouvelles
opérades sur des sous-familles particulières de tels polygones :
configurations sans croisement, configurations non imbriquées,
configurations de Motzkin, etc. Nous montrons aussi comment cette
construction permet de donner des définitions alternatives d'opérades
déjà connues comme l'opérade des simples et doubles multi-tiles
(provenant de la théorie des langages) et l'opérade de gravité.
] [article ] 06/06/2017
Akhilesh Parol Multizeta values and Apéry-like sums [Slides.pdf ] 06/06/2017
Hoang Ngoc Minh Le domaine des polylogarithmes (The domain of Li)abstract.htmlThe polylogarithm map Li can be extended partly to some series. In this talk, we
examine the algebra generated by the image of Li of a particular family of series
that we call "Star of the plane". We discuss the basis of the algebra as a module
and the characters of this algebra. We also prove the linear independence of the
usual polylogarithms over this algebra.
] 30/05/2017
Pierre Lairez Calcul des périodes : applications aux sommes binomiales et au volume d'ensembles semi-algébriquesabstract.htmlL'étude des intégrales de fonctions algébriques est très fructueuse en géométrie algébrique, comme l'illustre,
par exemple, les travaux d'Euler sur les intégrales elliptiques. Les applications aux calculs effectifs sont moins connues. J'en présenterai quelques
unes. Plus précisément, je vais m'intéresser aux « périodes », c'est le résultat de l'intégration
sur un cycle d'une fractions rationnelle en plusieurs variables. Je montrerai comment les calculer, sous la forme d'équations différentielles,
et j'expliquerai deux applications à des problèmes bien différents : la démonstrations automatiques d'identités entre sommes binomiales
et le calcul du volume de certains ensembles semi-algébriques (i.e., définis par un ensemble d'inégalités polynomiales).
] 30/05/2017
Hoang Ngoc Minh Autour des associateurs (séance de calcul)abstract.htmlThis talk concerns the resolution of $KZ_3$ and our recent
results on combinatorial aspects of zeta functions,
$\{\zeta(s_1,\ldots,s_r)\}_{s_1,\ldots,s_r\in{\mathbb C}^r}$.
In particular, we describe the action of the differential Galois group
of $KZ_3$ on the asymptotic expansions of its solutions leading to
a group of associators which contains the associator $\Phi_{KZ}$.
Non trivial expressions of an associator with rational coefficients
is also explicitly provided, based on the algebraic structures and
the singularity analysis of
the polylogarithms, $\{{\rm Li}_{s_1,\ldots,s_r}\}_{s_1,\ldots,s_r\in{\mathbb C}^r}$,
and the harmonic sums, $\{H_{s_1,\ldots,s_r}\}_{s_1,\ldots,s_r\in{\mathbb C}^r}$.
] 23/05/2017
Thierry Monteil Magouilles diverses pour les machines à signauxabstract.htmlLes machines à signaux sont un modèle de calcul déterministe dont espace et temps sont continus.
Si les accumulations d'événements sont interdites, ce modèle est connu
pour être équivalent au modèle de BlumShubSmale linéaire. Nous
construirons dans ce cadre un oracle universel optimal (en nombre de
vitesses et de paramètres irrationnels). Nous verrons comment jouer au
billard permet semi-décider l'algébricité d'un nombre réel alors que c'est
impossible dans le modèle BSS-linéaire. Nous verrons comment modifier
légèrement le modèle pour obtenir un modèle équivalent au modèle BSS
standard.
Lorsque l'on permet aux accumulations d'événements de produire un signal,
nous verrons, en jouant sur l'alternance discret/continu, comment
construire des machines dont le pouvoir dépasse largement les modèles de
calcul usuels, en particulier, nous construirons
une "courbe de Peano" c'est a dire une surjection de [0,1] dans
[0,1]^2.
un "oracle universel continu", c'est à dire un machine à un paramètre
M(p) telle que toute suite N->[0,1] est generèe un certain M(p).
une "fonction analytique universelle", c'est à dire une machine avec
2 parametres t,x telle que pour toute fonction analytique f de rayon de
convergence >1, il existe t tel que f(x)=M(t,x) pour tout x dans [-1,1],
en particulier, on peut calculer les fonctions exp(x), sin(), en déplaçant
un curseur.
aussi, on peut prendre en compte la géométrie du modèle dans la
formulation même de ce que peut "calculer" (ou "dessiner") une machine,
pas seulement un booléen, un entier ou un réel comme dans le cas discret.
Étant donnée une machine M, si certains types de collisions sont coloriés
en rouge, l'ensemble de leurs accumulations au temps 1 est un compact. Il
se trouve que cette restriction est la seule : il existe une machine à un
parametre M(p) telle que pour tout compact K inclus dans [0,1], il existe
p dans [0,1] tel que l'ensemble des accumulations rouges de M(p) au temps
1 est K.
L'exposé sera informel et sa compréhension ne nécessitera pas de prérequis.
] 23/05/2017
Hoang Ngoc Minh Autour des associateursabstract.htmlThis talk concerns the resolution of $KZ_3$ and our recent
results on combinatorial aspects of zeta functions,
$\{\zeta(s_1,\ldots,s_r)\}_{s_1,\ldots,s_r\in{\mathbb C}^r}$.
In particular, we describe the action of the differential Galois group
of $KZ_3$ on the asymptotic expansions of its solutions leading to
a group of associators which contains the associator $\Phi_{KZ}$.
Non trivial expressions of an associator with rational coefficients
is also explicitly provided, based on the algebraic structures and
the singularity analysis of
the polylogarithms, $\{{\rm Li}_{s_1,\ldots,s_r}\}_{s_1,\ldots,s_r\in{\mathbb C}^r}$,
and the harmonic sums, $\{H_{s_1,\ldots,s_r}\}_{s_1,\ldots,s_r\in{\mathbb C}^r}$.
] 16/05/2017
Yann Chevaleyre Thé combinatoire accompagné d'un petit problème de combinatoire géométrique issu de l'apprentissage 16/05/2017
Yann Ponty Génération aléatoire de marches 2D positivesabstract.htmlLes marches aléatoires 2D, composés d'un ensemble fini de pas élémentaires et
restreintes au quadrant positif, forment des classes combinatoires dotées de
structures typiquement complexes, et admettant une grande variété de
comportements asymptotiques.
En collaboration avec Jérémie Lumbroso (Princeton, USA) et Marni Mishna (SFU,
Canada), nous nous intéressons à la génération aléatoire uniforme de marches
d'une taille n donnée, à partir de l'ensemble des pas élémentaires. Notre
principal résultat consiste en un algorithme de rejet, qui remplace le quart de
plan par un demi-plan bien choisi. On se ramène alors à la génération aléatoire
de marches 1D composées de pas généralement irrationnels, et pour lesquels une
génération uniforme est possible en temps polynomial à partir d'une famille de
grammaires non-contextuelles. Un résultat de Garbit et Raschel démontre ensuite
l'existence d'un demi-plan tel que l'espérance du nombre de tirages dans le
demi-plan est polynomiale, mais une analyse plus fine de la complexité de cette
approche soulève des questions en combinatoire (analytique) des marches 1D/2D
et des spécifications algébriques. Cette présentation consiste en une version
étendue d'un exposé présenté à GASCOM 2016.
] 09/05/2017
Tom Denat Random graphs and average-case analysis of NP-complete problems [Slides.pdf ] [article ] 02/05/2017
Alice Héliou Mots minimaux absents 02/05/2017
Hoang Ngoc Minh The algebra of Kleene stars of the plane and polylogarithms [article ] 25/04/2017
Nicolas Behr The rule algebra framework - a diagram-algebraic approach to stochastic rewriting abstract.htmlI will give an overview and report on the latest results of the so-called rule algebraic approach to stochastic rewriting systems [1,2]. Besides a general (high-level) introduction to the mathematical concepts, the focus of the talk will be on the practical implications in terms of efficiently analyzing rewriting systems. In particular, I will compare the traditional approaches to analyzing chemical reaction systems (aka discrete graph rewriting systems) to analytically tractable cases of stochastic graph rewriting systems, such as the preferential attachment model. Amongst the novel results, the combinatorial conversion and disassociator dynamics theorems introduced in detail in the morning session will be mentioned, as well as perspectives in terms of restricted rewriting systems.
] [article ] 25/04/2017
Nicolas Behr Combinatorial conversion and disassociator dynamics for stochastic rewriting systems [abstract.pdf ] 18/04/2017
Thomas Dreyfus Holonomie et non-holonomie des marches dans le quart de planabstract.htmlL'étude des marches dans le quart de plan a fait ces dernières années l'objet de nombreuses avancées,
aussi bien par des méthodes de combinatoire, de théorie des probabilités, de théorie du potentiel, de calcul formel...
Il reste de nombreux problèmes ouverts, comme notamment mieux comprendre
pourquoi certaines marches sont dénombrées par des séries génératrices algébriques,
d'autres par des séries D-finies (holonomes),
tandis que d'autres (a priori très "proches") aboutissent à des séries non différentiellement algébriques.
Nous montrerons comment la théorie de Galois
(et notamment ses variantes pour des équations aux différences),
ainsi que des éléments d'analyse complexe (paramétrisation de courbes par fonctions elliptiques)
nous a permis d'avancer sur ces questions.
[travail joint avec Michael Singer, Julien Roques, Charlotte Hardouin]
] [article ] 18/04/2017
Gérard Duchamp Noncommutative evolution equations: twosided multipliers, initial conditions and asymptotics 11/04/2017
Nicolas Gachadoit Utilisation avancée de Maple : calcul parallèle et interfaçage avec des bibliothèques externesabstract.htmlMaple possède plusieurs milliers de fonctions, mais certains calculs spécifiques peuvent nécessiter l'utilisation de bibliothèques externes. Par ailleurs, les ordinateurs n'évoluent plus tellement dans le sens d'une augmentation de la fréquence des processeurs mais
dans le sens d'une augmentation du nombre de cœurs de calcul.
Cette présentation détaillera les fonctionnalités de Maple permettant de réaliser des calculs parallèles et de s'interfacer avec du code écrit dans d'autres langages.
] 04/04/2017
Mireille Régnier Accurate prediction of the statistics of repetitions in random sequencesabstract.htmlRepetitive patterns in genomic sequences have a great biological significance and also algorithmic implications. Analytic combinatorics allow to derive formula for the expected length of repetitions in a random sequence. Asymptotic results, that generalize previous
works on a binary alphabet, are easily computable. Simulations on random sequences show their accuracy. As an application, the sample case of Archaea genomes illustrates how biological sequences may differ from random sequences.
] 28/03/2017
Sergey Dovgal Phase Transition Threshold for Random Graphs and 2-SAT using Degree Constraintsabstract.htmlWe show that by restricting the degrees of the vertices of a graph to an arbitrary set Δ, the threshold α(Δ)
of the phase transition for a random graph with n vertices and m = α(Δ).n edges can be either accelerated (e.g.,
α(Δ) approx 0.38 for Δ = {0,1,4,5}) or postponed (e.g., α(Δ) approx 0.95 for Δ={1,2,50})
compared to a classical Erdős–Rényi random graph where α(N)=1/2.
We investigate different graph statistics inside the critical window of transition (planarity, diameter, longest path...).
We apply our results to a 2-SAT model with restricted literal degrees: the number of clauses that each literal
is incident to belongs to the set Δ. We prove a lower bound for the probability that a formula with n variables
and m=2.α(Δ) n clauses is satisfiable. This probability is close to 1 for the subcritical
regime m=2.α.n.(1-μ.n-1/3 ), μ to ∞ and improves/generalizes the lower bound of Bollobás, Borgs, Chayes, Kim, and Wilson.
This shows how the phase transition threshold for 2-SAT moves if we change the degrees of the literals.
Joint work with Vlady Ravelomanana.
] [article ] 21/03/2017
Journées Aléa 14/03/2017
Xavier Goaoc Géométrie combinatoire : densité d'hypergraphes et méthode probabilisteabstract.html Un hypergraphe à n sommets dont aucune projection sur k sommet n'est complète a au plus O(n^{k-1}) arêtes. Ce résultat, découvert simultanément par Sauer, Vapnick-Chervonenkis et Perles-Shelah au début des années 1970, est fondamental en apprentissage. En géométrie combinatoire et algorithmique, il permet souvent de contrôler la complexité (globale) d'une structure par sa "densité" locale. J'introduirai à ce mécanisme avant de présenter quelques extensions récentes, obtenues conjointement avec Boris Bukh (https://arxiv.org/abs/1701.06632), qui permettent un controle plus fin de la complexité. L'exposé ne supposera aucune connaissance préalable et un des ingrédients sera une construction probabiliste.
] [article ] 07/03/2017
CALIN
réunion d'équipe pour le rapport scientifique 07/03/2017
Christophe Tollu TBA 21/02/2017
Nicolas Macé Conductivité des quasicristaux et pavages apériodiques [Slides.pdf ] [article ] 21/02/2017
Christian Lavault Fonctions de type Mittag-Leffler et calcul fractionnaire 07/02/2017
Éric Fusy Bijections for planar maps with boundaries [Slides.pdf ] 07/02/2017
Gérard Duchamp Polylogarithms and fields of germs 31/01/2017
Veronica Guerrini The neighbours of Baxter numbers [Slides.pdf ]abstract.htmlBaxter numbers are a well known number sequence enumerating Baxter permutations and several other combinatorial objects. In this talk, we define a new class of objects called Slicings of parallelogram polyominoes counted by Baxter numbers that enables us to find a
continuum from Catalan structures to Baxter structures. This continuum is established by means of a new succession rule (i.e. generating tree) associated with Schröder numbers, that interpolates between the known succession rules for Baxter and Catalan
numbers. Then, similarly we consider a generalization for the Baxter succession rule that forms a link between Baxter numbers and Factorial numbers. Such succession rule defines semi-Baxter numbers, which result to count plane permutations, whose enumeration was set
as an open problem by Bousquet-Mélou and Butler, and inversion sequences avoiding (210,100), as conjectured by Martinez and Savage.
] 25/01/2017
Journées combinatoires de Bordeaux (25-27 janvier)24/01/2017
Gérard Duchamp Polylogarithms and solutions of KZ3 + programme février-mars 17/01/2017
Workshop on Large Random Structures in Two Dimensions (IHP 16-20 janvier)17/01/2017
Gérard Duchamp Non-commutative differential equations, topology and algebra (3/3) (interactive). 10/01/2017
Youssef Abdelaziz Combinatorial physics, hypergeometric functions and differential equations [Slides.pdf ] [article ] 10/01/2017
Philippe Duchon Permutations aléatoires et cycles courts (via des arbres de génération)abstract.htmlTirer une permutation aléatoire uniforme de taille n n'est pas bien
difficile, et on sait assez bien à quoi c'est censé ressembler. Qu'en
est-il si on souhaite imposer des restrictions sur le type cyclique?
Il n'est pas bien difficile non plus de tirer une permutation
aléatoire ayant un nombre prédéterminé de points fixes - il suffit de
savoir tirer un dérangement, et à grande taille, près de 37% des
permutations sont des dérangements. On a donc facilement un algorithme
qui va nécessiter en moyenne O(n) tirages d'entiers aléatoires d'ordre
O(n).
Dans ce travail en commun avec Romaric Duvignau (EJC, 2016),
nous montrons comment cela peut être fait avec n+O(1) tirages en
moyenne, par un rejet anticipé. Cela est possible grâce à la
construction d'un arbre de génération pour les permutations, qui a la
particularité de "fixer" très rapidement, et aussi vite qu'il est
possible, le nombre de points fixes. Comme conséquences faciles, on a
alors des algorithmes tout aussi efficaces pour tirer des permutations
aléatoires avec un nombre prescrit de points fixes. Le passage de
"points fixes" à "cycles d'une longueur k donnée" est possible, mais
sensiblement moins élégant.
] 10/01/2017
Gérard Duchamp Non-commutative differential equations, topology and algebra (2/3) (characters). 03/01/2017
Gérard Duchamp Séries doubles et structures de données 03/01/2017
Hoang Ngoc Minh Séance d'ouverture 2017 : Polylogarithms and harmonic sums with complex multi-indices. 20/12/2016
Gérard Duchamp Non-commutative differential equations, topology and algebra (1/3) 13/12/2016
Journée MathStic
Modèles de dimères : Vincent Beffara , Benoît Laslier , Cédric Boutillier , Béatrice de Tilière 09/12/2016
Quoc Hoan Ngo Double regularization of polyzetas at negative multi-indices and rational extensions (soutenance de thèse)abstract.htmlIn this PhD thesis are studied the polylogarithms and the harmonic sums at non-positive (i.e., weakly negative) multi-indices. General results about these objects in relation with Hopf algebras are pr ovided. The technics exploited here are based on the
combinatorics of noncommmutative generating series relative to the Hopf phi-huffle algebra. Our work will also propose a global process to renormalize divergent polyzetas. Finally, we will apply these ideas to non-linear dynamical systems with singular inputs.
The jury will be composed of:
Gérard Duchamp, Hoang Ngoc Minh (directeurs),
Sylvie Paycha, Dominique Manchon (rapporteurs), Karol Penson, Vincent Rivasseau, Loic Foissy, Christophe Tollu.
] 09/12/2016
Van Chiên Bui Développement asymptotique des sommes harmoniques (soutenance de thèse)abstract.htmlEn abordant les nombres spéciaux comme les sommes harmoniques ou les polyzêtas sous leur aspect combinatoire, nous introduisons d'abord la définition d'un produit entre mots, dit produit de quasi-mélange q-déformé, une généralisation des produits de mélange et de quasi-mélange, ce qui nous permet de construire des structures complètes d'algèbre de Hopf en dualité. En même temps, nous construisons des bases en dualité, contenant des bases de transcendance associées aux mots de Lyndon, et des formules explicites sur lesquelles les sommes harmoniques, les polyzêtas ou les polylogarithmes sont
indexés et représentés par la factorisation de la série génératrice noncommutative diagonale. De cette façon, en identifiant les coordonnées locales, nous trouvons des relations polynomiales homogènes, en poids, entre les polyzêtas indexés par ces bases.
Enfin, nous déterminons les développements asymptotiques des sommes harmoniques, indexées aussi par ces bases, grâce à leur série génératrice et à la formule d'Euler Maclaurin.
Pour accompagner cette étude théorique, nous proposons des algorithmes et un package en Maple afin de calculer des bases,
la structure des polyzêtas et des développements asymptotiques des sommes harmoniques.
Le jury sera composé de
Gérard Duchamp, Hoang Ngoc Minh,
(co-directeurs),
Jacky Cressson, Loïc Foissy,
(rapporteurs),
Sylvie Paycha,
Joris van der Hoeven,
Daniel Barsky,
Christophe Tollu (examinateurs).
] 06/12/2016
Tatiana Starikovskaya Streaming and communication complexity of Hamming distance [Slides.pdf ]abstract.htmlWe will discuss the complexity of one of the most basic problems in pattern matching, that of approximating the Hamming distance. Given a pattern P of length n the task is to output an approximation of the Hamming distance (that is, the number of mismatches) between P and every n-length substring of a longer text. We provide the first efficient one-way randomised communication protocols as well as a new, fast and space efficient streaming algorithm for this problem.
] 06/12/2016
Van Chiên Bui Développement asymptotique des sommes harmoniques (3ème partie) 06/12/2016
Quoc Hoan Ngo Double régularisation des polyzêtas en les multi-indices négatifs et extensions rationnelles (3ème partie) 02/12/2016
Alexandra Ugolnikova Pavages aléatoires (soutenance de thèse)abstract.htmlB0;136;0cDans cette thèse nous étudions deux types de pavages : des pavages par une paire de
carrés et des pavages sur le réseau tri-hexagonal (Kagome). Nous considérons différents
problèmes combinatoires et probabilistes. Nous commençons par le cas des carrés 1 × 1
et 2 × 2 sur des bandes infinies de hauteur k et obtenons des résultats sur la proportion
moyenne des carrés 1 × 1 pour les cas planaire et cylindrique pour k ≤ 10. Nous
considérons également des questions d’échantillonnage et comptage approximatif. Pour
obtenir un échantillon aléatoire nous définissons des chaînes de Markov pour les pavages
par des carrés et sur le réseau Kagome. Nous montrons des bornes polynomiales pour
le temps de mélange pour les pavages par des carrés 1 × 1 et s × s des régions n × log n
et les pavages Kagome des régions en forme de losange. Nous considérons aussi des
chaines de Markov avec des poids λ sur les tuiles. Nous montrons le mélange rapide
avec des conditions spécifiques sur λ pour les pavages par des carrés 1 × 1 et s × s et
pavages Kagome. Nous présentons des simulations qui suggèrent plusieurs conjectures,
notamment l’existence des région gel´ees pour les pavages aléatoires par des carrés et sur
le réseau Kagome des régions avec des bords non plats.
Le jury se composera de Thomas Fernique (directeur),
Béatrice de Tilière, Éric Rémila (rapporteurs),
et de Frédérique Bassino, Olivier Bodini,
Ana Bušić,
Pavel Kalouguine.
] 29/11/2016
Olivier Bodini Une analyse asymptotique des polyominos digitalement convexesabstract.htmlDans cet exposé, nous montrerons comment des techniques élémentaires (transformées de Mellin) en combinatoire analytique permettent d'obtenir des résultats assez surprenants sur les polyominos. En particulier, si l'on savait correctement énumérer les polyominos digitalement convexes, nous saurions si l'hypothèse de Riemann est vraie !
] 29/11/2016
Van Chiên Bui Développement asymptotique des sommes harmoniques (2ème partie) 29/11/2016
Quoc Hoan Ngo Double régularisation des polyzêtas en les multi-indices négatifs et extensions rationnelles (2ème partie) 22/11/2016
Quoc Hoan Ngo Double régularisation des polyzêtas en les multi-indices négatifs et extensions rationnelles. 22/11/2016
Réunion d'équipe 22/11/2016
Van Chiên Bui Développement asymptotique des sommes harmoniques 17/11/2016
Journée MathStic
Croissance-fragmentation : Benjamin Dadoun (Zurich), Marie Doumic (INRIA), Igor Kortchemski (X), Quan Shi (P13) 15/11/2016
Quoc Hoan Ngo An interface between physics and number theory [abstract.pdf ] 15/11/2016
Samuel Petite Restrictions sur le groupe d'automates cellulaires préservant un sous-shift fixéabstract.htmlUn sous shift est un ensemble fermé de suites sur un alphabet fini, invariant par décalage (le shift). L'ensemble des automates cellulaires préservant ce sous shift est en général un groupe dénombrable compliqué. Nous présenterons dans cet exposé un survol des
différentes restrictions sur ces groupes pour les sous-shift d'entropie nulle.
] 15/11/2016
Suzy Maddah On Generalized Hypergeometric Solutions of Linear Differential Systems of First Orderabstract.htmlIn this talk, we consider linear differential systems of first order (equivalently linear differential equations of arbitrary order), and we question whether they can be solved in terms of generalized hypergeometric functions. This question is motivated by the many
properties of the latter which arise in physics and combinatorics. It has been tackled in the literature for second-order differential equations, namely Bessel's, Whittaker's, Kummer's, and Gauss's. We propose a new algorithm which surpasses the restrictions on the
dimension of the system, and equivalently on the order of the equation. This is joint work with Frédéric Chyzak.
] 08/11/2016
30 ans du LIPN 25/10/2016
Vincent Pilaud Réalisations géométriques des complexes d'accordéonsabstract.htmlSoient 2n points en position convexe alternativement colorés rouges et bleus, et soit D une dissection de l'enveloppe convexe des points rouges. Une diagonale entre deux points bleus est un D-accordéon si les arêtes de D qu'elle croise forment un accordéon. Le
complexe d'accordéons de D est le complexe simplicial formé des ensembles de D-accordéons qui ne se croisent pas. Par exemple, le complexe d'accordéons d'une triangulation est un associaèdre, et celui d'une quadrangulation a été étudié par Baryshnikov et
Chapoton. Ces complexes ont été introduits récemment par Garver et McConville dans un langage dual. Dans cet exposé, nous donnerons des réalisations géométriques de ces complexes simpliciaux, basées sur de fortes analogies avec les algèbres amassées de type
fini. Lorsque D est une triangulation ayant des triangles internes, nous obtenons en particulier de nouvelles réalisations de l'associaèdre. Cet exposé est basé sur des travaux en commun avec Christophe Hohlweg (UQAM, Montréal), Thibault Manneville (LIX, École Polytechnique) et Salvatore Stella (Univ. la Sapienza, Rome).
] 25/10/2016
Christophe Tollu Sur les catégories additives et abéliennes (2/2) 18/10/2016
Johan Nilsson Counting square tilingsabstract.htmlWe consider tilings of a rectangle with squares tiles of size 1x1 and 2x2. We present a method to calculate the number of such tilings via matrix multiplication, where we optimize the number of multiplication needed and reduce the space required for the matrix
multiplication by dynamically generate the matrices involved.
] 18/10/2016
Van Chiên Bui Développement asymptotique des sommes harmoniques 11/10/2016
Gérard Duchamp Non-commutative differential equations and (some) geometrical hintsabstract.htmlOn prendra appui sur les intégrales itérées des systèmes
fuschsiens pour proposer une théorie des équations différentielles
non-commutatives. Plusieurs surprises et cadeaux nous attendent
dans cette exploration.
] 11/10/2016
Christophe Tollu Sur les catégories additives et abéliennes (1/2) 06/10/2016
Nicolas Rolin De l'usage des opérateurs en combinatoire : construction, analyse et génération aléatoire (soutenance de thèse)abstract.htmlOn étudie en combinatoire les objets munis d'une taille (la taille dans le cadre informatique peut se traduire par exemple par la mémoire occupée par l'objet).
On appelle classe combinatoire un ensemble d'objets qui pour toute taille possède un nombre fini d'éléments.
On peut par exemple considérer les textes régis par une certaine grammaire, dans ce cas la taille est le nombre de caractères, ou des arbres avec comme taille le nombre de nœuds.
Une méthode naturelle pour décrire les classes, la méthode symbolique, consiste à décomposer les objets en sous-objets plus élémentaires à l'aide d'opérateurs (tels que l'union disjointe, le produit cartésien,...).
On peut ensuite traduire ces décompositions sur des séries formelles.
Le premier volet de résultats présentés dans cette thèse traite de la méthode symbolique et de son utilisation. On y présente des résultats asymptotiques sur des modèles d'arbres croissants issus de la théorie de la concurrence,
puis une discussion sur comment décomposer certains opérateurs en réplications élémentaires.
Le deuxième volet de résultats s'intéresse au sujet de la génération aléatoire uniforme d'objets dans une classe donnée.
On montre tout d'abord comment générer des structures croissantes en adaptant les méthodes de génération récursive classiques aux opérateurs de produit croissant.
On présente ensuite des résultats sur la génération de Boltzmann, avec une comparaison quantitative de deux méthodes, puis une extension permettant de conserver les propriétés d'uniformité de la génération en utilisant des approximations.
] 04/10/2016
Marc Mezzarobba Évaluation multi-précision rigoureuse de fonctions D-finies en Sage [Slides.pdf ]abstract.htmlJe présenterai une implémentation en développement d'algorithmes
d'évaluation numérique de fonctions D-finies (c.-à-d. solutions
d'équations différentielles linéaires à coefficients polynomiaux), pour
le logiciel de calcul formel libre SageMath. Ce nouveau package a
vocation à remplacer NumGfun, un package un peu similaire pour Maple que
j'ai présenté au séminaire CALIN il y a quelques années. Si le temps le
permet, je dirai aussi quelques mots des algorithmes originaux utilisés.
La fonctionnalité centrale de ce code est le « prolongement analytique
numérique » d'une fonction D-finie, qui fournit une approximation de la
matrice envoyant un jeu de conditions initiales en un point donné du
plan complexe sur les conditions « initiales » qui définissent la même
fonction au voisinage d'un autre point. Le prolongement analytique
numérique permet de calculer des valeurs ou encore des approximations
polynomiales de fonctions D-finies n'importe où sur leur surface de
Riemann, des matrices de monodromie d'opérateurs différentiels, etc. Le
code traite complètement le cas limite important de conditions initiales
généralisées données en un point singulier régulier de l'opérateur. Il
peut donc être utilisé pour calculer des matrices de connexion entre
singularités régulières, ce qui est utile notamment en combinatoire
analytique. Par ailleurs, il s'agit d'une implémentation rigoureuse, au
sens où elle renvoie des intervalles qui (sauf bug !) contiennent à coup
sûr le résultat mathématique exact.
] 04/10/2016
Gérard Duchamp TBA 27/09/2016
Quan Shi Random recursive trees and growth-fragmentationsabstract.htmlGrowth-fragmentation processes describe the evolution of particles that grow and divide as time proceeds. Previous studies on growth-fragmentations have mostly focused on the self-similar case. In this talk we introduce a new class of growth-fragmentations, called Ornstein- Uhlenbeck type growth-fragmentations. Loosely speaking, the size of each fragment evolves according to the exponential of a Lévy driven Ornstein-Uhlenbeck type process. This model is partly motivated by the work of Bertoin and Baur (EJP. 2015) which shows that such processes arise naturally in dynamical percolation on an infinite random recursive tree.
] 27/09/2016
Hoang Ngoc Minh Trans-series and a nice story. 20/09/2016
Joseph Ben Geloun Counting observables of colored tensor modelsabstract.htmlColored tensor models generate Feynman graphs representing discrete geometries.
They form as an interesting approach of quantum gravity where discrete geometries
represent quanta of spacetime. The coloring in tensor models improves a lot the topology type of
these discrete structures and this helps a lot in their understanding. In my presentation,
I will review (in a pedestrian way) their construction and then list basic properties of their observables.
Recalling that an observable simply means in this context a convolution or contraction of tensors,
observables of colored tensor models map to bi-partite colored graphs. A first question that one can address
is can we enumerate these observables? I will explain how such an enumeration is possible and
how it has lead us to an intriguing bijection with the counting of branched covers of the 2-sphere.
] 20/09/2016
Eric Hoffbeck Shuffle d'arbresabstract.htmlLes shuffles (battages) jouent un rôle important dans la compréhension du produit d'ensembles simpliciaux, qui intervient à de nombreux endroits en topologie algébrique. Récemment, une généralisation des ensembles simpliciaux a été introduite : les ensembles dendroidaux (on remplace les {0,1,...,p} (avec leur ordre total) par des arbres (avec leur ordre partiel)). La catégorie des ensembles dendroidaux est également munie d'un produit, où interviennent des shuffles d'arbres.
Dans cet exposé, après une brève motivation topologique, j'introduirai cette notion de shuffles d'arbres, en donnant plusieurs définitions équivalentes et de nombreux exemples. Je présenterai ensuite quelques propriétés algébriques et combinatoires de ces shuffles.
Mon exposé est basé sur un travail en commun avec Ieke Moerdijk.
] 06/09/2016
Julien Courtiel Génération des alignements d'arbresabstract.htmlL'alignement d'arbres est la généralisation naturelle de la notion classique d'alignement de séquences. Elle est utilisée dans de nombreux domaines, y compris pour la comparaison de structures secondaires d'ARN (ce qui nous intéressera aujourd'hui). Nous allons donc comprendre comment explorer l'espace des alignements d'arbres et comment déduire des algorithmes efficaces pour comparer les ARN.
Cet exposé introduit ainsi les notions d'alignement de séquences et d'arbres et décrit le problème d'ambiguïté qui point quand nous voulons générer de manière correcte les alignements d'arbres. Pour résoudre ce problème d'ambiguïté dans le contexte des alignements d'arbres, nous donnons un schéma de décomposition sous la forme de grammaire sans contexte. Cela conduit à de nombreux résultats : propriétés statistiques sur les larges structures d'ARN, algorithmes efficaces d'échantillonnage...
Ces travaux, en collaboration avec Cédric Chauve et Yann Ponty, illustrent le fait que la combinatoire peut être un puissant couteau suisse pour traiter des problèmes algorithmiques qui apparaissent dans de nombreux champs appliqués.
] 06/09/2016
Collectif Réunion d'organisation + exposé 26/07/2016
Quoc Hoan Ngo Polylogarithms at non-positive (i.e. negative) multi-indices II [abstract.pdf ] 12/07/2016
Nihar Prakash Gargava Some properties of the image of the star of the plane [abstract.pdf ] 28/06/2016
Quoc Hoan Ngo Polylogarithms at non-positive (i.e. negative) multi-indices [abstract.pdf ] 21/06/2016
Van Chiên Bui Asymptotic expansion of harmonic sums thanks to the Euler-Maclaurin formula and to generating seriesabstract.htmlOn the one hand, asymptotic expansions of harmonic sums are constructed by following the Euler-Maclaurin formula. On the other hand, due to relations among polylogarithms, polyzetas, harmonic sums and their generating series, which are the Lie exponentials in the shuffle and quasi shuffle algebras, we will show structure of polylogarithms and polyzetas. From this, asymptotic expansions of harmonic sums will also establish by following generating series.
] 16/06/2016
Journée MathStic
Rencontre "Combinatoire, Opérades et Probabilités" à Paris 13 14/06/2016
Hoang Ngoc Minh Double regularization of polyzetas at negative multi-indices and polylogarithmic trans-series 07/06/2016
Christophe Tollu Algèbres de Hall (construction catégorique) (2/2) 31/05/2016
Élie de Panafieu Counting connected graphs with large excessabstract.htmlWe enumerate the connected graphs that contain a linear number of edges with respect to the number of vertices. So far, only first term of the asymptotics and a bound on the error were known (Bender Canfield McKay 1995, Pittel Wormald 2005, van der Hofstad Spencer
2006). We present a proof based on analytic combinatorics, i.e. generating function manipulations, and derive the complete asymptotic expansion.
] [article ] 31/05/2016
Hoang Ngoc Minh Transséries polylogarithmiques (2/2) 30/05/2016
Summer School
Transversal Aspects of tilings (30 mai-24 juin)25/05/2016
José Aliste-Prieto Reconstruction of trees and chromatic polynomialabstract.htmlThe U-polynomial of a graph was introduced by Noble and Welsh as a generalization of some invariants coming from Knot theory. It also generalizes the chromatic symmetric function of Stanley. In this talk, we will consider the problem of whether there exist
non-isomorphic trees with the same U-polynomial (or,equivalently, with the same chromatic symmetric function). We will survey what is know about the U-polynomial and this problem. In particular, we will show how to recover some classic invariants from the
U-polynomial and we exhibit several subclasses of trees for which a solution of this problem is known. FInally, we construct some non-isomorphic trees with "almost" the same U-polynomial, based on solutions of an old problem in Number theory due to
Prouhet-Tarry-Escott.
] [article ] 24/05/2016
Peter Nejjar KPZ growth models and Tracy-Widom distributions 24/05/2016
Christophe Tollu Algèbres de Hall (construction catégorique) (1/2) 17/05/2016
Bernhard Gittenberger Analytic combinatorics of lambda-terms 17/05/2016
Hoang Ngoc Minh Transséries polylogarithmiques (1/2) 10/05/2016
Gwendal Collet Limit laws of vertex degree distribution in planar mapsabstract.htmlWe consider the family of rooted planar maps where the vertex degrees belong to a (possibly infinite) set of positive integers.
Using a classical bijection with mobiles and some refined analytic tools to deal with the systems of equations that arise, we first recover the universal asymptotic behaviour of planar maps. Furthermore we establish that the expected number of vertices of a given
degree satisfies a multi-dimensional central limit theorem. We also discuss some possible extension to maps of higher genus.
] 10/05/2016
Gérard Duchamp Abélianisation et majorations de Lappo-Danilevski (4/4) : Propriétés de croisssance [Slides.pdf ]abstract.htmlIn this talk, we start from two sources
[i) The poly- and hyper-logarithms
ii) the classic Dyson series] in order
to develop the theory of noncommutative differential
equations, giving a touch of Lie-theoretic insights
to understand the interplay between orbits and coordinates
which are - following Gelfand's paradigm - special functions.
The talk(s) will be illustrated with concrete examples
and explicit computations.
] 03/05/2016
Collectif
Séance de programme et discussion sur les travaux en cours 03/05/2016
Gérard Duchamp Abélianisation et majorations de Lappo-Danilevski (3/4) : ED bilatères et avec second membre 26/04/2016
Gérard Duchamp Abélianisation et majorations de Lappo-Danilevski (2/4) : ED non-commutatives 19/04/2016
Henri Mühle On Noncrossing partitions for the alternating groupsabstract.htmlThe lattice of noncrossing set partitions of an n -set can be
seen as a subgraph of the Cayley graph of the symmetric group S
generated by all transpositions. We mimic this
construction for the alternating group A2n+1 generated by
all 3-cycles. The resulting poset provides a rich new source of
combinatorics coming from the alternating groups, which in some sense
parallels the combinatorics behind the noncrossing set partitions. We
present some enumerative and bijective results, and suggest an extension
of this construction to all finite Coxeter groups. This is joint work
with Philippe Nadeau.
] 12/04/2016
Alfredo Hubard Métriques extrémales et plongements de graphesabstract.htmlDans cet exposé je présenterai des résultats dans l' intersection de la
géométrie Riemannienne et la topologie algorithmique. Plus précisément, je
discuterai des manières effectives de planariser une surface triangulée, des
problèmes de nombre de croisements, et de la "meilleure" métrique Riemannienne
pour une surface. Si le temps le permet, je parlerai également des défis en
haute dimension et des connections avec les nombres de faces des complexes
simpliciaux.
] 12/04/2016
Valentin Suder Antiderivative functions over F_2^n [Slides.pdf ]abstract.htmlWe use a linear algebra point of view to describe the derivatives and higher order derivatives over F_2^n. On one hand, this new approach ennobles us to prove several properties of these functions, as well as the functions that have these derivatives. On the other hand, we provide a method to construct all of the higher order derivatives in given directions. We also demonstrate some properties of the higher order derivatives and their decomposition as a sum of functions with 0-linear structure. Moreover, we introduce a criterion and an algorithm to realize discrete antidifferentiation of vectorial Boolean functions. This leads us to define a new equivalence of functions, that we call differential equivalence, which links functions that share the same derivatives in directions given by some subspace.
] 12/04/2016
Gérard Duchamp Abélianisation et majorations de Lappo-Danilevski (1/4) : Intégrales itérées 05/04/2016
Sylvain Carrozza O(N) random tensor models [Slides.pdf ]abstract.htmlI will introduce a class of three indices tensor models, endowed with O(N)⊗3 invariance (N being the size of the tensor). They generate weights for general 3-colored graphs, which are not necessarily bipartite. Relying on combinatorial properties of colored graphs,
I will first prove the existence of a 1/N expansion for any such model. I will then focus on a model with two parameters, and illustrate how standard methods from analytic combinatorics allow to compute physical quantities such as critical exponents.
] 30/03/2016
Grégory Miermont Random maps with a boundary: a user's manual 30/03/2016
Benedikt Stufler Limits of random tree-like combinatorial structures 30/03/2016
Vincent Tassion A new proof of the sharpness of the phase transition for Bernoulli percolation on Z^d 30/03/2016
Philippe Marchal Rectangular Young tableaux 29/03/2016
Svetlana Puzynina Infinite self-shuffling wordsabstract.htmlAn infinite word x on an alphabet A is self-shuffling, if x admits factorizations: $x=\prod_{i=1}^\infty U_iV_i=\prod_{i=1}^\infty U_i=\prod_{i=1}^\infty V_i$ with $U_i,V_i \in \A^*$. In other words, there exists a shuffle of x with itself which reproduces x. We prove that many important and well studied words are self-shuffling: This includes the Thue-Morse word and all Sturmian words except Lyndons. We further establish a number of necessary conditions for a word to be self-shuffling, and show that certain other important words (including the paper-folding word and infinite Lyndon words) are not self-shuffling. This new notion has some unexpected applications: As a consequence of our characterization of self-shuffling Sturmian words, we recover a number theoretic result, originally due to Yasutomi, on a classification of pure morphic Sturmian words in the orbit of the characteristic. Finally, we provide a positive answer to a recent question by T. Harju whether square-free self-shuffling words exist and discuss self-shuffling in a shift orbit closure.
] 29/03/2016
Olivier Bouillot Une généralisation des nombres et polynômes de Bernoulli en dimensions supérieures [Slides.pdf ]abstract.htmlLes multizêtas sont des nombres généralisant la fonction zêta de Riemann
au cas de la dimension supérieure. Ces nombres sont (en particulier) définis
sur des n-uplets d'entiers strictement positifs, mais grâce à des prolongements
analytiques, il est possible de les prolonger tous les n-uplets d'entiers.
Cela correspondant alors une généralisation des nombres puis des polynômes
de Bernoulli. Bien qu'il n'y ait pas unicité d'une telle généralisation, nous introduirons un exemple explicite et satisfaisant où nombres de propriétés importantes des polynômes de Bernoulli se transmettent au cas multiple.
Au passage, cela permet de répondre à une question sur la renormalisation
des multizêtas aux entiers négatifs.
] 29/03/2016
Alexander Meduna Regulated Grammars and Automata [Slides.pdf ]abstract.htmlThis talk explains the gist underlying regulated grammars and automata as well as the main purpose of their investigation. This investigation is classified into four major topics--the study of their power, properties, reduction, and mutual convertibility. The talk illustrates this inevstigation by a case study in terms of one-sided random-context grammars. Most importantly, it points out that propagating versions of one-sided random-context grammars characterize the family of context-sensitive languages, and with erasing rules, they characterize the family of recursively enumerable languages; as a result, they are stronger than ordinary random context grammars. Open problem areas are formulated.
] 22/03/2016
Colloque en l'honneur de Marcel-Paul Schützenberger (21-25 mars, Bordeaux)22/03/2016
Axel Bacher Lattice paths in 3D 22/03/2016
Martin Delacourt Calculer dans un automate cellulaire unidirectionnel réversible : vers l'indécidabilité de la périodicité?abstract.htmlOn s'intéresse au parallèle entre 2 problèmes sur des modèles
distincts d'automates. D'une part, les automates de Mealy
(transducteurs lettre à lettre complets) qui produisent des
semi-groupes engendrés par les transformations sur les mots infinis
associées aux états. En 2013, Gillibert a montré que le problème de la
finitude de ces semi-groupes était indécidable. En revanche la
question est ouverte dans le cas où l'automate de Mealy produit un groupe.
D'autre part, les automates cellulaires unidirectionnels pour
lesquels la question de la décidabilité de la périodicité est ouverte.
On peut montrer l'équivalence de ces problèmes.
On fera un pas dans cette étude en montrant qu'il est possible de
simuler du calcul Turing dans un automate cellulaire unidirectionnel
réversible, rendant ainsi des problèmes de prédiction indécidables
ainsi que la question de la périodicité partant d'une configuration finie.
] 15/03/2016
Mathias Pétréolle Partitions d'entiers et groupes de Coxeter [Slides.pdf ]abstract.htmlEn 2009, Han a redécouvert et généralisé une identité due à Nekrasov
et Okounkov, qui fait un lien entre d'un coté, les puissances de la
fonction êta de Dedekind, et de l'autre les partages d'entiers et leurs
longueurs d'équerres. Pour cela, il utilise la formule de Macdonald pour
le système affine de racines de type A. Je montrerai comment, à l'aide
de bijections, il est possible de démontrer des identités de
Nekrasov-Okounkov pour d'autres types de systèmes de racines (type
affine C et D notamment), et je présenterai les nouvelles formules des
équerres qui en découlent.
Dans une seconde partie, je présenterai la notion d'éléments
cycliquement pleinement commutatifs dans les groupes de Coxeter, qui ont
été introduits pour étudier une version cyclique d'un théorème de
Matsumoto. Je montrerai ensuit comment, en utilisant la théorie des
automates finis, on peut démontrer que la série génératrice de ces
éléments est une fraction rationnelle, quelque soit le groupe de Coxeter
considéré.
] 15/03/2016
Bérénice Delcroix-Oger Algèbre de Hopf d'incidence des posets de partitions semi-pointées [Slides.pdf ]abstract.htmlDans les années 1990, Schmitt a décrit un procédé qui permet d'associer à toute famille d'intervalles vérifiant certaines conditions une algèbre de Hopf, appelée algèbre de Hopf d'incidence. Une algèbre de Hopf d'incidence bien connue est celle associée aux posets
de partitions, aussi connue sous le nom d'algèbre de Hopf de Faà Di Bruno.
Après avoir rappelé les définitions nécessaires et présenté l'algèbre de Faà di Bruno, nous introduirons une algèbre de Hopf généralisant celle de Faà di Bruno : l'algèbre de Hopf d'incidence des partitions semi-pointées.
[En fonction du temps qui me restera, j'évoquerai mes récents résultats en collaboration avec J.-C. Aval, Adrien Boussicault, P. Laborde-Zubieta et F. Hivert sur les arbres non ambigus. ]
] 08/03/2016
Journées Aléa (7-11 mars 2016)08/03/2016
Gérard Duchamp Non-commutative diffferential equations and (some) infinite dimensional Lie groups 01/03/2016
Grégory Châtel Algèbre de Hopf cambrienneabstract.htmlEn 1998, Loday et Ronco décrivent une algèbre de Hopf combinatoire dont la base est indicée par des arbres binaires. Cette algèbre possède de nombreux liens avec divers résultats antérieurs. Son produit est en particulier lié aux intervalles du treillis de Tamari, structure d'ordre partiel dont les éléments sont des arbres binaires. En 2006, Reading définit la notion de treillis cambrien d'un groupes de Coxeter. Le treillis Cambrien généralise l'ordre de Tamari en utilisant des structures arborescentes qui généralisent les arbres binaires : les arbres cambriens. Une question naturelle se pose alors : est-il possible de généraliser l'algèbre de Hopf de Loday-Ronco aux arbres cambriens ? Dans cette présentation, j'expliquerai les résultats que nous avons obtenus avec Vincent Pilaud sur les arbres cambriens en type A.
] 23/02/2016
Aléa in Europe (22-26 février, München)17/02/2016
STACS'2016 (17-20 février)16/02/2016
Benjamin Hellouin Uniformisation de l'aléa en dynamique symboliqueabstract.htmlUne transformation T : X -> X d'un espace X est dite randomisante si son itération tend à uniformiser la distribution des configurations de l'espace X. Plus précisément, quand une mesure de probabilité initiale non uniforme est fixée sur X (la distribution
initiale), l'itération de la transformation T fait converger cette mesure vers la mesure uniforme.
] 16/02/2016
Christophe Tollu Algèbres de (Ringel-)Hall (2/2)abstract.htmlDans l’espoir de comprendre certains travaux récents de Berenstein et Rudel (« Quantum cluster characters of Hall algebras », arXiv:1308.2992 et « The Feigin tetrahedron », arXiv:1401.4338v2), en particulier la construction d’un homomorphisme, appelé « quantum shuffle character », entre le dual de l’algèbre de Ringel-Hall et l’algèbre de mélange quantique, j’étudierai l’algèbre de Ringel-Hall, en insistant sur sa structure d’algèbre de Hopf auto-duale.
] 12/02/2016
Damien Pous Hacking nondeterminism with induction and coinductionabstract.htmlFinite automata are used in a wide range of verification problems. We introduce "bisimulation up to congruence" as a technique for proving language equivalence of non-deterministic finite automata. Exploiting this technique, we devise an optimisation of the classical algorithm by Hopcroft and Karp which, as we show, is exploiting a weaker "bisimulation up to equivalence" technique. The resulting algorithm can be exponentially faster than the recently introduced "antichain algorithms".
] 09/02/2016
Nicolas Basset Mesure des langages temporisés et applications à la combinatoire des permutationsabstract.htmlDans un premier temps j'exposerai de manière générales la théorie de la volumétrie
des langages temporisés développés durant (et depuis) ma thèse.
Avec mes collègues nous avons trouvé des applications à cette théorie
dans divers domaines de recherche tels que
la théorie de l’information, la vérification,
la combinatoire énumérative.
Dans un second temps, je décrirai plus précisément comment étant donné un automate temporisé,
on peut exprimer et calculer son entropie et sa fonction génératrice des volume s
à l'aide de la théorie spectrale d'un opérateur fonctionnel associé à cet automate temporisé.
Nous fonctionnons par analogie avec le cas discret, au lieu d'appliquer la théorie de Perron-Frobenius à la matrice d'adjacence d'un automate fini,
nous appliquons la théorie des opérateurs positifs agissant sur les espaces de Banach à l'opérateur fonctionnel de notre automate temporisé.
Dans un troisième temps je décrirai les applications au dénombrement et à la génération aléatoire de permutations dans les classes régulières
(c'est à dire chaque permutation de la classe a un mot de montées et de descentes appartennant à un langage régulier donné).
Nous nous intéresserons particulièrement à la génération aléatoire par générateur de Boltzmann et par processus stochastique d'entropie maximal.
] 02/02/2016
Anne Bouillard Une formule de Möbius pour les groupe de tracesabstract.htmlLes groupes de traces sont une généralisation des monoïdes de
traces (encore appelés monoïdes partiellement commutatifs libres). Un
résultat de 1969 de Carier et Foata montre l'existence d'une formule
d'inversion de Möbius pour la série génératrice du monoïde de traces.
Nous généralisons ce résultat aux groupes de traces, ce qui nous
permettra également d'étudier la hauteur moyennes des traces.
] 02/02/2016
Gérard Duchamp Exponentielles dans l'algèbre de shuffle et transcendence 27/01/2016
Journées combinatoires de Bordeaux (27-29 janvier)26/01/2016
Inhomogeneous Random Systems et Journées de physique statistique @ ENS (26-29 janvier)21/01/2016
Camille Coti Exploiting Redundant Computation in Communication-Avoiding Algorithms for Algorithm-Based Fault Tolerance 21/01/2016
Bilel Sdiri Contrast enhancement method for stereo endoscopic images based on binocular just noticeable difference model 21/01/2016
Caio Filippo Corro Méthode lagrangienne pour les arborescences couvrantes avec application en traitement automatique des langues 21/01/2016
Lionel Pournin L'opération de flip dans les triangulations : du stockage de données à la topologie des surfaces 21/01/2016
Bénédicte Haas The CRT is the scaling limit of large random dissections 21/01/2016
Journée MathStic 19/01/2016
Journées du GDR-IM (18-20 janvier)13/01/2016
Julien Courtiel Cordes terminales dans les diagrammes connexes de cordesabstract.htmlPeut-être souvent mésestimés, les diagrammes de cordes et leur énumération apparaissent dans de nombreux domaines mathématiques : physique quantique, théorie des noeux, échantillonnage de graphes, analyse de structures informatiques, et même bio-informatique...
Les travaux de cet exposé, en cours de rédaction et coréalisés avec Karen Yeats (SFU, Vancouver), se placent de le cadre de la physique quantique. En effet, les solutions à certaines équations de Dyson-Schwinger (nous n'en parlerons que très peu, soyez rassurés) peuvent être définies grâce aux diagrammes de cordes connexes munies d'un paramètre particulier : les cordes dites terminales.
Nous étudierons donc quelques statistiques sur ces cordes terminales : leur nombre en moyenne, la position de la première corde terminale, etc. Nous constaterons notamment l'apparition d'une loi limite de probabilité qui, à ma connaissance, n'est pas répertoriée dans la littérature. Nous montrerons également en quoi les techniques classiques de combinatoire analytique ne peuvent s'appliquer et donnerons quelques idées sur la démarche à emprunter dans ce cas-là.
] 12/01/2016
Gérard Duchamp Exponentielles dans l'algèbre de shuffle et transcendence 05/01/2016
CALIN
Réunion d'équipe 05/01/2016
Gabriel Renault Jeux dead-ending en version misèreabstract.htmlLes jeux combinatoires sont des jeux finis sans hasard à deux joueurs et à information complète. En convention normale, un joueur perd lorsqu'il ne peut plus jouer, alors que ce joueur gagnerait en convention misère. La théorie des jeux combinatoires développée par Berlekamp, Conway et Guy pour les jeux en convention normale a donné peu de résultats pour les jeux en convention misère, ce qui explique que nous étudiions ici un sous-ensemble de jeux, appelés dead-ending, dans lesquels un joueur qui ne peut pas jouer à un certain point ne pourra plus jamais jouer dans ce jeu, quelle que soit la séquence de coups jouée par son adversaire. Les jeux combinatoires peuvent être représentés par des arbres dans lesquels les fils d'un nœud représentent les positions que les joueurs peuvent atteindre depuis la position que le nœud représente. Nous étudions la somme des jeux dead-ending et utilisons ses propriétés pour réduire ses arbres, leur donnant une forme canonique et garantissant que l'inverse d'un jeu inversible est naturel.
] 05/01/2016
Collectif
Bonne année + opérateurs intégraux dans le plan doublement fendu 15/12/2015
Andrea Sportiello Sur la forme limite de l'identité dans le tas de sable abélienabstract.htmlLe modèle du tas de sable abélien décrit d'une façon élémentaire des processus de diffusion dans des réseaux. Des configurations de sable instables se stabilisent en des configurations stables, suite à une dynamique de avalanches. Malgré sa simplicité, ce modèle
présente des phenoménes surprenants. On peut ansi considérer des configurations instables très simples à décrire, sur des réseaux réguliers, et observer le résultat à la fin de l'avalanche : on verra apparaitre des formes fractales complexes.
Une de ces configurations est l'identité récurrente, Id. Quand le graphe est une portion carrée, de taille L, du réseau carré. On a donc une suite Id(L) de configurations, qui, mises à l'échelle, semblent converger vers une forme limite fractale qui fascine les
chercheurs depuis longtemps.
On vient d'obtenir une description complète de cette forme. Ce résultat fait apparaitre plusieurs surprises : tous les points de contact entre les morceaux qui forment la fractale ont des coordonnées (x,y) qui appartiennent au meme corps cubique. Par exemple, le bien
connu "carré bleu" qu'on trouve au milieu de la configuration est à une distance du bord de 0.58315637..., c'est-à-dire, la seule racine réelle de l'équation 2x^3+3x^2+x-2=0.
] 15/12/2015
Philippe Biane Gog, Magog et Schützenberger 15/12/2015
Bénédicte Haas Le CRT est la limite d'échelle de grandes dissections aléatoiresabstract.htmlUne dissection du polygone régulier à n côtés est la graphe formé par le polygone et certaines de ses diagonales, avec la règle que deux diagonales ne peuvent se croiser qu'aux sommets du polygone. On s'intéresse ici au comportement asymptotiquement d'une dissection
uniformément distribuée dans l'ensemble des dissections du polygone à n côtés. Nous verrons que multipliée par n^(-1/2) cette dissection uniforme converge vers un multiple du CRT brownien. Ce résultat se généralise à des mesures attribuant des poids de Boltzmann aux
degrés des faces des dissections, lorsque ces poids décroissent suffisamment vite.
Il s'agit d'un travail en collaboration avec Nicolas Curien et Igor Kortchemski.
] 15/12/2015
Bodo Lass Polynômes symétriques et inégalitésabstract.htmlUn théorème fondamental pour la théorie des égalités affirme que les polynômes symétriques élémentaires engendrent la sous-algèbre des polynômes symétriques, et sont algébriquement indépendants. Nous explorons l'utilité de ce résultat pour la théorie des inégalités.
] 15/12/2015
Tanguy Rivoal Approximants de Padé et polyzêtasabstract.htmlPeu de résultats sont connus sur la nature diophantienne des valeurs de la fonction zêta et de leurs généralisations, les polyzêtas. Une méthode générale pour parvenir à montrer l'irrationalité de tel ou tel nombre consiste à construire des approximations
polynomiales, dites de Padé, de séries entières, puis à spécialiser pour obtenir des approximations numériques de ces nombres. Je présenterai diverses constructions d'approximants de Padé dans le contexte des polyzêtas. Certaines proviennent de travaux en commun
avec Stéphane Fischler.
] 15/12/2015
Christian Krattenthaler Un théorème de factorisation pour le nombre des pavages en losanges d'un hexagone avec des trous triangulairesabstract.htmlJe présenterai un curieux théorème de factorisation pour le nombre des pavages en losanges d'un hexagone avec
symétrie verticale et horizontale dont plusieurs trous
triangulaires ont été enlevés le long de l'axe de symétrie horizontale. Je relierai ce théorème avec des autres
théorèmes de factorisation, et je discuterai quelques conséquences et questions ouvertes.
Ce travail a été effectué en commun avec Mihai Ciucu.
"A factorisation theorem for the number of rhombus tilings of a hexagon with trianglar holes"
I shall present a curious factorisation theorem for the number of rhombus tilings of a hexagon with vertical and
horizontal symmetry axis, with triangular holes along the latter axis. I shall set this theorem in relation with
other factorisation theorems, and discuss some consequences and open questions.
This is joint work with Mihai Ciucu.
] 15/12/2015
Journée en l'honneur de Christian Krattenthaler 14/12/2015
Remise du doctorat honoris causa à Christian Krattenthaler 08/12/2015
Luca Lionni Colored triangulations of arbitrary dimensions are stuffed Walsh mapsabstract.htmlRegular D-edge-colored graphs encode D-dimensional colored triangulations of
pseudo-manifolds. We study such families of edge-colored graphs built from a
finite but arbitrary set of building blocks, which extend the notion of
p-angulations to arbitrary dimensions. I will introduce a bijection between any
such family and some colored combinatorial maps which we call stuffed Walsh
maps. Those maps generalize Walsh's representation of hypermaps as bipartite
maps, by replacing the vertices which correspond to hyperedges with
non-properly-edge-colored maps.
We are interested in the number of bi-chromatic cycles of the initial
edge-colored graphs because because they encode the curvature of the
corresponding triangulated pseudo-manifold. I will therefore present new tools
that use the bijection in order to study the graphs which maximize the number
of bi-chromatic cycles at fixed number of vertices and provide examples where
the corresponding stuffed Walsh maps can be completely characterized.
] [article ] 08/12/2015
Christophe Tollu Algèbres de (Ringel-)Hall (1/2). Suivi de : Échelles de comparaison abstract.htmlAlgèbres de (Ringel-)Hall Suivi de : Échelles de comparaison et développements singuliers.
Dans l’espoir de comprendre certains travaux récents de Berenstein et Rudel (« Quantum cluster characters of Hall algebras », arXiv:1308.2992 et « The Feigin tetrahedron », arXiv:1401.4338v2), en particulier la construction d’un homomorphisme, appelé « quantum shuffle character », entre le dual de l’algèbre de Ringel-Hall et l’algèbre de mélange quantique, j’étudierai l’algèbre de Ringel-Hall, en insistant sur sa structure d’algèbre de Hopf auto-duale.
En deuxième partie est prévu un rapppel de ce que sont les échelles suivant des bases de filtres générales (voisinages, pointés, fendus, bases de filtre de Fréchet,
complémentaires de points isolés etc...). On appliquera ces notions aux développements singuliers de P. Flajolet et A. Odlyzko. Une discussion générale sur les travaux en cours s'ensuivra.
] 03/12/2015
Séminaire Flajolet Timothy Budd, Jehanne Dousse, Yann Bugeaud 03/12/2015
Yinon Spinka Long-range order in random 3-colorings of Z^dabstract.htmlConsider a random coloring of a bounded domain in Zd with the probability of each coloring F proportional to exp(-β*N(F)), where β>0 is a parameter (representing the inverse temperature) and N(F) is the number of nea rest neighboring pairs colored by the same color. This is the anti-ferromagnetic 3-state Potts model of statistical physics, used to describe magnetic interactions in a spin system. The Kotecký conjecture is that in such a model, for d≥3 and high enough β, a sampled coloring will typically exhibit long-range order, placing the same color at most of either the even or odd vertices of the domain. We give the first rigorous proof of this fact for large d. This extends previous works of Peled and of Galvin, Kahn, Randall and Sorkin, who treated the case β=infinity.
No background in statistical physics will be assumed and all terms will be explained thoroughly.
Joint work with Ohad Feldheim.
] 02/12/2015
Mark Ward An overview of an analytic approach for branching processes (Colloquium : Les mercredis du LIPN)abstract.html One approach to solving some questions in probability theory--especially questions about asymptotic properties of algorithms and
data structures--is to take an analytic approach, i.e., to utilize
complex-valued methods of attack. These methods are especially useful with
several types of branching processes, leader election algorithms, pattern
matching in trees, data compression, etc. This talk will focus on some of
the highlights of this approach. I endeavor to keep it at a level that is
accessible for graduate students.
] 02/12/2015
Yinon Spinka Random 3-colorings of Z^dabstract.htmlLattice spin systems are used in statistical physics to model various magnetic materials.
I will first introduce some well-known models in this field and give a short review of known results,
with an emphasis on the phenomenon of long-range order.
I will then discuss a result on the existence of long-range order for random 3-coloring of Z^d in high-dimensions (joint work with Ohad Feldheim).
Finally, I will also discuss a result of long-range order for the loop O(n) model on the hexagonal lattice (joint work with Hugo Duminil-Copin, Ron Peled and Wojciech Samotij).
No background in statistical physics will be assumed and all terms will be explained thoroughly.
] 01/12/2015
Yinon Spinka Long-range order in lattice spin systemsabstract.htmlLattice spin systems are used in statistical physics to model various magnetic materials.
I will first introduce some well-known models in this field and give a short review of known results,
with an emphasis on the phenomenon of long-range order.
I will then discuss a result on the existence of long-range order for random 3-coloring of Z^d in high-dimensions (joint work with Ohad Feldheim).
Finally, I will also discuss a result of long-range order for the loop O(n) model on the hexagonal lattice (joint work with Hugo Duminil-Copin, Ron Peled and Wojciech Samotij).
No background in statistical physics will be assumed and all terms will be explained thoroughly.
] 24/11/2015
semaine de physique combinatoire @IHP (60 ans d'Alan Sokal et de Vincent Rivasseau ) 18/11/2015
Hsien-Kuei Hwang Coin Tossing in algorithmics (Colloquium : Les mercredis du LIPN)abstract.htmlCoin-tossing is one of the simplest ways of resolving a conflict, deciding between two alternatives, and generating random phenomena. It has been widely adopted in many daily-life situations and scientific disciplines. In this talk, I will present a few research themes connected to the use of coin-tossing in algorithmics, taken from my research: these include random permutations, data structures, evolutionary algorithms and leader selection. The main focus will be on the stochastic behaviors and the methods of analysis.
] 17/11/2015
Frédéric Chyzak A computer-algebra-based formal proof of the irrationality of zeta(3) [Slides.pdf ]abstract.htmlWe report on the formal verification of an irrationality proof of the evaluation at 3 of the Riemann zeta function. This verification uses
the Coq proof assistant in conjunction with algorithmic calculations in Maple. This irrationality result was first proved by Apéry in
1978, and our formalization follows the proof path of his original presentation. The crux of it is to establish that some sequences
satisfy a common recurrence. We formally prove this by an a posteriori verification of calculations performed by a Maple
session. This bases on computer-algebra algorithms implementing Zeilberger's approach of creative telescoping. This experience
illustrates the limits of the belief that creative telescoping can discover recurrences for holonomic sequences that are easily checked a
posteriori. We discuss this observation and describe the protocol we devised in order to produce complete formal proofs of the recurrences.
Beside establishing the recurrences, our proof combines the formalization of arithmetical ingredients and of some asymptotic analysis.
] 10/11/2015
Yining Hu The Flajolet-Soria formula, Furstenberg and Christol's theoremsabstract.htmlPart 1: We show that the Flajolet-Soria coeffcient extraction formula for algebraic series can be deduced from a theorem of Furstenberg, with which we can prove that the formula is valid for all fields and not only for the complex field.
] 03/11/2015
Thomas Wong Enumeration problems in directed walk modelsabstract.htmlSelf-avoiding walks appear ubiquitously in the study of linear polymers as it
naturally captures their volume exclusion property. However, self-avoiding
walks are very difficult to analyse with few rigourous results available.
In 2008, Alvarez et al. determined numerical results for the forces induced by
a self-avoiding walk in an interactive slit. These results resembled the exact
results for a directed model in the same setting by Brak et al. in 2005,
suggesting the physical consistency of directed walks as polymer models.
Via the kernel method, we extend the directed walk model to a series of models
involving two directed walks as a way to find exact enumerative results for
studying the behaviour of ring polymers near an interactive wall, or walls. In
the final model we considered, we are unable to find exact solutions via the
kernel method. Instead, we use transfer matrices to obtain numerical results
that are qualitatively similar to those presented by Alvarez et al.
] 27/10/2015
Thomas Fernique Degré algébrique des pavagesabstract.htmlOn s'intéresse aux pavages par carrés et losanges qui discrétisent des plans de
l'espace à quatre dimensions. Plus précisément, on veut savoir lesquels peuvent
être caractérisés par leurs motifs locaux. Il se trouve qu'ils correspondent à
des plans définis par des entiers quadratiques (et pas plus). La généralisation
aux pavages par plus de losanges reste ouverte.
] 27/10/2015
Quoc Hoan Ngo The combinatorics of harmonic sums and polylogarithms at negative integer multi-indices [abstract.pdf ] 20/10/2015
Philippe Marchal Forme limite de tableaux de Young rectangulairesabstract.htmlEn 2004, Pittel et Romik ont montré l'existence d'une forme limite
pour les tableaux de Young rectangulaires.
Je montrerai comment la méthode probabiliste des "densités", que je développe depuis quelques travaux déjà,
permet de retrouver cette forme limite et donne aussi les fluctuations sur le
bord : on trouve une gaussienne dans les coins et Tracy-Widom ailleurs sur le bord.
] 13/10/2015
Olivier Bodini Analyse asymptotique et génération aléatoire des structures en diamantabstract.htmlNous allons d'écrire et étudier une classe importante de DAG, appelé structure en diamant. Cette étude repose sur une analyse asymptotique d'équations différentielles non linéaires. Nous expliquerons aussi comment développer des générateurs aléatoires efficaces pour
ces structures. Travail en commun avec
Hsien-Kuei Hwang, Antoine Genetrini et Xavier Fontaine.
] 13/10/2015
Gérard Duchamp Théorème de Wei-Norman (2/2) 09/10/2015
Stéphane Dartois Tenseurs aléatoires (soutenance de thèse)abstract.htmlDuring this defense I present pieces of the work I achieved on random tensor models (tensor models for short). I will define colored triangulations and then review their combinatorics. After this is done I show how one can write integral representation of their generating series. These representations are called tensor models. Using this representation I will describe the combinatorial 1/N expansion for two different kinds of models generating specific classes of colored and non-colored combinatorial maps. I will then concentrate on a specific model, that is the simpler non trivial tensor model and explore some of its properties. In particula r I review the properties of its double scaling limit, then using its Hubbard-Stratanovitch representation, I show how one can use matrix models techniques to recover results obtained using combinatorial techniques. I will finally present several results that point towards integrable structures in the framework of random tensor models.
] 06/10/2015
Pascal Vanier Calculabilité et pavages [Slides.pdf ]abstract.html Les pavages, ou sous-shifts de type fini sont des ensembles de coloriages du plan vérifiant des contraintes locales en nombre fini.
Nous nous intéresserons en particulier au problèmes d'isomorphisme entre sous-shifts, connu sous le nom de conjugaison et plus
particulièrement aux invariants de conjugaison, qui sont des "objets" permettant de caractériser certains aspects des sous-shifts.
Nous donnerons en particulier des caractérisations calculatoires de ces derniers qui permettront de voir les liens intimes qui lient
pavages et classes de complexité/calculabilité.
] 06/10/2015
Hoang Ngoc Minh Théorème de Wei-Norman (1/2) 29/09/2015
pôle MathStic Réunion axe 3 (Physique mathématique, physique statistique, combinatoire) 29/09/2015
Van Chiên Bui Harmonic sums computed at transcendence bases 23/09/2015
Sergio Caracciolo A fresh view on the matching problemabstract.htmlI will review some new results in the stochastic euclidean bipartite
matching problem.
First I will look at the simple one dimensional version, for which
many exact results can be achieved. Afterwards, by discarding the
discrete nature of the problem, as usual in a critical system, I will
show how it is possible to resort to a continuous version for which an
analytical expression for the minimum cost and correlation functions
can be computed.
] 22/09/2015
pôle MathStic Réunion (12h30-14h30) axe 1 (Optimisation et apprentissage appliqués aux contenus numériques) 22/09/2015
Journées du GT Combinatoire Algébrique du GDR IM 15/09/2015
Gérard Duchamp About the "new" Bourbaki (2012) 08/09/2015
Michael Wallner Why and when does the half-normal distribution appear in combinatorics?abstract.htmlWe present an extension of a theorem by Michael Drmota and Michèle Soria [1997] that can be used to identify the limiting distribution for a class of combinatorial schemata. This is achieved by determining analytical and algebraic properties of the associated
bivariate generating function.
We give sufficient conditions implying a half-normal limiting distribution, extending the known conditions leading to either a Rayleigh, a Gaussian or a convolution of the last two distributions. Finally, we present some applications to lattice path and tree enumeration, images and preimages in random mappings.
] 07/07/2015
Joshua Socolar Nonlinear dynamics and complex systems 30/06/2015
Gérard Duchamp Autour de la question : Local coordinates on (infinite dimensional) Lie groups, factorization of Riemann zeta functions 24/06/2015
Kilian Raschel Walks in the quarter plane with arbitrary big jumps 24/06/2015
Marni Mishna Uniform random generation of walks in the quarter-plane 24/06/2015
buffet combinatorico-probabiliste 24/06/2015
Grégory Schehr Statistics of the real roots of real random polynomials 24/06/2015
Anne-Laure Basdevant Dénombrement de plus longues sous-suites croissantes 24/06/2015
Journée MathStic
Combinatoire et probabilités 23/06/2015
Hoang Ngoc Minh Adjunction and combinatorics of duality 16/06/2015
Aladin Virmaux Représentations de tours de monoïdes et algèbres de Hopfabstract.htmlLes monoïdes J-triviaux forment une importante famille de monoïdes dont
l'étude
des représentations est particulièrement combinatoire. De plus, certains
exemples (la paire NCSF/Qsym est catégorifiée par les monoïdes 0-Hecke,
l'algèbre de Weyl par NilHecke, etc) laissent suggérer que ce sont des
candidats naturels pour catégorifier certaines algèbres de Hopf.
Dans cet exposé, nous considérerons des tours de monoïdes J-triviaux et
étudierons des formules générales d'induction et de restriction. Nous
verrons en
détail le cas des tours de semi-treillis duquel on tire des
"semi-catégorifications" de
certaines algèbres de Hopf (FQSym, PBT, NCSF).
] [article ] 09/06/2015
Van Chiên Bui Two q -deformations of multiple polylogarihms 02/06/2015
Katarzyna Górska Explicit forms and combinatorial content of Levy stable distributions [abstract.pdf ] 02/06/2015
Quoc Hoan Ngo Multiple- polylogarithms at non-positive integers and Rota-Baxter operators [abstract.pdf ] 26/05/2015
Louis Dumont Efficient Algebraic Diagonals and Walks [Slides.pdf ]abstract.htmlThe diagonal of a multivariate power series F is the univariate power series Diag F generated by the diagonal terms of F. Diagonals form an important class of power series; they occur frequently in number theory, theoretical physics and enumerative combinatorics. We
study algorithmic questions related to diagonals in the case where F is the Taylor expansion of a bivariate rational function. It is classical that in this case Diag F is an algebraic function. We propose an algorithm that computes an annihilating polynomial for
Diag F. Generically, it is its minimal polynomial and is obtained in time quasi-linear in its size. We show that this minimal polynomial has an exponential size with respect to the degree of the input rational function. Throughout the talk, we use a common problem
of counting certain lattice walks to illustrate the capacities and limits of our tools.
] 26/05/2015
Katarzyna Górska Photoluminescence decay of silicon nanocrystals and Lévy stable distributions [abstract.pdf ] 21/05/2015
Dmytro Volin Quantum spectral curve and multiple zeta values (2/2) [Slides.pdf ]abstract.htmlThe AdS/CFT (anti-de Sitter/conformal field theory) quantum spectral curve is a tool for computing the conformal
spectrum of a four-dimensional gauge theory, N=4 SYM, in the planar limit.
This tool proved to be very efficient: we were able to get the explicit
10-loop perturbative results. The answer is expressed in terms of multiple
zeta values. I will explain what the quantum spectral curve is and how the
multiple zeta values emerge from it.
] 21/05/2015
Dmytro Volin Quantum spectral curve and multiple zeta values (1/2) [Slides.pdf ]abstract.htmlThe AdS/CFT (anti-de Sitter/conformal field theory) quantum spectral curve is a tool for computing the conformal
spectrum of a four-dimensional gauge theory, N=4 SYM, in the planar limit.
This tool proved to be very efficient: we were able to get the explicit
10-loop perturbative results. The answer is expressed in terms of multiple
zeta values. I will explain what the quantum spectral curve is and how the
multiple zeta values emerge from it.
] [article ] 20/05/2015
Journées LAGA surfaces plates (J.C. Yoccoz , A. Zorich , G. Forni )12/05/2015
Jean-Baptiste Priez Énumération d'automates minimaux et fonctions de parking [Slides.pdf ]abstract.htmlLes fonctions de parking sont intéressantes pour de nombreuses raisons.
Elles sont en bijection avec les séquences de Prüfer, les chemins de Dyck
décorés, etc., et sont liées à l’inversion de Lagrange, aux polynômes
harmoniques diagonaux, etc.
En particulier, elles sont en bijection
avec les forêts d'arbres enracinés, autrement dit avec les endo-fonctions
acycliques.
En 2002, Jim Pitman et Richard P. Stanley ont introduit une généralisation
des fonctions de parking. Nous verrons qu'une sous-famille de ces fonctions
de parking généralisées est en bijection avec l’ensemble des fonctions de
transition des automates finis déterministes acycliques. Nous expliciterons
une bijection et nous montrerons que cette dernière transporte une
information précieuse sur les langages droits des états de l'automate.
Nous utiliserons cette information pour extraire et énumérer les automates
acycliques non-initiaux pour lesquels tous les langages droits des états
sont distincts. Enfin, par une technique usuelle de graphes, nous
obtiendrons une formule exacte d'énumération des automates acycliques
minimaux.
] [article ] 12/05/2015
Mikhael Berlinkov Various aspects of automaton synchronization [Slides.pdf ] [abstract.pdf ] 07/05/2015
Alexandra Ugolnikova Soutenance à mi parcours : Tilings 07/05/2015
Quentin de Mourgues Soutenance à mi-parcours : A left/right dynamic on permutationsabstract.htmlSoit s une permutation dans Sigma_n.
Soit i(s)=s(1), j(s)=s^{-1}(1),
Soit C_k le cycle 1>2>...>(k-1)>1 (k,k+1,..,n points fixes).
On definit L et R comme suit:
L(s) = C_{j(s)}.s
et
R(s) = s.C_{i(s)}^{-1}
Il est facile de voir que L et R sont inversibles, la dynamique L/R partitionne donc Sigma_n en classes d'équivalence qui sont des graphes orientés
uniformes (une arête entrant/sortant par "couleur" L et R) fortement connexes.
Dans cet exposé, on étudiera ces classes : leur nombre, leur taille, leur structure, etc.
] 05/05/2015
Samuel Lelièvre Comptage et énumération de surfaces plates, formes quasimodulaires [Slides.pdf ] 21/04/2015
Thierry Bousch La tour de Hanoï, revue par Dudeney [Slides.pdf ]abstract.htmlDans la version classique de "la Tour de Hanoï", c'est-à-dire
avec trois aiguilles, on sait bien qu'on peut transférer N disques
d'une aiguille vers une autre en 2^N-1 mouvements, et que ce nombre
est minimal. Ajoutons une quatrième aiguille: quel est alors le nombre
minimum de mouvements nécessaires pour transférer N disques d'une
aiguille vers une autre? Etrangement, ce problème posé il y a plus
d'un siècle par le puzzliste anglais Henry Ernest Dudeney n'a été
résolu que tout récemment. Et pour d'autres variantes de la Tour
de Hanoï, avec davantage d'aiguilles ou des restrictions sur les
mouvements, le problème est largement ouvert.
http://www.cnrs.fr/insmi/spip.php?article1170
] 14/04/2015
Thibault Manneville Diamètre et hamiltonicité des associaèdres de graphe [Slides.pdf ] 14/04/2015
Gérard Duchamp Motzkin paths and phi-shuffle 07/04/2015
Loï Foissy Structure algébrique des opérateurs de Fliess [Slides.pdf ] [article ] [article ] 07/04/2015
Quoc Hoan Ngo Soutenance de thèse à mi-parcours 07/04/2015
Van Chiên Bui Soutenance de thèse à mi-parcours 31/03/2015
Erik Aas Multi-type TASEP on a ringabstract.htmlI will give an introduction to, and describe recent research on the
multi-type TASEP on a ring. This is a Markov process on permutations
given by randomly sorting (cyclically) adjacent letters in the
permutation at hand. The model is motivated both by physical and
combinatorial considerations. The stationary distribution has a nice
description in terms of the multi-line queues discovered by Ferrari
and Martin.
] [article ] 31/03/2015
Gérard Duchamp Intégrales itérées et (indépendance linéaire des) fonctions coordonnées 24/03/2015
Gwendal Collet Automates d'arbres [Slides.pdf ] 17/03/2015
Journées Aléa Aléa, au CIRM (16-20 mars) 17/03/2015
Gérard Duchamp Phi-shuffle and various combinatorial Hopf algebras (2/2): Hunting the antipode of infiltration products (discussion) 17/03/2015
Gérard Duchamp Phi-shuffle and various combinatorial Hopf algebras (1/2): Infiltration and evaluation of Motzkin Paths (discussion) 11/03/2015
André Katz Une histoire personnelle des pavages et quasi-cristaux [abstract.pdf ] 11/03/2015
Cédric Boutillier Le modèle d'Ising XOR : une interprétation par les dimères bipartis [Slides.pdf ] 11/03/2015
Béatrice de Tilière Le laplacien massique Z-invariant sur les graphes isoradiaux [Slides.pdf ] 10/03/2015
Sébastien Labbé Une généralisation des mots de Christoffel en dimension d [Slides.pdf ]abstract.htmlIn this work, we extend the definition of Christoffel words to
directed subgraphs of the hypercubic lattice in arbitrary dimension
that we
call Christoffel graphs. Christoffel graphs when d=2 correspond to
well-known Christoffel words.
We show that Christoffel graphs have similar properties to those of
Christoffel words: symmetry of their central part and conjugation with
their
reversal. Our main result extends Pirillo's theorem (characterization of
Christoffel words which asserts that a word amb is a Christoffel
word if and only if it is conjugate to bma) in arbitrary dimension.
In the generalization, the map amb\mapsto bma is seen as a flip
operation on
graphs embedded in Z^d and the conjugation is a translation.
We show that a fully periodic subgraph of the hypercubic lattice is a
translate of its flip if and only if it is a Christoffel graph.
This is joint work with Christophe Reutenauer.
Preprint is available at http://arxiv.org/abs/1404.4021.
] [article ] 03/03/2015
Olivier Bouillot Généralisation des nombres et polynômes de Bernoulli aux cas multiples [Slides.pdf ]abstract.htmlLes nombres et polynômes de Bernoulli sont des objets classiques qui apparaissent respectivement lors
du prolongement analytique des fonctions zêta de Riemann et de Hurwitz aux entiers négatifs.
En lien avec la généralisation multiple de ces fonctions, les multizêtas et multizêtas de Hurwitz,
nous allons généraliser les nombres et polynômes de Bernoulli au cas multiple.
Bien qu'il n'y a pas unicité d'une telle généralisation,
nous introduirons un exemple explicite et satisfaisant où nombres
de propriétés importantes des polynômes de Bernoulli se transmettent au cas multiple.
Au passage, cela permet de répondre à une question sur la renormalisation des multizêtas aux entiers négatifs.
] 03/03/2015
Quoc Hoan Ngo Sommes harmoniques et polylogarithmes en les multiindices negatifs (2/2) [abstract.pdf ] 03/03/2015
Gérard Duchamp Asymptotic scales, asymptotic expansions and characters 25/02/2015
Michael Drmota Quasi-random properties of subsequences of sequences generated by finite automataabstract.htmlAutomatic sequences T(n) are the output sequence of a finite automaton, where
the input is the q-adic digital representation of n. The most prominent example
is the Thue-Morse sequence t(n) (that is also the fixed point of the substitution
0 -> 01, 1 -> 10). Automatic sequences have been studied in many diff erent contexts
from combinatorics to algebra, number theory, harmonic analysis, geometry
and dynamical systems. For example, they have a linear subword complexity and
they are almost periodic.
Since the subword complexity is linear the entropy of the related dynamical system is zero. This also means that
they do not behave like a random sequence. However, the situation changes drastically when
one uses proper subsequences of automatic sequences, for example the subsequence along primes or
squares. It is conjectured that the resulting sequences are normal sequences so that
they behave like random sequences (=quasi random sequences).
Recently this property was proved (together with C. Mauduit and J. Rivat)
for the Thue-Morse sequence along the subsequence of squares - and it turns out that this
propery extends to several other automatic sequences and also to subsequences of the form
[n^c], where 1 < c < 4/3. Thus such subsequences of automatic sequences give rise to
a completely new class of pseudo random sequences that can be computed very efficiently.
] 24/02/2015
Michael Drmota Profile of random trees [Slides.pdf ]abstract.htmlThe purpose of this talk is to give a survey on the behaviour of the profile of three different
kind of random trees, namely Galton-Watson trees, search trees and digital trees.
] 17/02/2015
Élie de Panafieu Problèmes de satisfaction de contraintes et graphes inhomogènes 17/02/2015
Quoc Hoan Ngo Sommes harmoniques et polylogarithmes en les multiindices negatifs (1/2) [abstract.pdf ] 10/02/2015
Gaëtan Borot Énumérer les cartes farcies de toute topologie (avec un soupçon de combinatoire analytique)abstract.htmlLes cartes sont des surfaces discrètes construites en recollant le
long de leurs bords des polygônes - l'exemple le plus simple étant les
triangulations. En tant que surfaces orientables, leur topologie est
caractérisée par le nombre de bords n, et le nombre d'anses g. Si l'on
se donne un poids de Boltzmann t_k pour chaque k-gone, l'énumération
des cartes à un bord et de genre 0 est un problème très bien étudié.
Ici, je considèrerai le problème plus général d'énumérer les cartes
farcies: ce sont les surfaces obtenues en a) piochant dans une boîte à
outils pouvant contenir des surfaces à bords polygonaux et de
topologie quelconque ; b) en recollant ces morceaux élémentaires le
long de leurs bords ; c) pondérant l'énumération par des poids de
Boltzmann dépendant du genre et de la longueur des bords de chaque
morceau élémentaire. J'expliquerai notamment qu'il existe une
récurrence universelle sur la caractéristique d'Euler totale 2 - 2g -
n, qui réduit le problème d'énumération en toute topologie à celui des
disques (n = 1, g = 0) et des cylindres (n = 2,g = 0).
] 10/02/2015
Gérard Duchamp Polyzetas, characters and the Euler-Mascheroni constant 03/02/2015
Adrian Tanasa Graph polynomials and relations with physicsabstract.htmlIn the first part of the talk I will introduce the Tutte
polynomial of graphs and explicitly show its relation with
polynomials appearing in the so-called parametric representation of
integrands canonically associated to graphs in quantum field theory.
In the second part of the talk I will show a new proof of the
celebrated property of universality of the Tutte polynomial of graphs
(or matroids), proof which does not require the usual edge induction
arguments. Finally, I will present how this proof generalizes for the
universality property of the Bollobas-Riordan polynomial of ribbon
graphs (or embedded graphs).
] 27/01/2015
Gérard Duchamp Evolution equations in combinatorics and physics 20/01/2015
Francesco Caltagirone On convergence of Approximate Message Passing [Slides.pdf ]abstract.htmlApproximate message passing is an iterative algorithm for compressed
sensing and related applications. A solid theory about the performance and
convergence of the algorithm exists for measurement matrices having iid
entries of zero mean. However, it was observed by several authors that for
more general matrices the algorithm often encounters convergence problems.
In this paper we identify the reason of the non-convergence for measurement
matrices with iid entries and non-zero mean in the context of Bayes optimal
inference. Finally we demonstrate numerically that when the iterative
update is changed from parallel to sequential the convergence is restored.
] 13/01/2015
Johan Nilsson Generalized paper-folding sequences [Slides.pdf ] [abstract.pdf ] 13/01/2015
Gérard Duchamp Séries de Hilbert et noyaux 06/01/2015
ANALCO 2015 / SODA 2015 (San Diego) 06/01/2015
Hoang Ngoc Minh Combinatorics of the Dyson series 16/12/2014
Hsien-Kuei Hwang Dependence and phase change in random m-ary search trees 16/12/2014
Hoang Ngoc Minh 09/12/2014
Adrian Tanasa Asymptotic expansion for random tensor modelsabstract.htmlThree-dimensional random tensor models are a natural generalization of
the celebrated matrix models. The associated tensor graphs, or 3D
maps, can be classified with respect to a particular integer or
half-integer, the degree of the respective graph.
I will present in this talk a combinatorial analysis of the general
term of the asymptotic expansion in N, the size of the tensor, of a
particular random tensor model, the so-called multi-orientable model.
I will then present some enumerative results and show which are the
dominant configurations of a given degree; several examples will also
be given.
] [article ] 09/12/2014
Christophe Tollu Idempotents de Lie et idempotents primitifs (séance interactive) 02/12/2014
Lionel Pournin Le diamètre asymptotique des associaèdres généralisésabstract.htmlLes associaèdres généralisés ont été introduits par Sergey
Fomin et Andrei Zelevinsky dans le cadre de la théorie des algèbres
amassées, et réalisés géométriquement par Chapoton, Fomin et
Zelevinsky. Ils sont associés à n'importe quel groupe de Coxeter fini.
Parmi eux figurent trois familles infinies de polytopes : les
associaèdres de type A (associaèdres usuels), de type B ou C
(cycloèdres), et de type D.
Le diamètre asymptotique des associaèdres de types A, B (ou C), et D
est maintenant connu et cet exposé passera en revue les cas des types
B (ou C), et D. Les preuves ne seront pas données entièrement, mais
seulement esquissées. Quelques questions associées seront finalement
discutées.
] 02/12/2014
Christophe Tollu 25/11/2014
Yeong-Nan Yeh Tutte polynomial, G-parking function and sandpile [abstract.pdf ] 25/11/2014
Christian Lavault Nombres généralisés de Stirling, Bessel, Touchard et Bell dans l'algèbre de Weyl méromorphe (2ème partie) 18/11/2014
Phan Dương Hiệu Cryptographie : Black-box Trace and Revoke Codes [Slides.pdf ] 18/11/2014
Christian Lavault Nombres généralisés de Stirling, Bessel, Touchard et Bell dans l'algèbre de Weyl méromorphe 04/11/2014
Silvia Goodenough On the Heisenberg--Weyl algebra and related sets of Riordan subgroups 28/10/2014
Hoang Ngoc Minh (Pure) transcendence bases in phi-deformed shuffle bialgebras. Application to identify local coordinates in the group of associatorsabstract.htmlEffective construction of pairs of bases in duality in the general co-commutative deformations
of the shuffle co-product allow to identify the local coordinates in the group of associators
leading to the ideal of homogeneous polynomial relations among polyzetas.
] 28/10/2014
Quoc Hoan Ngo 21/10/2014
Mathilde Bouvel A general theory of Wilf-equivalence for Catalan structuresabstract.htmlIt is a commonly observed phenomenon in enumerative combinatorics that
several combinatorial classes share the same enumeration. For any two
classes which seem to have the same enumeration sequence, a natural
problem is to prove that it is indeed the case, ideally with a
bijective proof that allows to map the structure of one class to that
of the other.
Such coincidences of enumeration are called Wilf-equivalences in the
context of pattern-avoiding permutation classes (the definition of
pattern-avoidance will be given during the talk). Wilf-equivalence has
been a popular topic in the research on pattern-avoiding permutations,
from its beginnings in the seventies until now. It is fair to say that
most of the works done so far are specific to given pairs of
equi-numerous classes, thus forming a sort of "case-by-case catalogue"
of the known Wilf-equivalences.
In this talk, we explore a different approach: we are interested in
describing all Wilf-equivalences between permutations classes defined
by the avoidance of two patterns: 231 and an additional pattern p
(w.l.o.g., we can assume that p itself avoids 231). We will explain
that this is one way of phrasing a seemingly more general (but
actually equivalent) question: that of describing all
Wilf-equivalences between classes of Catalan objects subject to one
further avoidance restriction. Such classes are denoted Av(A), A being
a Catalan object.
Our results, to be presented in the talk, are the following.
First, we define an equivalence relation ~ among Catalan objects. Our
main result is that it refines Wilf-equivalence: if A ~ B, then Av(A)
and Av(B) have the same enumeration. The proof is subdivided in
several cases, and it is bijective in all cases but one. We further
conjecture that the converse statement holds, i.e., that this relation
~ coincides with Wilf-equivalence.
Then, we show how to enumerate the number of equivalence classes for
~, hereby providing an upper bound on the number of Wilf-equivalence
classes.
It is also interesting to study a special ~-equivalence class, which
can be understood at a very fine level of details. Our results on this
~-class (called the "main" one) unify and generalize several results
of the literature on Wilf-equivalence.
Finally, we explain how our bijective cases in the proof of the main
theorem can often be refined to provide comparison results between the
enumerations of classes Av(A) and Av(B) when A and B are not
equivalent for ~. A consequence is that the "main" ~-class corresponds
to the largest possible enumeration sequence.
This is joint work with Michael Albert (University of Otago), and a
preprint is available at arXiv:1407.8261.
] [article ] 21/10/2014
Valentin Féray Inclusion/exclusion cycliqueabstract.htmlDans cet exposé (au tableau), je regarderai la série génératrice multivariée des fonctions croissantes sur un ensemble ordonné donné.
Le but est de décrire combinatoirement (à l'aide des diagrammes de Hasse des ensembles ordonnés) les relations entre les séries formelles obtenues.
Je vais d'abord présenter le travail fondamental de Stanley sur les P-partitions qui répond, en quelque sorte, à cette question.
Je donnerai ensuite une seconde réponse, à l'aide de l'opération d'inclusion-exclusion cyclique que j'ai récemment introduite.
] 14/10/2014
Gérard Duchamp Transcendence et algorithme de remplacement 14/10/2014
Van Chiên Bui Struture of polyzetas and algorithms on the bases 07/10/2014
Thierry Monteil Le langage asymptotique des courbes lissesabstract.htmlLe tracé d'une courbe sur une grille produit une suite de pixels consécutifs
qui peut être représentée par un mot sur l'alphabet {droite, haut, gauche,
bas}. Ce codage établit un dictionnaire entre objets géométriques (ou
différentiels) et propriétés combinatoires sur les mots. Par exemple, le
codage des segments de droites correspond aux mots dits 1-équilibrés, qui
sont les facteurs finis des mots sturmiens.
Une méthode classique pour analyser une courbe lisse discrétisée consiste à
décomposer son codage en mots 1-équilibrés maximaux, qui servent alors de
tangentes discrètes. Sans ajout d'hypothèses, les estimateurs de tangentes
ou de courbure associés ne convergent pas nécéssairement lorsque la maille
de la grille tend vers zéro.
Une raison possible est la suivante : certains mots non 1-équilibrés peuvent
apparaître dans le codage de courbes lisses pour des mailles arbitrairement
fines.
Let but de cet exposé est de décrire ce langage et voir ce qu'on peut lui
faire dire.
] 07/10/2014
Séance d'organisation 30/09/2014
Joseph Ben Geloun Polynomials invariants on stranded graphs [Slides.pdf ]abstract.htmlTutte polynomial is a 2-variable polynomial defined on a graph which
satisfies a contraction/deletion recurrence relation. This polynomial
generalizes into the so-called Bollobas-Riordan (4-variable) polynomial for
ribbon graphs which also satisfies a similar recurrence rule. In the recent
Physics literature, there exists a growing interest for a new category of
graphs called rank d stranded graphs. Such graphs encompass simple and
ribbon graph structures and represent simplicial complexes in any dimension
d. I will introduce a genuine 7-variable polynomial on these graph
structures when restricted in rank 3 and when provided with a specific
coloring. The polynomial satisfies a new contraction/cut rule. The procedure
can be certainly extended in any rank.
] [article ] 30/09/2014
Lauren Williams Introduction to cluster algebras (à l'IHP) 23/09/2014
Nguyên Hoàng Nghĩa soutenance de thèse 02/07/2014
Nicolas Basset Génération aléatoire via les langages temporisés [Slides.pdf ]abstract.htmlA chaque langage régulier, on associe la classe (appelée régulière) de permutations ayant
un motif d'ascentes/descentes (a/d) dans ce langage régulier de {a,d}* . Par exemple, on peut définir ainsi les permutations alternantes, les
permutations n’ayant pas deux descentes consécutives, les permutations ayant un nombre pair de
descentes... J’expliquerai un algorithme qui étant donné un automate renvoie une formule close
pour la série génératrice exponentielle de la classe régulière de permutations associée. J’expliquerai
ensuite un algorithme qui permet de générer des permutations aléatoirement et de façon uniforme
les permutations de même longueur de la classe régulière de permutations considérée. Les deux
algorithmes sont basés sur une correspondance entre comptage de permutations et volumes de
langages temporisés qui s’explique en terme de polytopes d’ordre et polytopes de chaîne de Stanley.
Les deux algorithmes évoqués ci-dessus sont ainsi obtenus à partir d’algorithmes de calcul
de fonction génératrice des volumes et de génération aléatoire de mots temporisé associés à un
automate temporisé.
] 02/07/2014
Julien David Machines de Łukasiewicz [Slides.pdf ]abstract.htmlDans cette présentation, on s'intéressera à deux sujets a priori distincts.
Le premier concerne la génération aléatoire d'arbres planaires dans
lequel on maîtrise le nombre d'occurrences d'un motif d'arbre.
Le but est, partant d'un motif donné, de produire automatiquement
une grammaire d'arbre dans laquelle les occurrences du motif sont marqués.
Cette grammaire permet directement d'obtenir un générateur aléatoire
en utilisant la méthode récursive, mais permet également d'obtenir
une série génératrice bivariée.
Le second est une présentation d'une famille de grammaires d'arbres
et des automates qui y sont associés, appelés machines de Lukasiewicz.
Cette famille fut utilisé pour résoudre le premier problème.
Il s'agit d'une généralisation des grammaires d'arbre régulières.
Si ces grammaires et les machines associés ont des propriétés de clôtures décevantes,
on a pu décrire un algorithme de minimisation pour les machines déterministes.
] 02/07/2014
Marie-Pierre Béal Systèmes sofiques-Dyck et fonctions zêtas [Slides.pdf ]abstract.htmlLes systèmes dynamiques symboliques sont des suites bi-infinies de symboles
dont les facteurs finis évitent un ensemble de mots finis donné. Nous
présentons les systèmes appelés sofiques-Dyck. Ces systèmes sont une
généralisation des systèmes Markov-Dyck introduits par Krieger et
Matsumoto. Nous montrons que ces systèmes de séquences sont exactement les
systèmes dont le langage des facteurs finis est un langage de mots
imbriqués (nested words). Nous calculons la fonction zêta, qui compte les
séquences périodiques du système, pour un système sofic-Dyck.
(Travaux avec Michel Blockelet et Catalin Dima)
] 02/07/2014
CALIN
Quelques résultats de "combinatoire-théorie des langages" récents ou anciens ou futurs ! 02/07/2014
Gérard Duchamp Marcel-Paul Schützenberger et les monoïdesabstract.htmlMarcel-Paul Schützenberger était un fan du monoïde plaxique et aussi
des monoïdes de commutation : souvenirs et réminiscences.
] 02/07/2014
journée "combinatoire et théorie des langages" à Paris 13 (et clôture de cette année de séminaires CALIN !) 01/07/2014
ANR Magnum
journée ANR Magnum à Marne (9h30 Chaim Goodmann-Strauss , 11h Julien Clément , 12h discussions, 12h30 buffet, 14h30 soutenance de Sven de Félice , 16h30 pot et discussions sur Magnum)abstract.htmlLe 1er juillet aura lieu à Marne une journée de l'ANR MAGNUM, avec des exposés le matin et la soutenance de thèse de Sven De Félice l'après-midi.
Voilà le programme de la journée :
9h30 Accueil,
10h Chaim Goodman-Strauss (Univ. Arkansas),
11h Julien Clément (GREYC),
12h Discussions,
12h30 Buffet,
14h30 Soutenance de thèse de Sven De Félice,
16h30 Pot de thèse et discussions sur Magnum.
Cela a lieu dans la salle de séminaire 4B08R, au 4eme étage du
batiment Copernic. Pour venir, descendre à la station Noisy-Champs
du RER A (direction Marne-la-vallee ou Torcy) et suivre le plan :
http://www.u-pem.fr/universite/presentation/plans-dacces/plan-du-campus/
] 27/06/2014
Ladji Kané Soutenance de thèse 24/06/2014
Lucas Gerin Exposants d'échelle pour un modèle (très simplifié) de percolation de premier passage 24/06/2014
Marie Théret Retour sur le théorème de forme en percolation de premier passage 24/06/2014
Jean-Christophe Mourrat Temps de survie du processus de contact sur les graphes aléatoires réguliers 24/06/2014
Olivier Garet Processus de contact en milieu aléatoire 24/06/2014
Ellen Saada Un théorème de forme asymptotique pour un modèle de propagation d'épidémie >2 24/06/2014
Journée MathStic (LIPN-LAGA) 17/06/2014
Conférence AofA'2014 @Jussieu, du 16 au 20 juin 10/06/2014
pôt départ à la retraite de Silvia Goodenough 10/06/2014
Christophe Tollu Grassmanniennes, positivité et positroïdes (deuxième partie, d'après A. Postnikov)abstract.htmlLes positroïdes sont des matroïdes qui sont liés à l'étude de la partie positive des variétés grassmanniennes. Ils sont depuis quelques années l'objet de nombreuses études, en combinatoire, en géométrie et même en physique. L'exposé retracera le chemin qui, des variétés grassmanniennes, a mené à leur définition. On commencera par de nombreux rappels et on s'appuiera surtout sur les travaux d'A. Postnikov.
] 03/06/2014
Christophe Tollu Grassmanniennes, positivité et positroïdes (d'après A. Postnikov)abstract.htmlLes positroïdes sont des matroïdes qui sont liés à l'étude de la partie positive des variétés grassmanniennes. Ils sont depuis quelques années l'objet de nombreuses études, en combinatoire, en géométrie et même en physique. L'exposé retracera le chemin qui, des variétés grassmanniennes, a mené à leur définition. On commencera par de nombreux rappels et on s'appuiera surtout sur les travaux d'A. Postnikov.
] 27/05/2014
Éric Fusy La fonction à deux points et à trois points pour les quadrangulations et cartes [Slides.pdf ]abstract.htmlPour une famille F de cartes planaires on appelle "fonction à k points" la série génératrice de comptage des cartes de F avec k points
marqués dont les distances deux à deux sont prescrites. On sait depuis les résultats de Bouttier, Di Francesco et Guitter
(s'appuyant sur une bijection de Schaeffer) que la fonction à 2 points des
quadrangulations admet une expression explicite, et des réultats plus
récents de Bouttier et Guitter (s'appuyant sur une bijection de Miermont)
ont établi une expression explicite pour la fonction à trois points des quadrangulations.
Nous passerons en revue ces résultats et montrerons comment on peut exploiter une bijection récente due à Ambjorn et Budd pour établir des
expressions explicites pour les fonctions à deux points et à trois points des cartes générales.
Travaux en commun avec Jérémie Bouttier et Emmanuel Guitter
] 27/05/2014
Gérard Duchamp Prolongement des fonctions holomorphes et des sommes harmoniques (séance interactive) 20/05/2014
Raoul Santachiara Conformal field theory approach: combinatorial aspects and applications in critical geometryabstract.htmlA two-dimensional system enjoys conformal symmetry when the
invariance under rescaling and rotations is enhanced to invariance
under any conformal (i.e. analytic and invertible) mapping. The
conformal field theory (CFT) approach aims to find the solutions of
the infinite set of equations imposed by conformal invariance. This
approach has been successfully employed in diverse areas of physics
and mathematics for almost thirty years. We will survey the basics
ideas behind the CFT approach. We will adress some recent results
concerning the representation of Virasoro algebras and its relations
with Benjamin-Ono and Calogero-Moser integrable models. We finally
show new results on conformally invariant random fractals.
] 20/05/2014
Christophe Tollu Grassmanniennes, positivité et positroïdes (d'après A. Postnikov)abstract.htmlLes positroïdes sont des matroïdes qui sont liés à l'étude de la partie positive des variétés grassmanniennes. Ils sont depuis quelques années l'objet de nombreuses études, en combinatoire, en géométrie et même en physique. L'exposé retracera le chemin qui, des variétés grassmanniennes, a mené à leur définition. On commencera par de nombreux rappels et on s'appuiera surtout sur les travaux d'A. Postnikov.
] 13/05/2014
Sihem Mesnager Objets combinatoires en cryptographie et en théorie des codes [Slides.pdf ]abstract.htmlLes fonctions courbes ont été introduites par Rothaus et étudiées pour
la première fois par Dillon dans sa thèse. Les fonctions courbes sont
les fonctions booléennes qui sont à distance de Hamming maximale des
fonctions affines. Depuis leur introduction, elles
sont devenues l'un des objets les plus important en cryptographie symétrique. Une
des raisons motivant leur étude est qu'il est recommandé que la
fonction booléenne utilisée pour concevoir un système de chiffrement
symétrique soit une fonction courbe pour pouvoir résister de manière optimale
aux attaques par corrélation rapides. En plus de cette importance
cryptographique, les fonctions courbes ont la propriété fascinante que
leurs supports sont des objets combinatoires intéressants. Leurs supports
forment des ensembles à différence, appelés ensembles à
différence de Hadamard. Parmi les familles de fonctions courbes, il en
est une qui pourrait avoir une importance grandissante dans les années
à venir : les fonctions hyper-courbes (introduites par Youssef et Gong
en 2001). Les fonctions hyper-courbes sont des fonctions courbes qui
ont la propriété d'être aussi à distance maximale des permutations
polynomiales. Très récemment, il a été mis en lumière que ces
fonctions étaient en relation étroite avec des objets géométriques
intéressants: les hyperovales.
Dans cet exposé, nous présenterons un résumé des résultats les plus
importants et de nos apports à l'étude des fonctions booléennes
courbes en illustrant les liens possibles entre les fonctions courbes et
des objets combinatoires et géométriques cités précédemment. Nous
présenterons aussi le lien entre les fonctions courbes et la théorie
des codes et plus particulièrement entre certaines fonctions
vectorielles courbes et les codes minimaux (dont les propriétés
combinatoires peuvent être exploitées par les systèmes de partage
de secret).
] 13/05/2014
Van Chiên Bui Studying construction of polyzetas 06/05/2014
Lionel Pournin Sur les diamètres de certains graphes de flipsabstract.html Considérons une surface orientable S de genre g avec k>0
bords. Plaçons un ensemble E de n points sur S de manière que chaque
bord contienne au moins un de ces points. Le graphe des flips de E est
le graphe G dont les sommets sont les triangulations de E et dont les
arêtes joignent deux triangulations qui peuvent être transformées
l'une en l'autre par un flip (cette opération consiste à échanger les
diagonales d'un quadrilatère). Le graphe G est connexe. Si on
considère les triangulations de E à homéomorphisme près, les sommets
de E étant marqués, le diamètre de ce graphe est borné.
Lorsque S est un disque dont le bord contient tous les points de E, G
est le graphe de l'associaèdre de dimension n-3. Il a été montré
récemment que le diamètre de ce graphe est 2n-10 dès que n est
supérieur à 12. La preuve de ce résultat sera esquissée. Plusieurs
autres résultats sur le diamètre de G seront ensuite donnés et
discutés dans le cas où S n'est pas un disque.
] 06/05/2014
Quoc Hoan Ngo A scheme of noncommutative combinatorial number theory and physics 29/04/2014
exposés ANR Magnum à P6: O. Bodini & A. Sportiello 15/04/2014
Ha Duong Phan Some algebraic structures on chip firing gameabstract.htmlThe chip firing game is a discrete dynamical model on
graphs which was first defined by D. Dhar (1990) and by A. Björner, L.
Lovász and W. Shor (1991). The model has various applications in many
fields of science such as physics, computer science, social science and
mathematics. Recently, this model is used as a tool to study many
properties of graphs and it was proved to be related to subjects of graph
theory, such as Laplacian matrix, Tutte polynomial, spanning tree or
graphic matroid, etc. In this talk, I will present some algebraic
structure raised on this model.
] 15/04/2014
Ladji Kane Factorisations tangentes à l'identité 08/04/2014
Gleb Koshevoy A Hopf algebra structure on positroids 08/04/2014
Réunion des CS pour audition MdC et Prof 01/04/2014
Srecko Brlek Sur la structure palindromique des mots [Slides.pdf ]abstract.html En combinatoire des mots finis ou infinis, la nature des motifs qui apparaissent dans un mot donné sont
une des nombreuses manières de déterminer sa complexité. Les calculs de diverses statistiques permettent de mettre en évidence
certaines relations qu'il vérifie.
] 01/04/2014
Alice Jacquot Soutenance de thèse 25/03/2014
Irène Marcovici Autour des automates cellulaires probabilistesabstract.htmlUn automate cellulaire probabiliste (ACP) est une chaîne de Markov sur un espace symbolique.
Le temps est discret, les cellules évoluent de manière synchrone, et le nouvel état de chaque cellule
est choisi de manière aléatoire, indépendamment des autres cellules, selon une distribution déterminée
par les états d'un nombre fini de cellules situées dans le voisinage.
Je présenterai les résultats obtenus au cours de ma thèse sur deux "problèmes inverses" : le premier
consiste à étudier les ACP ayant des mesures invariantes de forme produit de Bernoulli ;
le second est le problème de la classification de la densité, qui consiste à trouver un AC(P) dont l'évolution
permette de distinguer une configuration initiale sur l'alphabet binaire tirée selon une mesure de Bernoulli
de paramètre inférieur ou supérieur à 1/2, et que nous avons résolu sur les grilles
de dimension supérieure ou égale à 2 et sur les arbres.
] 25/03/2014
Wojciech Mlotkowski Noncommutative probability (3/3): free infinite divisibility 18/03/2014
Journées Aléa (17-21 mars)18/03/2014
Ladji Kane Combinatoire des q-déformations de la base de Poincaré-Birkhoff-Witt-Lyndon (2/2)abstract.htmlSoit S_w^{(q)} une base construit avec la même relation de réccurence et avec la même condition iniatiale que la base S_w.
Soit P_w^{(q)} la base duale de la base S_w^{(q)}.
Nous allons montrer qu'une q-déformation de la base de Poincaré-Birkhoff-Witt-Lyndon P_w^{(q)} est aussi multiplicative.
Cette deuxième séance sera consacrée à l'examen fin des stastistiques sur le groupe symétrique induite par la q-shuffle et au conditions suffisantes de multiplicativité des bases.
] 18/03/2014
Wojciech Mlotkowski Noncommutative probability (2/3): free additive and multiplicative convolutions [Slides.pdf ] 11/03/2014
Matthieu Deneufchâtel Convolution de Dirichlet et énumération de pyramides et espaliers [Slides.pdf ]abstract.htmlNous étudions l’énumération de deux familles de polycubes, les
pyramides et les espaliers, en lien avec une version multi-indexée de la
convolution de Dirichlet.
] 11/03/2014
Wojciech Mlotkowski Noncommutative probability (1/3): noncrossing partitions and free cumulants [Slides.pdf ] 04/03/2014
Moon Duchin Rationality of growth in the Heisenberg groupsabstract.htmlI'll discuss the history of work on the question of how and
whether rationality of growth depends on generators. That is, for a
finitely generated group, one can study the growth function (the number of
words spellable in up to n letters) and its growth series, the associated
generating function. This growth series is itself a rational function when
there is a recursive relationship among the values of the growth function.
It is known that all virtually abelian groups and all hyperbolic groups
have rational growth in any generators, by work of Benson and Cannon
respectively. Work of Shapiro and of Stoll sheds some light on the
situation in nilpotent groups, but shows it to be more complicated-- even
for the second Heisenberg group H_5, some generators give rational growth
but others do not. I'll describe work in progress with Shapiro giving
geometric arguments to establish rationality in all generators for the
classical Heisenberg group H_3.
] 04/03/2014
Wojciech Mlotkowski Free product of representations 04/03/2014
Ladji Kane Combinatoire des q-déformations de la base de Poincaré-Birkhoff-Witt-Lyndon (1/2)abstract.htmlSoit S_w^{(q)} une base construite avec la même relation de réccurence et avec la même condition iniatiale que la base S_w, mais en utilisant une déformation du shuffle.
Soit P_w^{(q)} la base duale de la base S_w^{(q)}.
Nous allons proposer une démonstration du fait que cette q-déformation de la base de Poincaré-Birkhoff-Witt-Lyndon P_w^{(q)} est aussi multiplicative.
] 25/02/2014
Quentin de Mourgues A left/right dynamic on permutationsabstract.htmlSoit s une permutation dans Sigma_n.
Soit i(s)=s(1), j(s)=s^{-1}(1),
Soit C_k le cycle 1>2>...>(k-1)>1 (k,k+1,..,n points fixes).
On definit L et R comme suit:
L(s) = C_{j(s)}.s
et
R(s) = s.C_{i(s)}^{-1}
Il est facile de voir que L et R sont inversibles, la dynamique L/R partitionne donc Sigma_n en classes d'équivalence qui sont des graphes orientés
uniformes (une arête entrant/sortant par "couleur" L et R) fortement connexes.
Dans cet exposé, on étudiera ces classes : leur nombre, leur taille, leur structure, etc.
] 25/02/2014
Gleb Koshevoy Cluster fansabstract.html One of the main motivation of S.Fomin and A.Zelevinsky
for introducing cluster algebras was the desire to
provide a combinatorial framework to understand the structure of ''dual
canonical bases'' in coordinate rings of various algebraic varieties related to semisimple groups. For a finite cluster algebra, they show that the cluster complex can be implemented as a simplical fan in the vector space span by the simple roots of the corresponding Lie algebra.
We show that the cluster complex for cluster algebra of the base affine space for GL(n) can be implemented
as a simplicial fan in the space span by interval one-column semistandard Young tableaux filled in the alphabet {1,...,n}.
For n>6, such a fan contains infinitely many cones and its support covers semistandard Young tableaux corresponding to
real elements of the dual canonical basis. For types ADE, cluster complexes of the corresponding finite cluster algebras are
subfans of our cluster complex with appropriate n's.
] 18/02/2014
Christophe Tollu [Slides.pdf ] [abstract.pdf ] 12/02/2014
Journées Combinatoires de Bordeaux (12-14 février 2014)12/02/2014
Journées Holonomes (12-14 février 2014)11/02/2014
Michele Pagani Petit voyage autour des sémantiques quantitatives de la logique linéaireabstract.htmlUne sémantique dénotationelle interprète les types de données (comme
Bool ou Int) par des espaces mathématiques (posets, treillis,
structures algébriques) et les programmes par des fonctions sur ces
espaces. L'intérêt d'une telle interprétation étant de donner une
description du comportement opérationnel des programmes qui fait
abstraction du langage dans lequel les programmes sont écrits.
Les sémantiques quantitatives sont en particulier les sémantiques
dénotationelles issues de la logique linéaire, où les types de données
sont interprétés par des espaces vectoriels (ou, plus généralement,
des modules), les programmes qui utilisent exactement une fois leurs
données d'entrée deviennent des fonctions linéaires (au sens
algébrique), alors que les programmes qui utilisent leurs ressources
un nombre indéterminé de fois (comme les programmes récursifs ou les
programmes utilisant l'instruction while, par exemple) sont
interprétés par des fonctions analytiques, approximables par des
polynômes, qui représentent des calculs partiels.
Ces sémantiques sont particulièrement naturels pour décrire des
programmes non-déterministes, voire probabilistes ou quantiques,
l'addition exprimant une sorte de superposition des états élémentaires
et les scalaires associant une estimation quantitative à une telle
superposition.
Dans cet exposé, je chercherai à donner une intuition de
l'interprétation des programmes via quelques exemples de sémantiques
quantitatives et à donner un aperçu des résultats récemment
obtenus, en particulier dans le cadre des langages fonctionnels
probabilistes.
] 11/02/2014
Christophe Tollu Algèbre de Hopf de Zelevinsky : algèbres PSH (2/3)abstract.htmlLes algèbres PSH sont des algèbres de Hopf (sur les rationnels ou les réels) autoduales qui ont une base pour laquelle les constantes de structures sont positives. Le premier exposé sera consacré à quelques résultats de structure, et le deuxième à l'usage que Zelevinsky a fait de ces algèbres en théorie des représentations.
] 04/02/2014
Gérard Duchamp A lemma about angular independence (Discussion) 28/01/2014
Adeline Pierrot Combinatoire et algorithmique dans les classes de permutationsabstract.htmlCet exposé donnera un aperçu du domaine de recherche accessible et
dynamique des permutations à motifs exclus, tout en illustrant dans ce
cadre les interactions fructueuses existantes entre combinatoire et
algorithmique. Un outil clé présenté sera la décomposition par
substitution des permutations, qui est un exemple de décomposition
récursive d'objets discrets utile tant sur le plan combinatoire
qu'algorithmique, et qui fait partie du même cadre général que la
décomposition modulaire des graphes. Une telle décomposition permet de
mettre en évidence la structure des objets étudiés, et de l'exploiter
afin d'obtenir des résultats de nature énumérative, des algorithmes de
génération aléatoire, ou des algorithmes de décision.
] 28/01/2014
Hoang Ngoc Minh Un petit retour sur le prolongement analytique des polylogarithmesabstract.htmlLa repr\'esentation int\'egrale des polylogarithmes, pour $|z|<1$,
$${\rm Li}_{s_1,\ldots,s_r}(z)=\sum_{n_1>\ldots>n_r}\frac{z^{n_1}}{n_1^{s_1}\ldots n_r^{s_r}},$$
permet de le prolonger analytiquement sur ${\mathbb C}^r$.
Aux entiers n\'egatifs, ils sont devenus des fonctions rationnelles en $z$
$${\rm Li}_{-s_1,\ldots,-s_r}(z)=\sum_{n_1>\ldots>n_r} n_1^{s_1}\ldots n_r^{s_r} z^{n_1}\in{\mathbb C}[z,1/z,1/(1-z)]$$
dont le d\'eveloppement de Laurent, en $z=1$, conduisent aux poly-Bernoulli.
] 21/01/2014
Valentin Bonzom Gaussian expectations in random tensor theory from meanders and stabilized-interval-free permutationsabstract.htmlJe m'intéresse à l'espérance de polynômes en des variables aléatoires
tensorielles distribuées selon une gaussienne. Je présenterai
brièvement une famille de polynômes dont les espérances comptent des
nombres de systèmes de méandres, puis je discuterai en détail cette
famille de méandres. Un méandre étant vu comme un collage de deux
systèmes d'arches, il s'agit ici de méandres étiquetés par une
permutation qui détermine un système d'arches à partir de l'autre. Je
montrerai que le nombre de méandres étiquetés par une permutation
donnée se décomposent naturellement en méandres irréductibles,
étiquetés par des permutations qui ne stabilisent aucun sous-interval
(Stabilized-Interval-Free permutations).
] 21/01/2014
Gleb Koshevoy Cluster algebras and subtraction-free computingabstract.htmlUsing cluster transformations we design subtraction-free algorithms for computing Schur
functions and their skew, double and supersymemtric analogues, for generating spanning trees and arborescences polynomials. The latter
provides an exponential complexity gap between circuits admitting arithmetic operations
+, x, / versus +, x. In addition, we establish an exponential complexity
gap between circuits admitting +, -, x, / versus +, x, /. Together with
V. Strassen's result on "Vermeidung von Divisionen" this closes a long-standing problem
on comparative complexity power between all possible subsets of operations +,
-, x, /.
(joint work with S. Fomin and D. Grigoriev)
] 21/01/2014
Olivier Bouillot Sur la notion de polynômes de Bernoulli multiple [abstract.pdf ] 14/01/2014
Olivier Mallet Convolution de Dirichlet et énumération de pyramidesabstract.htmlDans cet exposé, on introduit deux familles de polycubes : les
pyramides et les espaliers. On calcule les séries génératrices
ordinaire et de Dirichlet de ces objets à l'aide d'une version
multi-indexée de la convolution de Dirichlet. On s'intéresse ensuite à
une généralisation des pyramides et des espaliers en dimension d
quelconque et on montre que le nombre de pyramides de volume fixé en
dimension d+1 est un polynôme en d. On explique enfin comment
appliquer les techniques mises en œuvre ici à d'autres familles de
polycubes.
] 14/01/2014
Ladji Kane Combinatoire des q-déformations de la base de Poincaré-Birkhoff-Witt-Lyndonabstract.htmlSoit Sw (q) une base construite avec la même relation de récurrence et avec la même condition initiale que la base Sw .
Soit Pw (q) la base duale de la base Sw (q) .
Nous allons montrer que cette q-déformation de la base de Poincaré-Birkhoff-Witt-Lyndon Pw (q) est aussi multiplicative.
] 07/01/2014
Pierre-Étienne Meunier Pavages auto-assemblants avec et sans coopérationabstract.html Les pavages auto-assemblants sont un modèle de formation de structures moléculaires, dans lequel on peut
simuler des machines de Turing. Il s'agit essentiellement d'une modification des tuiles de Wang, où l'on rajoute un mécanisme de formation des pavages.
Je présenterai dans cet exposé deux résultats de séparation entre deux variantes de ce modèle :
le modèle coopératif, où certaines tuiles ne peuvent s'assembler avec le reste du pavage
que si plusieurs de leurs côtés correspondent, et le modèle non-coopératif, où toutes les tuiles peuvent s'assembler si au moins un de leurs côtés correspond.
] 17/12/2013
Christophe Tollu Algèbre de Hopf de Zelevinsky (1/3) 10/12/2013
Nicolas Curien Sur la structure conforme des cartes planaires aléatoiresabstract.htmlUne triangulation est un graphe (planaire, fini connexe) dessiné proprement
dans la sphère de dimension 2 dont toutes les faces sont des triangles.
On considère une triangulation aléatoire T_n choisie uniformément dans
l'ensemble de toutes les triangulations à n faces.
La structure métrique de T_n munie de la distance de graphe a été étudiée
en profondeur récemment.
En particulier, Le Gall (voir aussi Miermont) a prouvé que T_n
renormalisée par n^{-1/4} converge vers une surface aléatoire
fractale appelée la carte brownienne.
Dans cet exposé nous nous intéresserons à un autre aspect des
triangulations aléatoires. En effet, $T_n$ peut naturellement être munie
d'une structure de surface de Riemann et l'on peut ainsi étudier sa
"structure conforme" qui est censée être très liée au champs libre
gaussien en dimension 2. Je présenterai un chemin pour l'étude de cette structure
conforme fondé sur l'exploration markovienne des cartes planaires à l'aide
d'un processus SLE_6.
] 10/12/2013
Guillaume Chapuy Diamant aztèque, pyramides, et pavages pentus de Z^2abstract.htmlJe parlerai de modèles de pavages par dominos de certaines régions du
plan que nous appelons les «pavages pentus». Ces modèles contiennent
plusieurs classes de pavages pour lesquelles des propriétés
remarquables (énumératives et probabilistes) avaient été obtenues,
notamment le «diamant aztèque» et les «partitions pyramides». Nous
élucidons leur structure combinatoire en les mettant en correspondance
avec des suites de partitions entrelacées, faisant ainsi le lien avec
les «processus de Schur» introduits par Okounkov et Reshetikhin. La
méthode permet non seulement une compréhension unifiée des formules
d'énumération, et leur généralisation à une famille infinie de
modèles, mais également le calcul de fonctions de corrélation entre
particules, ouvrant potentiellement la voie à l'étude unifiée des
formes limites (théorèmes de type «cercle arctique»). Notre point de
vue conduit par ailleurs à des algorithmes plaisants de génération
aléatoire.
L'exposé contiendra de nombreuses illustrations et peut-être même une
applet java. Aucun pré-requis n'est nécessaire.
(Travail commun avec Jérémie Bouttier et Sylvie Corteel)
] 10/12/2013
Christian Houdré Comportements asymptotiques dans quelques problèmes de sous-suites communes et/ou croissantesabstract.htmlCet exposé présentera un panorama partiel et quelques résultats
récents sur le comportement asymptotique (moyenne, variance, lois
limites) dans certains problèmes de plus longue sous-suite croissante
et/ou commune.
] 10/12/2013
Olivier Hénard Autour des arbres de coalescenceabstract.htmlLes arbres de coalescence utilisés en phylogénétique sont naturellement
construits depuis les feuilles. Nous posons la question d'une description
de ces arbres depuis la racine. Parmi les arbres de coalescence, les Beta
coalescents constituent une classe d'étude favorite, et des liens récents
avec certaines classes d'arbres combinatoires (arbres récursifs et arbres
binaires) ont récemment permis d'en améliorer la compréhension. Nous
commencerons par rappeler ces constructions alternatives, dues
respectivement à Goldschmidt et Martin, et Abraham et Delmas. Nous
présenterons ensuite notre propre contribution, basée sur la représentation
dite "lookdown".
] 10/12/2013
Journée MathStic/BQR Marmots : 04/12/2013
Uno Takeaki A New Approach to String Pattern Mining with Approximate Matchabstract.htmlFrequent string mining is the problem of finding frequently appearing
strings in a given string database or large text.
It has many applications to string data analysis on strings such as texts,
word sequences, and genome sequences.
The problem becomes difficult if the string patterns are allowed to match
approximately, i.e., a fixed number of errors leads to an explosion
in the number of small solutions, and a fixed ratio of errors violates
the monotonicity that disables hill climbing algorithms, and thus
makes searching difficult.
There would be also a difficulty on the modeling of the problem;
simple mathematical definitions would result explosion of the solutions.
To solve this difficulty, we go back to the motivations to find frequent
strings, and propose a new method for generating string patterns
that appear in the input string many times.
In the method, we first compute the similarity between the strings
in the database, and enumerate clusters generated by similarity.
We then compute representative strings for each cluster, and the
representatives are our frequent strings.
Further, by taking majority votes, we extend the obtained representatives
to obtain long frequent strings.
The computational experiments we performed show the efficiency of both
our model and algorithm; we were able to find many string
patterns appearing many times in the data, and that were long but
not particularly numerous.
The computation time of our method is practically short, such as
20 minutes even for a genomic sequence of 100 millions of letters.
] 03/12/2013
Uno Takeaki Efficient Algorithms for Dualizing Large-Scale Hypergraphsabstract.htmlA hypergraph F is a set family defined on vertex set V.
The dual of F is the set of minimal subsets H of V such that
J \cap H \ne \emptyset for any J in F
The computation of the dual is equivalent to many problems, such as
minimal hitting set enumeration of a subset family, minimal set cover
enumeration, and the enumeration of hypergraph transversals.
In this paper, we introduce a new set system induced by the minimality
condition of the hitting sets, that enables us to use efficient pruning
methods.
We further propose an efficient algorithm for checking the minimality,
that enables us to construct time efficient and polynomial space
dualization algorithms.
The computational experiments show that our algorithms are quite fast
even for large-scale input for which existing algorithms do not
terminate in practical time.
] 03/12/2013
Ladji Kane Combinatoire du q-shuffle 03/12/2013
Quoc Hoan Ngo Lyndon words, polylogarithm functions and the Riemann zeta functions 19/11/2013
Emily Redelmeier Cartography on unoriented surfaces, with applications to real and quaternionic random matrices [Slides.pdf ]abstract.htmlI will discuss the cartographic machinery (encoding of maps
on surfaces by permutations) on unoriented surfaces. I will discuss
how these appear in calculations with real and quaternionic random
matrices, and their connections with other combinatorial objects
associated with these objects, such as the hyperoctahedral group and
matricial cumulants. I will present some results in asymptotic
second-order freeness which may be approached using these objects.
] 19/11/2013
Gérard Duchamp Infiltration 14/11/2013
James Ryan Melons are branched polymers [Slides.pdf ]abstract.htmlMelonic graphs constitute the family of graphs arising at leading
order in the 1/N expansion of tensor models. They were shown to lead
to a continuum phase, reminiscent of branched polymers. We show here
that they are in fact precisely branched polymers, that is, they
possess Hausdorff dimension 2 and spectral dimension 4/3.
] 14/11/2013
Matti Raasakka Next-to-leading order in the large N expansion of the multi-orientable tensor model [Slides.pdf ]abstract.htmlAfter providing some background and motivation for random tensor
models and their large N expansion, I will discuss recent results on
the next-to-leading order of the large N expansion for the
multi-orientable tensor model. I will describe the class of Feynman
tensor graphs contributing to this order in the expansion, and the
characteristic properties of the next-to-leading order series for this
model. These results represent the first step towards the larger goal
of defining an appropriate double-scaling limit for the
multi-orientable tensor model.
] 14/11/2013
Gilles Schaeffer Regular colored graphs of positive degree [Slides.pdf ]abstract.htmlRegular colored graphs are dual representations of pure colored
D-dimensional complexes. These graphs can be classified with respect
to an integer, their degree, much like maps are characterized by the
genus. We analyse the structure of regular colored graphs of fixed
positive degree and perform their exact and asymptotic enumeration. In
particular we show that the generating function of the family of
graphs of fixed degree is an algebraic series with a positive radius
of convergence, independant of the degree. We describe the singular
behavior of this series near its dominant singularity, and use the
results to establish the double scaling limit of colored tensor models.
] 14/11/2013
Vincent Vargas Critical and dual Gaussian multiplicative chaos [Slides.pdf ]abstract.htmlThe theory of Gaussian multiplicative chaos enables to make
sense of random measures defined formally by the exponential of a
Gaussian
Free Field (and more generally any logarithmically correlated field in
all
dimensions). These random measures are conjectured to be the scaling
limit
of random planar maps coupled to a CFT and conformally mapped to the
sphere or the upper half plane.
The construction of the measures involve a parameter gamma related to
the
central charge c of the CFT. The classical construction does not settle
the question of constructing the measure for c=1 or equivalently
gamma=2
as it yields a vanishing measure. In this talk, I will explain the
appropriate construction and some properties of Gaussian multiplicative
chaos at criticality, i.e. for gamma=2. If time permits, I will also
explain the construction of the dual measure (gamma larger than 2) and
how
to make sense of the KPZ equation in this context.
] 14/11/2013
Omid Amini Coloriage des graphes sur les surfacesabstract.htmlJe commencerai par introduire le concept de S-coloriage de graphe :
étant donné un sous-ensemble S(v) de voisins de v pour tout sommet v d'un
graphe G, c'est un coloriage propre des sommets de G tel que, en outre,
les sommets qui appartiennent ensemble à un même S(v) pour un sommet v reçoivent des couleurs différentes.
Ceci généralise à la fois le concept de coloriage du carré de graphe et
le coloriage cyclique des graphes plongés.
] 14/11/2013
Journée "cartes combinatoires" (PEPS "Cartes 3D" et BQR P13 "Combinatoire algébrique") : 12/11/2013
Jérémie Bouttier Distances in random planar maps and discrete integrability [Slides.pdf ]abstract.htmlMetric properties of random maps (graphs embedded in surfaces) have
been subject to a lot of recent interest. In this talk, I will review
a combinatorial approach to these questions, which exploits bijections
between maps and some labeled trees. Thanks to an unexpected
phenomenon of ``discrete integrability'', it is possible to enumerate
exactly maps with two or three points at prescribed distances, and
more. I will then discuss probabilistic applications to the study of
the Brownian map (obtained as the scaling limit of random planar maps)
and of uniform infinite planar maps (obtained as local limits). If
time allows, I will also explain the combinatorial origin of discrete
integrability, related to the continued fraction expansion of the
so-called resolvent of the one-matrix model. Based on joint works with
E. Guitter and P. Di Francesco.
] 12/11/2013
Hoang Ngoc Minh Mathematical renormalization in quantum electrodynamics via noncommutative generating series [Slides.pdf ]abstract.htmlWe are focusing on the approach by noncommutative formal power series in order to study combinatorial aspects of the renormalization of solutions of nonlinear differential equations with three regular singularities involved in QED (quantum electrodynamics).
] 05/11/2013
Vincent Pilaud Associaèdres d'arbres signésabstract.htmlUn associaèdre est un polytope dont les sommets correspondent aux triangulations d'un polygone convexe et dont les arêtes correspondent aux flips entre ces
triangulations. J.-L. Loday en a donné une réalisation particulièrement élégante qui a été généralisée ensuite dans deux directions : d'un côté par C. Hohlweg et C.
Lange pour obtenir de multiples réalisations de l'associaèdre paramétrées par une séquence de signes, et de l'autre par A. Postnikov pour obtenir une réalisation des
associaèdres de graphes de M. Carr et S. Devadoss. Le but de cet exposé est de présenter une généralisation commune de ces constructions aux associaèdres d'arbres
signés. Nous présenterons aussi les riches propriétés combinatoires et géométriques des polytopes qui en résultent. L'exposé sera illustré par le cas de l'associaèdre
classique, dont l'interprétation en termes d'épine dorsale (arXiv:1307.4391, travail en commun avec C. Lange) est le fil directeur de ce travail.
] 05/11/2013
Collectif Discussion informelle sur Schur et les fonctions symétriques 29/10/2013
Bernhard Gittenberger Random Boolean functions generated by random Boolean expressions [Slides.pdf ]abstract.htmlWe will investigate the probability distribution on the set of Boolean
functions in n variables if a Boolean function is generated by a large
Boolean expression drawn uniformly at random from all expressions of
the same size. We show that a precise quantitative relation between
the probability of a function and its complexity which is defined as
the minimal size of an expression representing the function.
] 22/10/2013
Aléa in Europe School 22/10/2013
Séance à la mémoire d'Alain Lascoux abstract.htmlUne bien triste nouvelle, ce 19 octobre, Alain Lascoux nous a quitté.
Formé comme un spécialiste de géométrie algébrique, puis collaborateur de Marcel-Paul Schützenberger,
il avait consacré toute sa vie de chercheur à mettre au jour et à
exploiter algorithmiquement les aspects combinatoires de certaines
questions d'algèbre, de théorie des représentations et de géométrie.
Plusieurs membres de l'équipe l'ont longuement côtoyé, à Jussieu, à
Marne-la-Vallée ou pendant les réunions semestrielles du Séminaire
Lotharingien de Combinatoire ; nous ne pouvons que
dire que samedi dernier, la combinatoire algébrique a perdu un de ses
maîtres, et avec lui un peu de ses couleurs et de son mordant.
Nous dédions notre traditionnelle séance du séminaire de l'équipe CALIN
(dont Alain fut l'un des parrains scientifiques) à sa mémoire.
] 15/10/2013
Jeremy Lovejoy Le rang d'une suite unimodale et fonctions theta partiellesabstract.htmlIl existe des égalités inattendues autour du rang d'une
suite unimodale, telle que U(1,5,5n+3) = U(2,5,5n+3), où U(t,m,n) est
le nombre de suites unimodales de poids n avec rang congru à t modulo
m. De telles égalités rappellent celles pour le rang d'une partition
qui ont été observées par F. Dyson et qui sont liées aux formes
modulaires et mock modulaires. Dans le cas des suites unimodales, il
n'y a pas cette structure modulaire ; la démonstration dépend d'une
identité de fonctions thêta partielles due à Ramanujan. Ceci est un
travail en commun avec B. Kim (Séoul).
] 15/10/2013
Nguyên Hoàng Nghĩa Structure constants and freeness 08/10/2013
Olivier Carton Normalité et automates [Slides.pdf ]abstract.html We strengthen the theorem that establishes that deterministic finite
transducers can not compress normal infinite words. We prove that, indeed,
non-deterministic finite transducers, even augmented with a fixed number of
counters, can not compress normal infinite words. However, there are
push-down non-deterministic transducers that can compress normal infinite
words. We also obtain new results on the preservation of normality with
automata selectors. Complementing Agafonov's theorem for prefix selectors,
we show that suffix selectors also preserve normality. However, there are
simple two-sided selectors that do not preserve normality.
] 08/10/2013
Collectif Réunion de programme et lissage du phi-shuffle (2ème partie) [article ] 01/10/2013
Nicolas Thiéry Étude de chaînes de Markov à l'aide de représentations de monoïdesabstract.htmlÉtude de chaînes de Markov à l'aide de représentations de monoïdes
La théorie des représentations des groupes finis est un sujet
classique. Dans le cadre plus général des monoïdes finis, la théorie
est plus récente et a priori plus complexe. Cependant il existe des
classes de monoïdes où, comme pour les groupes, la théorie se
simplifie et fait surgir de la combinatoire, ce qui ouvre la porte à
des applications.
Dans cet exposé, nous présenterons brièvement les éléments de la
théorie en mentionnant quelques développements algorithmiques récents
[1], et décriront une application typique à l'étude d'une chaîne de
Markov sur des tas de sable à écoulement orienté [2]. La démarche
exploratoire sera illustrée par quelques calculs typiques avec le
logiciel Sage.
Refs:
] [article ] 01/10/2013
Collectif Réunion de programme et lissage du phi-shuffle [article ] 24/09/2013
Matti Raasakka Connes-Kreimer combinatorial Hopf algebra for the Ben Geloun-Rivasseau tensor field modelabstract.htmlThe Ben Geloun-Rivasseau quantum field theoretical model is the first tensor model shown to be perturbatively renormalizable. We define here an appropriate Hopf algebra describing the combinatorics of this new tensorial renormalization. The structure we propose is significantly different from the previously defined Connes-Kreimer combinatorial Hopf algebras due to the involved combinatorial and topological properties of the tensorial Feynman graphs. In particular, the 2- and 4-point function insertions must be defined to be non-trivial only if the superficial divergence degree of the associated Feynman integral is conserved.
] 24/09/2013
Bérénice Oger Action of the symmetric groups on the homology of the hypertree posetsabstract.htmlThe set of hypertrees on n vertices can be endowed with a poset structure. This poset has been used by McCammond and Meier to study the group of motions of the trivial link, which is an analogue of the braid group. They also proved that this poset is Cohen-Macaulay and computed the dimension of its only homology group. After a short introduction on this topological context, we explain how we used the theory of species to compute the action of the symmetric group on this homology group. We then link it with the PreLie operad.
] 24/09/2013
Emily Burgunder Kontsevich graph complexesabstract.htmlKontsevich proved that the Lie homology of symplectic Hamiltonians can be encoded as the homology of a Hopf bialgebra of graph complex attached to the commutative world. In this talk we will see some generalisation of this theorem : commutative world being replaced by operad, symplectic by a classical group, and we can consider Lie homology or its lifting to Leibniz homology.
] 24/09/2013
Samuele Giraudo From PROs to combinatorial Hopf algebrasabstract.htmlThere is a well-known natural functorial construction which, from a set-operad, produces a Hopf algebra. We extend this construction to the category of PROs with some extra properties. By this generalization, we retrieve, among other, the Hopf algebra of noncommutative symmetric functions in various bases and the noncommutative Faà di Bruno Hopf algebra. We also obtain new ones, as some Hopf algebras involving forests, heaps of pieces, and some kinds of combinational circuits. All these Hopf algebras are similar in a sense to the Connes-Kremier Hopf algebra. In this talk, we shall recall some background about PROs, then present the construction associating a Hopf algebra with a PRO, and finally, review some examples of applications.
] 24/09/2013
Journée MathStic
Trees and graphs (from algebraic combinatorics to topology and random tensor models): 17/09/2013
Thé combinatoire et réunion d'équipe 17/09/2013
Thierry Monteil Pavages : quantifier l'aperiodicité d'un jeu de tuilesabstract.html Un jeu de tuiles de Wang est un ensemble fini de carrés unités dont on a
colorié chaque côté. Un jeu de tuiles T pave le plan si celui-ci peut être
recouvert par des translatés de copies d'éléments de T (selon Z^2), de sorte
que les arêtes en contact de deux tuiles adjacentes soient de même couleur.
Un jeu de tuiles est dit apériodique s'il pave le plan mais si aucun pavage
obtenu n'est invariant par une translation. La plupart des jeux de tuiles
apériodiques sont construits de façon autosimilaire (via une règle de
substitution).
Le but de cet exposé est d'introduire des invariants permettant de
quantifier le niveau d'apériodicité d'un jeu de tuiles de Wang. L'un des
invariants est de nature topologique, l'autre est métrique. Ils reposent sur
la manière dont le jeu de tuiles pave d'autres objets que le plan. Ces
invariants nous permettent de démontrer que les jeux de tuiles de Kari et
Culik ne sont pas gouvernés par une construction autosimilaire, car trop
apériodiques.
] 17/09/2013
Stéphane Fischler Valeurs de G-functionsabstract.htmlUne sous-classe importante des fonctions holonomes
est la classe des G-fonctions (définie par Siegel), qui jouent notamment un rôle important en théorie des nombres, en physique et en combinatoire.
Une grande question, qui demeure en partie ouverte, est de comprendre de façon fine
la structure de l'ensemble des valeurs prises par ces fonctions en des points algébriques.
Ces valeurs englobent de célèbres constantes mathématiques, comme pi, les polyzêtas,
des valeurs de fonctions hypergéométriques...
Nous montrerons le résultat suivant : toute valeur en un point
algébrique d'une G-fonction peut s'écrire f(1),
où f est une G-fonction à coefficients rationnels
dont le rayon de convergence peut de surcroît être choisi arbitrairement grand.
On démontre aussi d'autres propriétés de ces valeurs de G-fonctions ;
par exemple les constantes de connexion obtenues
en prolongeant des G-fonctions sont de tels nombres.
Il s'agit d'un travail en commun avec Tanguy Rivoal, dédié à la mémoire de Philippe Flajolet.
] [article ] 17/09/2013
Gérard Duchamp Une famille de contrexemples liée à l'infiltration des automatesabstract.htmlIt is now sure that one can show a version
of the CQMM theorem which holds even in presence
of heavy torsion. However the arrow constructed
from the enveloping algebra of the primitive
elements may not be into. There is a strange
connection between the counter-example given
on Mathoverflow and the q -infiltration
product discovered by Luque et al.
] 03/09/2013
Ioannis Michos The support problem and shuffle algebra in positive characteristic 30/07/2013
Hans Porst Universal constructions for Hopf algebrasabstract.htmlStarting from a slightly more abstract definition of Hopf algebras as usual, we present a method towards solutions of universal constructions for Hopf algebras (as, e.g., existence of free and cofree ones). On doing so we propose the use of results of category theory, not just of categorical language.
] 23/07/2013
Gérard Duchamp Vers un modèle unifié des déformations et perturbations ? 23/07/2013
Collectif
Point sur les articles en cours 23/07/2013
Hoang Ngoc Minh Sur la conjecture de Kashiwara-Vergne 10/07/2013
Alice Jacquot Soutenance à mi-parcours 10/07/2013
Ladji Kane Soutenance à mi-parcours 10/07/2013
Nguyên Hoàng Nghĩa Soutenance à mi-parcours 02/07/2013
Permutation Patterns 2013 (1-5 juillet 2013)25/06/2013
FPSAC 2013 (24-28 juin 2013)25/06/2013
Ladji Kane Coefficients de normalisation de la q -base S 18/06/2013
Lenka Zdeborová Where the really hard problems really are? [Slides.pdf ] 18/06/2013
Gérard Duchamp q ij 18/06/2013
Hoang Ngoc Minh Monoides pondérés et critère de Friedrichs 13/06/2013
Journée ANR Magnumabstract.html10h30 Aline Parreau (LIFL)
Une preuve combinatoire du lemme local de Lovasz
] 11/06/2013
Grégory Schehr Extreme statistics of non-intersecting Brownian motions [Slides.pdf ]abstract.htmlNon-intersecting Brownian motions (BMs) have
been the subject of numerous studies both in mathematics and in physics. In addition to their
deep connection with random matrix theory, It was shown that they are at the heart of many
fundamental models of statistical physics, like stochastic growth models or
directed paths in random media. In this talk I will review some
recent results which we have obtained for the extreme statistics,
like the maximal height, of such non-intersecting BMs.
] 11/06/2013
Ladji Kane Preuve complète de la formule des coefficients λi 04/06/2013
Andrew Rechnitzer Combinatorics of the hard-squares model [Slides.pdf ] [article ] 04/06/2013
Ladji Kane q shuffles de déformation et de perturbation28/05/2013
AofA (27-31 mai 2013)23/05/2013
Journée MathStic/BQR Marmots Yueyun Hu (LAGA), Axel Bacher (LIPN), Vladas Sidoravicius (Sao Paulo), Hugo Duminil-Copin (Genève), Guy Fayolle (INRIA)21/05/2013
Jehanne Dousse Une généralisation du théorème de Roth pour les progressions arithmétiquesabstract.htmlLe théorème de Roth établit que pour tout a>0, il exite un entier N tel que tout sous-ensemble de {1,...,N} de cardinal au moins aN contient une progression
arithmétique de longueur 3 (un ensemble de la forme {x,x+r,x+2r} avec x et r des entiers non nuls). Plusieurs autres théorèmes importants de combinatoire additive
concernent les progressions arithmétiques, comme le théorème de Szemeredi ou celui de Green-Tao.
Après une introduction à la combinatoire additive, nous présenterons une généralisation du théorème de Roth aux "d-configurations" (ensembles de la forme {x_i+x_j+a|1<=i<=j<=d}, avec x_1,...,x_d et a des entiers) et nous étudierons son application aux sous-ensembles sans somme.
] [article ] 14/05/2013
Thomas Krajewski Combinatorial Hopf algebraic description of the multiscale renormalization in quantum field theory [article ] 14/05/2013
Petru Valicov Quelques résultats sur les codes identifiantsabstract.htmlUn code identifiant d'un graphe est un sous-ensemble C de sommets
qui est à la fois dominant (tout sommet du graphe a un voisin dans
C ou appartient à C) et séparant (tous les sommets ont un
voisinage distinct à l'intérieur de C).
Dans cet exposé, nous
faisons un tour d'horizon de quelques résultats sur cette notion.
Nous proposons une caractérisation des graphes qui ont le code
minimum de taille n-1, n étant l'ordre du graphe. Également nous
nous intéressons à ce paramètre dans la classe des graphes adjoints.
Si le temps le permet, nous parlerons de la complexité du problème
dans différentes sous-classes des graphes parfaits.
] 14/05/2013
Gérard Duchamp Quasi-déterminants 02/05/2013
Tiago Dinis de Fonseca Le modèle à 6 vertex généralisé et les polynômes de Macdonald [Slides.pdf ]abstract.htmlLes polynômes symétriques jouent, depuis toujours, un rôle assez
important en physique.
Par exemple, il est connu que la « fonction génératrice » du modèle à 6
vertex (remarquablement,
ce modèle est en bijection avec les matrices à signes alternants) est
un polynôme de Schur.
Plus récemment, on a découvert, que la « fonction génératrice » d'une
généralisation de ce
modèle est aussi un polynôme symétrique, plus précisément, un polynôme
de Macdonald.
] 02/05/2013
Aristide Baratin Méthodes combinatoires pour la gravité quantiqueabstract.htmlCertaines approches à la gravité quantique reposent sur une construction combinatoire de l'intégrale fonctionnelle.
Une question centrale dans ce contexte est de savoir comment incorporer, ou éventuellement retrouver dans un régime approprié, les symétries de la théorie classique (invariance par difféomorphismes).
Je présenterai certains aspects mathématiques de ce problème, que j'examinerai sous deux angles complémentaires :
le point de vue des invariants dits de "state sum", où les difféomorphismes de la variété sont remplacés par certaines opérations combinatoires sur des triangulations (mouvements de Pachner).
le point de vue des modèles de matrices, où l'invariance par difféomorphismes est le résultat de la sommation sur une certaine classe de graphes associés à des triangulations.
] 23/04/2013
Gérard Duchamp Combinatoire des idempotents de Lie ou CQMM sans baseabstract.htmlLe théorème (classique) de Cartier-Quillen-Milnor-Moore (CQMM) dit que, en caractéristique zéro, une bigèbre est l'algèbre enveloppante de ses éléments primitifs si et seulement si elle est filtrée positivement.
] 18/04/2013
Journée inaugurale du pôle MathStic de Paris 13abstract.htmlJournée inaugurale du pôle MATHSTIC :
3 laboratoires de l'Institut Galilée (Le LAGA, le LIPN, et le L2TI)
s'associent pour proposer une journée inaugurale du POLE MATHSTIC,
le 18 avril de 9h30 à 17h30 en Amphi A.
9h30 Accueil
] 16/04/2013
Jean Fromentin Sur l'arbre des semigroupes numériques [Slides.pdf ]abstract.htmlUn semi-groupe numérique est une partie de N stable par addition et de complément fini.
D'apparence simple, ces objets conduisent à de nombreux problèmes : problème de Frobenius (ou de rendu de monnaie), conjecture de Wilf, ...
Les semi-groupes numériques peuvent être regroupés par genre, le genre d'un semi-groupe numérique étant le cardinal de son complémentaire dans N. Une question naturelle est alors de déterminer le nombre de semi-groupes numériques de genre donné.
Les valeurs de n_g ont été calculés par Maria Bras Amoros pour g<=52. Sur sa page web, Manuel Delgado donne la valeur de n_55.
Dans cet exposé, après une introduction aux semi-groupes numériques, nous présenteront différentes optimisation algorithmiques permettant d'améliorer les résultats
de Maria Bras Amoros et Manuel Delgado.
] 16/04/2013
Matthieu Deneufchâtel Intégrales itérées 16/04/2013
Christophe Tollu Dynamique des tableaux de Young infinis d'après Romik et Sniady 09/04/2013
Sylvie Corteel Pyramides et diamants [Slides.pdf ]abstract.htmlOn cherche à énumérer des pavages par dominos d'une région obtenus
par flip à partir d'un pavage minimal unique.
Pour cela, on utilise les diagrammes maya, les "vertex operators" et
les fonctions de Schur supersymétriques. On obtient des formules type
"équerre" ; dont des cas particuliers compte les pavages du diamant
aztèque ou les partitions pyramides de Ben Young.
[Travail en commun avec Jérémie Bouttier et Guillaume Chapuy)]
] 02/04/2013
Valentin Bonzom A set of triangulations of manifolds in arbitrary dimensions from multi-graphs with colored edgesabstract.htmlI will talk about families of triangulations of manifolds in arbitrary dimensions which can be represented by multi-graphs with colored edges.
I will focus on an important family of such triangulations, called melonic triangulations, which controls the behavior of integrals over random tensors (a promising approach to quantum gravity). These integrals can be solved by an exact counting of the melonic triangulations. If time permits, I will describe the relation to loop models on random planar maps, and also an interesting family of colored triangulations related to meanders.
] 02/04/2013
Valentin Bonzom Invariants of cellular complexes from twisted cohomology and the Reidemeister torsionabstract.htmlCellular complexes are often used in physics as discretizations of spacetime. An interesting class of amplitudes associated to those complexes are topological invariants. I will present a simple model which relates an integral over some Lie group elements associated to the edges of the complex to the so called combinatorial, or Reidemeister torsion of the complex.
] 26/03/2013
Matteo Silimbani Combinatoire des arbres non ambigusabstract.htmlAu cours de cet exposé, je définirai des nouveaux objets
combinatoires, les arbres non-ambigus. Ces objets peuvent être vus
comme des arbres dessinés sur une grille sous certaines contraintes
et ils sont liés à plusieurs objets combinatoires, comme les
polyominos parallélogrammes et les tableaux boisés définis par Aval, Boussicault
et Nadeau. L'on verra comment l'énumération des arbres non-ambigus
satisfaisant des contraintes supplémentaires permet de donner des
preuves combinatoires élégantes d'identités dues à Carlitz, et à
Ehrenborg et Steingrìmsson. Je montrerai aussi une formule des
équerres pour le comptage des arbres non-ambigus dont l'arbre
sous-jacent est fixé. Enfin, je utiliserai les arbres non-ambigus pour
décrire une bijection très naturelle entre polyominos parallélogrammes
et arbres binaires.
] 26/03/2013
70ème Séminaire Lotharingien de Combinatoire 19/03/2013
Journées Aléa 19/03/2013
Gérard Duchamp Fonctions symétriques noncommutatives, algèbre des descentes et action sur les bigèbres sans graduation ni liberté 12/03/2013
Juanjo Rué Perna Bipartite subfamilies of planar graphs [Slides.pdf ]abstract.html I will survey the techniques used to get asymptotic results for
subfamilies of planar graphs, as well as how to relate this methodology
with the context of map enumeration. In the second part of the talk, I will
explain the ideas behind some on-going projects related to the enumeration
of bipartite subfamilies of graphs.
] 12/03/2013
Andrea Sportiello Algebraic/combinatorial proofs of Cayley-type identities for derivatives of determinants and pfaffians 05/03/2013
Axel de Goursac Combinatorial aspects of the Jacobian conjecture [Slides.pdf ]abstract.htmlWe expose the reformulation of the Jacobian conjecture in terms of the combinatorics of Feynman diagrams of a certain Quantum Field Theory. We will also discuss considerations about Dixmier conjecture and Noncommutative Quantum Field Theory.
] 05/03/2013
Axel de Goursac Quantification de Weyl du supergroupe de Heisenberg et application à la théorie quantique combinatoire des champs [Slides.pdf ]abstract.htmlBy using Kirillov's orbits method and Weyl-type quantization on the Heisenberg supergroup, we construct a non-formal deformation quantization of superspaces. We are led by the theory to introduce new notions such as
Hilbert superspaces and C*-superalgebras. Then, a noncommutative superspace coming from this deformation yields an interpretation of the renormalizable quantum field theory with harmonic term on the Moyal space.
] 26/02/2013
Patrice Ossona de Mendez Un petit survol des grands algorithmes de la théorie des graphes, illustrés via le logiciel libre PIGALE [Slides.pdf ] 26/02/2013
Christophe Tollu Algèbres localement semi-simples et graphes gradués : quelques résultats de baseabstract.htmlUne algèbre A est localement semi-simple si c'est la limite inductive d'une chaîne d'algèbres semi-simples de dimension finie An . On associe à A un graphe gradué (appelé diagramme de Bratteli), qui se construit facilement à partir de la décomposition de chaque An en somme directe d'algèbres (pleine) de matrices. Les diagrammes de Bratteli jouent un rôle de premier plan dans la théorie algébrico-combinatoire des algèbres localement semi-simples. Je présenterai quelques résultats fondamentaux de cette théorie.
] 19/02/2013
Christian Krattenthaler Énumeration exacte et asymptotique de pastèques avec barrièreabstract.htmlLe modèle des promeneurs vicieux (sic!)
a été introduit par Michael Fisher en mécanique statistique en 1984.
De nombreuses variantes ont été étudiées depuis,
en particulier celle que je condidère dans mon exposé :
lorsque qu'il y a une interaction entre ces promeneurs et un mur.
Ce modèle a été originellement proposé par Owczarek, Essam et Brak, qui ont
établi quelques résultats partiels.
Je montrerai comment complètement déterminer le comportement asymptotique
de la fonction de partition correspondante (et celle d'un autre paramètre pertinent).
Nous rencontrerons comme de bien entendu (attendu!) mes chers amis :
déterminants, une bijection de tableau et des séries hypergéometriques.
] 19/02/2013
Olivier Bouillot Les multitangentes, vues à travers les multizêtas de Hurwitzabstract.htmlEn lien avec les multizetas qui généralisent la fonction zeta de Riemann
en plusieurs dimension, il existe deux autres familles apparentées et
naturelles : les multizetas de Hurwitz et les multitangentes. Alors que les
multizetas sont des nombres, les multizetas de Hurwitz et les
multitangentes sont des fonctions méromorphes sur C .
] 12/02/2013
Julien Clément Some patterns in Pierre Nicodème's works [Slides.pdf ] 12/02/2013
Bruno Salvy Newton iteration in computer algebra and combinatorics [Slides.pdf ] 12/02/2013
Alin Bostan Computer algebra for the enumeration of lattice walks [Slides.pdf ] 12/02/2013
Pierre Nicodème Journée en l'honneur du départ à la retraite de Pierre Nicodème 05/02/2013
Shalom Eliahou La conjecture de Hadamard [Slides.pdf ] [article ] 05/02/2013
Axel Bacher Inversion de Lagrange multivariée 29/01/2013
Thierry Combot Initiation à la théorie de Galois différentielle et applications aux fonctions holonomes [Slides.pdf ]abstract.htmlNous présenterons la théorie de Galois différentielle appliquée aux
équations différentielles à coefficients polynomiaux puis aux
équations aux différences. On montrera ensuite comment calculer ces
groupes de Galois, et quels sont les algorithmes disponibles. On
présentera alors les méthodes disponibles pour résoudre ces
équations en introduisant les fonctions liouviliennes. Enfin nous
appliquerons ces méthodes pour l'analyse du comportement
asymptotique des solutions : le groupe de Galois donne en particulier
des relations algébriques a priori sur les constantes apparaissant
dans ces développements asymptotiques, et permettent dans le cas
liouvillien de les expliciter.
] 29/01/2013
Gérard Duchamp Combinatorial deformations: coloured algebras (tensor products and Lie theory) 22/01/2013
Gérard Duchamp Combinatorial aspects of quantum physicsabstract.htmlThis small account aims at presenting a project which deals
with combinatorial aspects of Quantum Mechanics (or
Physics).
] 22/01/2013
Adrian Tanasa Grassmanian variables, Grassmann-Berezin integrals and things we can do withabstract.htmlIn this talk I will introduce Grassmann variables and the basic rules of Grassmann-Berezin calculus. I will then show how we can use these tools to express Pfaffians and determinants and to derive various non-trivial identities in combinatorics and combinatorial physics (deletion/contraction relation for graph polynomial, Desnanot-Jacobi identities etc.).
] 22/01/2013
Journées du GDR-IM (21-22 janvier)15/01/2013
Philippe Marchal Génération aléatoire de permutations alternéesabstract.htmlDésiré André (dans son article de 1879) a montré que le développement en série de tan(x) et sec(x) est lié à une jolie suite combinatoire,
les nombres Eulériens, qui comptent le nombre de permutations alternées.
J'introduis un nouvel algorithme, basé sur des idées de théorie des probabilités,
qui permet d'engendrer une telle permutation de longueur n en temps n log n.
Je montrerai que l'idée peut aussi s'étendre à d'autres classes de permutations contraintes.
] 15/01/2013
Nguyên Hoàng Nghĩa The Tutte polynomial for matroids, a renormalization group-like approachabstract.htmlUsing a quantum field theory renormalization group-like differential equation, we give a new proof of the recipe theorem for the Tutte polynomial for matroids. The solution of such an equation is in fact given by some appropriate characters of the Hopf algebra of isomorphic classes of matroids, characters which are then related to the Tutte polynomial for matroids.
] 08/01/2013
Hoang Ngoc Minh Polyzêtas colorés 18/12/2012
Christophe Tollu Théorie des modèles : une application 04/12/2012
Stephen Melczer A classification of restricted lattice walks with small steps [Slides.pdf ]abstract.htmlThe enumeration of lattice walks in restricted regions is an elegant problem which has been the subject of much attention. In this talk we survey recent results
on lattice walks in the quarter plane, regarding the analytic properties of their generating functions. Specifically, we discuss the classification of walks
whose generating functions satisfy linear differential equations, and why this property is desirable.
] 04/12/2012
Laurent Poinsot Classes combinatoires : un point de vue catégorique [Slides.pdf ] 27/11/2012
Stéphane Dartois Développements asymptotiques pour les modèles tensoriels 20/11/2012
Thomas Fernique Pavages de Penrose revisitésabstract.htmlDans les années 70, Ammann et Penrose ont indépendamment découvert
deux losanges légèrement déformés qui permettent de paver le plan
(c'est-à-dire de le couvrir en entier sans que les losanges ne se
superposent), mais seulement de façon non-périodique. De Bruijn a par
la suite montré que ces pavages pouvaient être vus comme des
discrétisations d'un plan totalement irrationnel de l'espace euclidien
à cinq dimensions.
Nous montrerons comment, dans cet espace, les déformations de ces
losanges se traduisent en contraintes géométriques simples qui
permettent de retrouver le résultat de De Bruijn par une méthode
différente, plus générique. Pour illustrer cette généricité, nous
présenterons une variante des losanges de Ammann et Penrose dont les
pavages peuvent être vus comme des discrétisations d'une famille à
deux paramètres de plans de l'espace euclidien à cinq dimensions.
Il s'agit d'un travail en commun avec Nicolas Bédaride (LATP, Marseille).
] 20/11/2012
Hoang Ngoc Minh Déformations et perturbations du produit de mélange 13/11/2012
Nick Beaton Self-avoiding walks and polygon modelsabstract.htmlIn their recent paper proving the connective constant mu of
self-avoiding walks (SAWs) on the hexagonal (honeycomb) lattice,
Duminil-Copin and Smirnov consider the generating function of
self-avoiding
bridges which span a strip of width T, and conjecture that this
generating function vanishes at 1/mu in the large T limit. This
generating function was again considered by Bousquet-Mélou, de Gier,
Duminil-Copin, Guttmann and myself when we studied the adsorption of
SAWs
onto an impenetrable surface, and we proved the conjecture of
Duminil-Copin
and Smirnov. I will discuss this conjecture and its proof, as well as
what
happens after rotating the lattice by pi/4.
http://arxiv.org/abs/1109.0358 http://arxiv.org/abs/1210.0274
] 13/11/2012
Matthieu Deneufchâtel Sur une famille de bigèbres combinatoires [Slides.pdf ] 12/11/2012
Adrian Tanasa Soutenance d'HDR : "Combinatoire en théories quantiques des champs et modèles de tenseurs aléatoires" 06/11/2012
Carine Pivoteau Un pont entre les espèce de structures et la combinatoire analytique (2/2)abstract.htmlLe livre "Analytic Combinatorics" de Flajolet et Sedgewick propose un cadre agréable -- la Méthode Symbolique -- pour définir des classes
d'objets combinatoires à partir de grammaires (systèmes combinatoires) semblables à celles de
la théorie des langages. En se plaçant dans ce cadre, il est possible d'effectuer un certain
nombre de traitements quasi-automatiques sur ces objets : manipulation
de séries génératrices, génération aléatoire, analyse asymptotique, ...
Cependant, lorsqu'il s'agit d'implanter de telles méthodes, il est
nécessaire de se poser la question: comment savoir si un système
combinatoire donné est "bien formé" ?
Cette question nous a amenés à considérer une autre approche
permettant de décrire des objets combinatoires : la théorie des espèces
de structures. Bien qu'étudiées à des fins très différentes, ces deux approches présentent de nombreux
points communs et permettent, lorsqu'elles sont associées, de fournir une base de travail solide
pour l'automatisation d'un certain nombre de traitements combinatoires.
Dans cet exposé, nous présenterons ces deux approches et nous décrirons les passerelles menant de l'une à l'autre, dans le but de
caractériser les systèmes qui décrivent effectivement des structures combinatoires.
Cette présentation est basée sur un travail en commun avec B. Salvy et
M. Soria.
] 06/11/2012
Carine Pivoteau Un pont entre les espèce de structures et la combinatoire analytique (1/2)abstract.htmlLe livre "Analytic Combinatorics" de Flajolet et Sedgewick propose un cadre agréable -- la Méthode Symbolique -- pour définir des classes
d'objets combinatoires à partir de grammaires (systèmes combinatoires) semblables à celles de
la théorie des langages. En se plaçant dans ce cadre, il est possible d'effectuer un certain
nombre de traitements quasi-automatiques sur ces objets : manipulation
de séries génératrices, génération aléatoire, analyse asymptotique, ...
Cependant, lorsqu'il s'agit d'implanter de telles méthodes, il est
nécessaire de se poser la question: comment savoir si un système
combinatoire donné est "bien formé" ?
Cette question nous a amenés à considérer une autre approche
permettant de décrire des objets combinatoires : la théorie des espèces
de structures. Bien qu'étudiées à des fins très différentes, ces deux approches présentent de nombreux
points communs et permettent, lorsqu'elles sont associées, de fournir une base de travail solide
pour l'automatisation d'un certain nombre de traitements combinatoires.
Dans cet exposé, nous présenterons ces deux approches et nous décrirons les passerelles menant de l'une à l'autre, dans le but de
caractériser les systèmes qui décrivent effectivement des structures combinatoires.
Cette présentation est basée sur un travail en commun avec B. Salvy et
M. Soria.
] 23/10/2012
Juanjo Rué Perna On the probability of planarity of a random graph near the critical point [Slides.pdf ]abstract.htmlConsider the uniform random graph G(n,M) with n vertices and M edges.
Erdős and Rényi (1960) conjectured that when n goes to infinity, then the limit
of "Pr(G(n,n/2) is planar" exists and is a constant strictly between 0 and 1. Łuczak, Pittel and Wierman (1994) proved this conjecture
and Janson, Łuczak, Knuth and Pittel (1993) gave lower and upper bounds for this probability.
In this talk we show how to determine the exact probability of a
random graph beingplanar near the critical point M=n/2. More exactly,
for each λ, we find an exact analytic expression for
p(λ) = \lim_{n \to \infty} \Pr{G(n,n/2 (1+λ n^{-1/3})) is planar}.
In particular, we obtain p(0) \approx 0.99780.
If time permits we will show extensions of these techniques and further research.
This is joint work with Marc Noy (UPC-Barcelona) and Vlady Ravelomanana (LIAFA-Paris)
] 23/10/2012
Gérard Duchamp Sweedler's duals and Schützenberger's calculusabstract.htmlThe theoretical setting of his talk is based essentially on the paper - http://hal.archives-ouvertes.fr/hal-00193180/ - published in a workshop about Combinatorial Physics [1].
This setting was used to prove, with Christophe Reutenauer,
a conjecture by Alain Connes [2].
We give new insights and applications of this concept.
] 16/10/2012
Hsien-Kuei Hwang Maxima of multivariate samples: theory, algorithms and applications 16/10/2012
Hoang Ngoc Minh Séries de rang de Lie fini 09/10/2012
Anna Frid Comptage des mots de rotation [Slides.pdf ]abstract.htmlNous donnons une formule précise pour le nombre total des mots de
rotation engendrés par deux intervalles. Le résultat utilise les
travaux de Berstel et Pocchiola sur les mots sturmiens. Il continue
aussi un résultat par Cassaigne et Frid (2007) sur le comptage des
mots de rotation dont l'intervalle est fixé.
[Travail commun avec D. Jamet]
] 09/10/2012
Gérard Duchamp Groupe de Hausdorff et coordonnées localesabstract.htmlIn classical Lie groups, the product of
one-parameter groups wrt any basis of the
tangent Lie algebra provides an open mapping which
gives at once a system of local coordinates.
We discuss the transposition of this process to the
Hausdorff (profinite) Lie group with several combinatorial
alphabets.
] 02/10/2012
Gérard Duchamp Quelques remarques sur les caractères et la renormalisation (travaux en cours) 02/10/2012
Christophe Tollu Sur les corps de fonctions et leurs extensions 27/09/2012
Matthieu Deneufchâtel Soutenance de thèse : Iterated integrals in combinatorial physics [Slides.pdf ] 25/09/2012
Collectif
Inauguration du salon de thé combinatoireabstract.htmlCe "salon de thé combinatoire" avec petits gâteaux et grandes
questions se veut un groupe de
travail libre autour de la combinatoire.
Ce salon est ouvert à tous, chacun pouvant exposer de manière
décontractée ses travaux en cours, ses problèmes ouverts, ses lectures
scientifiques... Nous souhaitons un lieu de partage convivial et
actif. Un lieu où l'on peut lancer des idées, poser des questions
naïves ou profondes sans crainte. En d'autres termes, un lieu où faire
de la recherche !
] 25/09/2012
Bernhard Gittenberger Infinite-dimensional functional equations and Gaussian limiting distributionsabstract.htmlWhat Philippe Flajolet popularized as the "Drmota-Lalley-Woods
theorem" gives
a kind generalisation of the Perron-Frobenius theory (rational world)
to polynomial system of equations (algebraic world).
It establishes a universal behaviour (square singularity, Gaussian
limit law).
This talk will deal with systems of functional equations in finitely
or
infinitely many random variables arising in combinatorial enumeration
problems.
We prove sufficient conditions under which the combinatorial random
variables encoded in the generating function of the system
tend to a finite or infinite dimensional limiting distribution.
The proofs use a pinch of complex analysis and functional analysis.
[Joint work with Michael Drmota and Johannes Morgenbesser]
] 25/09/2012
Vonjy Rasendrahasina Soutenance de thèse : MAX-2-XORSAT 18/09/2012
Michael Drmota Extremal parameters in critical and subcritical graph classes [Slides.pdf ]abstract.htmlIn recent years there has been increasing interest in the asymptotic
analysis of (several classes of) planar maps and planar graphs. This
was initiated by bijective methods (e.g. the Shaeffer bijection),
generating function methods (e.g. Gimenez and Noy's result on the
asymptotics of number of planar graphs) and the search for
probabilistic limiting objects (e.g. the Brownian map by Le Gall). In
particular in the discussion of several planar graph classes (like
series-parallel graphs or labelled planar graphs) a dichotomy between
a "critical" and "subcritical" behaviour between 2-connected and
connected graphs was observed. Informally a graph class is subcritical
when all 2-connected components are small (i.e., at most of log n -
size) and one observes a "treelike structure". Conversely a graph
class is critical when the largest 2-connected component is comparable
to the size of the whole graph.
The purpose of this talk is to discuss the asymptotic behaviour of
several (extremal) parameters of subcritical and critical graph
classes, in particular the diameter and the maximum degree. For
subcritical graph classes the diameter is (usually) of oder n^(1/2)
whereas we can expect the order n^(1/4) in the critial case. On the
other hand the maximum degree is (usually) of order log n in both
cases. However, critical graph classes are notoriously more difficult
to handle than subcritical ones.
This talk is mainly based on joint work with Omer Gimenez, Marc Noy,
Konstantinos Panagiotou, and Angelika Steger.
] 18/09/2012
Matthieu Deneufchâtel Un théorème différentiel [Slides.pdf ]abstract.htmlDans cet exposé, nous présentons un théorème relatif à un critère d'indépendance linéaire des coefficients d'une solution d'une équation différentielle non commutative. Ce théorème a pour conséquence l'indépendance linéaire des polylogarithmes et de leur généralisation, les hyperlogarithmes, sur des corps de fonctions.
Dans la suite nous regardons à travers le miroir pour avoir des renseignements sur les dérivations.
] 03/09/2012
Matthieu Deneufchâtel Iterated integrals in combinatorial physics 03/09/2012
Nguyên Hoàng Nghĩa On the selection/quotient principle 07/08/2012
Collectif
CQMM and rewriting (part 2)abstract.htmlNous devons comprendre les
aspects du théorème de
CQMM préparatoires à l'implémentation.
Cela passe par une phase
d'analyse/conception des différentes réécritures
qui lui sont liées.
] 07/08/2012
Collectif
CQMM and rewriting (part 1)abstract.htmlNous devons comprendre les
aspects du théorème de
CQMM préparatoires à l'implémentation.
Cela passe par une phase
d'analyse/conception des différentes réécritures
qui lui sont liées.
] 31/07/2012
FPSAC 2012 (30 juillet-3 août)31/07/2012
Gérard Duchamp Quelques lois exotiques (et utiles) pour le ξ-stuffle (2/2)abstract.htmlLes constantes de structure (ou coefficients de linéarisation)
de certaines algèbres (comme les fonctions rationnelles nulles à
l'infini) ont une riche combinatoire que nous nous proposons
d'illustrer et de discuter sur quelques exemples.
] 31/07/2012
Matthieu Deneufchâtel Combinatoire des bases en dualité pour différents stuffles 24/07/2012
Gérard Duchamp Quelques lois exotiques (et utiles) pour le ξ-stuffle (1/2)abstract.htmlLes constantes de structure (ou coefficients de linéarisation)
de certaines algèbres (comme les fonctions rationnelles nulles à
l'infini) ont une riche combinatoire que nous nous proposons
d'illustrer et de discuter sur quelques exemples.
] 17/07/2012
Hoang Ngoc Minh Polyzetas irréductibles et bases de Gröbnerabstract.htmlLe passage des polyzêtas de Riemann aux polyzêtas de Hurwitz colorés nécessite une déformation du stuffle au duflle puis au truffle. Dans cet exposé, nous suivons la trace de la déformation de l'algèbre de Hopf en précisant des calculs (et des algorithmes) de base concernant le logarithme, l'exponentielle, la détermination des éléments primitifs et de l'antipode.
] 17/07/2012
Hoang Ngoc Minh Shuffles, duffles, trufflesabstract.htmlLe passage des polyzêtas de Riemann aux polyzêtas de Hurwitz colorés nécessite une déformation du stuffle au duflle puis au truffle. Dans cet exposé, nous suivons la trace de la déformation de l'algèbre de Hopf en précisant des calculs (et des algorithmes) de base concernant le logarithme, l'exponentielle, la détermination des éléments primitifs et de l'antipode.
] 10/07/2012
Olivier Bouillot Les multitangentes, vues à travers les multizêtas de Hurwitz (part 2)abstract.htmlLes multizêtas sont les nombres définis par des sommes itérées sur les entiers strictement positifs, généralisant les valeurs de la fonction ζ de Riemann aux entiers supérieurs à 2. Ceux ci possèdent de nombreuses dénominations dans la littérature : polyzêtas, nombres d'Euler-Zagier, valeurs zêta multiples, sommes harmoniques multiples.... L'étude algébrique et arithmétique de ces nombres pourrait apparaître comme étant du folklore mathématique. Cependant, il n'en est rien : cette étude se trouve justifiée par l'apparition de ces nombres, depuis 30 ans, dans des domaines très variés et très actifs des mathématiques : théorie des nombres, groupes quantiques, diagrammes de Feynman, théorie de la résurgence, ...
] 10/07/2012
Olivier Bouillot Les multitangentes, vues à travers les multizêtas de Hurwitz (part 1)abstract.htmlLes multizêtas sont les nombres définis par des sommes itérées sur les entiers strictement positifs, généralisant les valeurs de la fonction ζ de Riemann aux entiers supérieurs à 2. Ceux ci possèdent de nombreuses dénominations dans la littérature : polyzêtas, nombres d'Euler-Zagier, valeurs zêta multiples, sommes harmoniques multiples.... L'étude algébrique et arithmétique de ces nombres pourrait apparaître comme étant du folklore mathématique. Cependant, il n'en est rien : cette étude se trouve justifiée par l'apparition de ces nombres, depuis 30 ans, dans des domaines très variés et très actifs des mathématiques : théorie des nombres, groupes quantiques, diagrammes de Feynman, théorie de la résurgence, ...
] 03/07/2012
Gérard Duchamp The contrivances of shuffle products and their siblings 26/06/2012
Mario Valencia-Pabon Lokshtanov-Nederlof's exact pseudo-polynomial time algorithm for the knapsack problem in polynomial space 26/06/2012
Gérard Duchamp An interface between physics and number theory 25/06/2012
Omar Ait Mous Soutenance de thèse 19/06/2012
AofA 2012 (17-22 juin)05/06/2012
Daniel Barsky Éléments d'ordre une puissance de p dans le groupe symétrique, exponentielle de Dwork et analyse p -adique d'après Conrad, Ishihara, Ochiai, Takegahara, Yoshidaabstract.htmlLes auteurs suscités ont montré que le nombre de solutions, bn,p
de gp =1 dans le groupe Sn possède d'intéressante propriétés
p -adique. Je montre que ce résultat équivaut à une propriété
(inattendue ?) de prolongement analytique p -adique de la fonction
Gamma p -adique. Ce résultat se généralise.
] 05/06/2012
Pierre-André Picon Produits-quotients de factorielles, fonction partie entière et lien avec le théorème de Tchebycheff et l'hypothèse de Riemann 29/05/2012
Hypergeometric series and algebra, geometry, number theory and physics (29 mai-1 juin, IHP)22/05/2012
Christophe Tollu Catégories, automates et représentations I 22/05/2012
Henning Bruhn-Fujimoto Matroïdes infinisabstract.htmlUn matroïde est une structure sur un ensemble fini qui
généralise au même temps l'indépendance dans un espace vectoriel et le
comportement des arbres couvrant d'un graphe. Parmi les points clés
d'un matroïde sont la dualité et l'existence des bases et des
circuits. En 1966, Rado a demandé comment la définition des matroïdes
se laisse étendre sur des ensembles infinis en gardant ces propriétés
clées. Dans l'exposé je donnerai une réponse à la question de Rado.
Travail en collaboration avec R. Diestel, M. Kriesell. R. Pendavingh
et P. Wollan.
] 22/05/2012
Gérard Duchamp Combinatoire des états cohérents I : états classiques et généralisés 22/05/2012
CANT 2012 School on Combinatorics, Automata and Number Theory (21-25 mai), CIRM15/05/2012
Roberto Bondesan Percolation and lattice algebras in localization problemsabstract.htmlI will discuss geometrical problems arising from the study of
localization using disordered network models. I will focus mostly on
relations to the percolation problem and the role of lattice algebras.
http://arxiv.org/abs/1004.3198v1 : survey de John Cardy sur le sujet
] 15/05/2012
Bernhard Gittenberger Some shape characteristics of Pólya treesabstract.htmlWe discuss the asymptotic behaviour of some typical shape
characteristics like profile and height as well as a refinement like
the degree profile of Pólya trees (unlabeled, nonplane rooted
trees). We prove a local limit theorem for the height and a functional
limit theorem for the profiles.
] 01/05/2012
fête du séminaire
24/04/2012
Gérard Duchamp Composition de fonctions représentatives : shuffles, produits de Cauchy et de Hadamard 24/04/2012
Olivier Roussel Shuffle de langages et génération aléatoire 24/04/2012
Margherita Disertori Matrices aléatoires gaussiennes unitaires et méthodes de point col 24/04/2012
Stéphane Dartois Various combinatorial aspects of tensor models 17/04/2012
Christophe Tollu Initiation à la dualité entre groupes et catégories de représentations (2/2)abstract.htmlLa théorie de la dualité de Tannaka est l'étude des interactions entre un groupe et la catégorie de ses représentations. Les premiers théorèmes de Krein et Tannaka se concentraient sur la question de la reconstruction d'un groupe compact à partir de ses représentations. On présentera quelques constructions catégoriques qui jouent un rôle important dans la présentation moderne de cette théorie "classique".
] 17/04/2012
Gérard Duchamp Mécanique quantique, clôtures rationnelles et fonctions représentatives 10/04/2012
Christophe Tollu Exercices et compléments 10/04/2012
Éric Balandraud Méthode polynomiale et combinatoire additive dans Fp abstract.htmlApres avoir expose les principes de la methode polynomiale, aussi
appelee Combinatorial Nullstellensatz. Nous detaillerons ses
applications en combinatoire additive. Cette methode donne de
nouvelles preuves de resultats classiques, comme le theoreme de
Cauchy-Davenport ou de Erdos-Ginzburg-Ziv, et de nombreux resultats
recents. Certaines de ces applications font appel de maniere
surprenante a des determinants binomiaux issus des travaux de Gessel
et Viennot.
] 10/04/2012
Xavier Goaoc Un point de vue combinatoire sur le théorème de Hellyabstract.htmlLe théorème de Helly énonce que si une famille finie de convexe de R^d est d'intersection vide alors elle contient une sous-famille
d'au plus d+1 membres dont l'intersection est déjà vide. J'illustrerai comment ce résultat classique et certaines
de ses généralisations récentes s'expriment naturellement en termes de combinatoire topologique.
Aucune connaissance préalable en géométrie ou topologie ne sera supposée. Travail commun avec Éric Colin de Verdière (CNRS-ENS) et Grégory Ginot (UPMC-ENS).
] 10/04/2012
Christophe Tollu Initiation à la dualité entre groupes et catégories de représentations (1/2)abstract.htmlLa théorie de la dualité de Tannaka est l'étude des interactions entre un groupe et la catégorie de ses représentations. Les premiers théorèmes de Krein et Tannaka se concentraient sur la question de la reconstruction d'un groupe compact à partir de ses représentations. On présentera quelques constructions catégoriques qui jouent un rôle important dans la présentation moderne de cette théorie "classique".
] 03/04/2012
Manuel Bodirsky Sur une conjecture d'énumération 03/04/2012
Manuel Bodirsky Théorie de Ramsey et un lien récent avec la topologie dynamique [Slides.pdf ] 03/04/2012
Gérard Duchamp Combinatoire des catégories de modules I : Suites de Jordan-Hölder et q -caractéristiques de Frobeniusabstract.htmlOn explique la partie "catégories de modules" avec
de possibles prolongements.
] 27/03/2012
Séminaire SLC (25-28 mars)27/03/2012
Alice Jacquot Algorithme de Rémy et générateur de Boltzmann pour spécifications holonomesabstract.htmlJe présenterai des travaux en cours avec Olivier Bodini et Axel Bacher
sur la génération aléatoire d'arbres décrit par une spécification
holonome. Cette approche nous permet de généraliser l'algorithme de Rémy.
Référence : http://archive.numdam.org/ARCHIVE/ITA/ITA_1985__19_2/ITA_1985__19_2_179_0/ITA_1985__19_2_179_0.pdf : article de Jean-Luc Rémy
] 20/03/2012
Gérard Duchamp Fonctors U , L and T in combinatoricsabstract.htmlMany combinatorial Hopf algebras are positively graded
in finite dimensions. This has a consequence on Hilbert series of
(and in) these. For example, in FQSym , the Hilbert series of the
cocommutative part could be computed and it was conjectured with
some evidence that the primitive part was a free lie algebra.
We give some hints on an ongoing work.
] 20/03/2012
Mark Ward A solved problem in analysis. An unsolved problem in analysis. 20/03/2012
Tanguy Rivoal Quelques propriétés analytiques des applications miroir 20/03/2012
Christophe Tollu Combinatoire des représentations polynomiales des groupes généraux linéaires 13/03/2012
Loïk Lhote Complexité moyenne de la recherche de motifs fréquents et de traverses minimales d'hypergraphes [Slides.pdf ]abstract.htmlLa fouille de données est le domaine qui vise à extraire automatiquement
de l'information dans de grandes masses de données. Une manière de faire
est d'extraire des motifs qui vont contenir cette information et qui
servent
ensuite à créer des règles d'association. Il existe un grand nombre de
motifs
(motifs fréquents, fermés, libres, émergents, satisfaisant des mesures
d'intérêts, bordure négative, etc.) et une large famille d'algorithmes
dédiés
pour les extraire.
Dans le pire des cas, le nombre de motifs est souvent exponentiel et c'est
souvent la seule information dont on dispose sur la complexité des
problèmes
et des algorithmes. Pourtant en pratique, les algorithmes sont efficaces
lorsqu'ils sont utilisés avec des paramètres raisonnables. L'analyse
en moyenne
qui, contrairement à celle dans le pire des cas, tient compte de toutes les
entrées possibles peut expliquer ce genre de phénomène.
L'exposé présentera des analyses en moyenne concernant les motifs
fréquents et les traverses minimales d'hypergraphes. Le calcul des
traverses
minimales est fondamental en fouille de données puisqu'il existe par
exemple
une bijection avec les motifs de la bordure négative. Une question
algorithmique
encore ouverte est de savoir si le calcul des traverses minimales est
output-polynomial (polynomial en la taille de l'entrée plus celle de
la sortie) dans
le pire des cas. Un éclairage en moyenne sera apporté à cette question.
] 13/03/2012
Arnaud Mary Génération des dominants minimaux d'un graphe [Slides.pdf ]abstract.htmlLa théorie des bases de données et la théorie des treillis présentent
de nombreux liens que je rappellerai dans cette présentation. Je
présenterai ensuite le problème de génération des transversaux
minimaux d'un hypergraphe et j'expliquerai en quoi celui-ci est
fortement lié à la théorie des treillis. Un hypergraphe H est une
collection d'ensembles E (appelés hyperarête) sur un ensemble de
sommet V. Un transversal de H est un ensemble de sommets qui intersecte
toutes les hyperarêtes de H. Le problème de génération associé au
transversaux, consiste à "lister" tous les transversaux minimaux d'un
hypergraphe, c'est-à-dire ceux qui ne contiennent aucun autre
transversal.
Je parlerai enfin d'un cas particulier du problème de génération des
transversaux minimaux qui est la génération des dominants minimaux
d'un graphe.
] 13/03/2012
Christophe Tollu Combinatoire fine des représentations des groupes symétriques et linéaires 06/03/2012
Journées Aléa (4-9 mars)06/03/2012
Gérard Duchamp Les mécanismes de perturbation du shuffle (théorèmes de structure)abstract.htmlLorsque la structure tensorielle n'est pas déformée, on a
tout un univers de déformations du shuffle par addition d'un terme
de type Hofmann. Lorsque le coproduit associé à ce terme est dualisable,
on obtient des bigèbres. On examine ici les théorèmes fondamentaux qui
gouvernent les structures de ces bigèbres (travail en cours).
Si le temps le permet, la séance sera suivie d'un entrainement au calcul
tensoriel.
] 06/03/2012
Gérard Duchamp Quantum and Hopf : FQSym and a question of C. Reutenauerabstract.htmlWe tell the story of FQSym and its link to Combinatorial Physics through
FQSymq and MQSym .
] 28/02/2012
Viviane Pons Les bases de l'anneau des polynômes en Sageabstract.htmlL'anneau des polynômes en n variables est souvent vu de façon récursive
comme l'anneau des polynômes en 1 variable à coefficients dans les
polynômes à n-1 variables. Nous montrons une approche différente qui étudie
l'anneau comme une somme linéaire de vecteurs d'entiers de taille n : les
exposants des monômes. A partir d'opérations simples sur les vecteurs, on
obtient des actions sur les polynômes. Nous définissons des opérations de
différences divisées à partir desquelles nous obtenons des bases linéaires
de l'anneau des polynômes. Ces bases apparaissent dans le contexte de la
géométrie algébrique et peuvent être vues comme des généralisations de
certaines bases des polynômes symétriques. Tout l'exposé sera illustré de
calculs effectués à partir du logiciel Sage.
] 28/02/2012
Pavel Salimov Open problems on maximal pattern complexity of infinite wordsabstract.htmlA pattern T={t_0 < t_1 <...} is a containing 0 finite subset of N. A pattern
complexity p_x(T) of an infinite word x: N->{0,1} on pattern T is a number
of different words of the form x_{t_0}x_{t_1}...
Maximal pattern complexity of x is the function
p_x(n) = sup_{|T|=n} p_x(T) of n that takes a maximal value of all pattern complexities
of x over patterns of cardinality n.
In the talk, I'll describe some properies of this function, compare it to
the other well-studied measures of complexity, give an example of
calculating it and outline some open problems related to it.
] 28/02/2012
Gérard Duchamp Matrices tassées et convolutionabstract.htmlOn rappelle la construction des algèbres de Hopf MQSym et LDiag, puis on étudie le groupe de Lie du voisinage de l'unité pour la convolution dans ces algèbres. Une démonstration explicite du théorème de Cartier-Quillen-Milnor-Moore à l'aide de ce groupe de Lie est possible en général, elle est donnée et on tente de dégager les premiers éléments de combinatoire qui en découlent pour ces algèbres de Hopf.
] 27/02/2012
Rencontre "Combinatorics of Mathematical Renormalization" 21/02/2012
Algorithms and Permutations (20-21 février)21/02/2012
Gérard Duchamp Ordered infinite products in analysis and combinatorial applications (3/3)abstract.htmlWe continue our exploration of the combinatorics of groups. k[G] is
the full function space kG .
In many cases, given a function φ∈ kG , there exists
no nice formula for φ(fg) . (fg) can be nicely split. Examples will be taken in :
Faà di Bruno formula, Free group, Noncommutative
Symmetric function. If time permits, we will treat some points
of the theory of deformation and some combinatorial aspects
of quantum groups.
] 14/02/2012
Alain Plagne Quelques exos de théorie additive des nombres 14/02/2012
Alain Plagne Une introduction aux aspects combinatoires de la théorie additive des nombres 14/02/2012
Hoang Ngoc Minh 14/02/2012
Gérard Duchamp Ordered infinite products in analysis and combinatorial applications (2/3)abstract.htmlWe pursue our exploration of infinite products by
examples of complete monoidal factorizations and
applications to "Lie" groups which are classic
in combinatorics (Riordan, Haussdorff). We
construct the Faà di Bruno Hopf algebra
through a very simple specialization of the
exponential formula. This talk is meant to be
a partial contribution to F4M sessions.
] 07/02/2012
Mathieu Feuillet Comportement transitoire des processus d'Ehrenfest et d'Engsetabstract.html Nous considérons deux processus stochastiques classiques : les urnes
d'Ehrenfest, introduites en 1907 pour la théorie cinétique des gaz
pour décrire les échanges de chaleur entre deux corps et le modèle
d'Engset introduit en 1918 et qui est, avec le modèle d'Erlang, un des
tous premiers modèles stochastiques de réseaux de communication. Nous
proposons d'étudier le comportement asymptotique de la distribution
des temps d'atteinte de ces deux processus lorsque le nombre de
particules ou d'utilisateurs croît vers l'infini. En particulier, nous
obtenons des résultats sur les temps d'atteinte de frontière. Cette
étude repose sur des techniques de martingales et notamment sur une
famille de martingales positives qui est l'équivalent pour le
processus d'Ehrenfest des martingales exponentielles utilisées pour
l'étude des marches aléatoires et du mouvement brownien.
] 07/02/2012
Basile Morcrette Urnes de Pólya : le miracle de la résolution par combinatoire analytique [Slides.pdf ]abstract.htmlLes modèles d'urnes de Pólya sont des objets très simples mais pour lesquels de nombreuses questions restent ouvertes. Depuis 2005, une approche utilisant la
combinatoire analytique s'est développée (Flajolet-Gabarro-Pekari, puis Flajolet-Dumas-Puyhaubert). Nous verrons, à travers des exemples concrets, comment la
combinatoire analytique permet d'appréhender ces modèles. Les exemples proposés proviendront des fonctions booléennes, des k-arbres, ainsi que des modèles de
croissance de population.
] 07/02/2012
Gérard Duchamp Ordered infinite products in analysis and combinatorial applications (The end of mathematical theories?) (1/3)abstract.htmlWe explore the notions of summability and
multipliability as they are developed classically
in analysis.
We give examples in combinatorics where
infinite products are supplied and, using the
concept of https://www.encyclopediaofmath.org/index.php/Generalized_sequence
we give a rigorous framework for these products.
Also a contribution to F4M via the exponential formula.
] 31/01/2012
Harald Andrés Helfgott Lattice dimers : asymptoticsabstract.htmlSoit R une région finie dans le plan carrelé, il y a un nombre fini de
manières de la recouvrir avec des dominos. Choisissons un recouvrement au
hasard de manière uniforme. Quelle est la probabilité de trouver une
configuration donnée dans un endroit donné ?
Dans le contexte de problèmes de recouvrement, les deux régions plates
finies les plus étudiées sont probablement le rectangle (depuis Kasteleyn
(1961)) et le diamant aztèque (Elkies, Kuperberg, Larsen et Propp (1992)).
Ces deux cas illustrent deux extrêmes de comportement asymptotique.
Les probabilités des configurations locales dans un rectangle ont été
déterminées par Kenyon (1997). Nous verrons comme déterminer de manière
exacte les probabilités des configurations locales dans un diamant
aztèque, avec une esquisse des asymptotiques. Les résultats (et leurs
preuves!) sont nettement différents de ceux du cas rectangulaire.
] 31/01/2012
Harald Andrés Helfgott Lattice dimers : enumerationabstract.htmlSoit R une région finie dans le plan carrelé, il y a un nombre fini de
manières de la recouvrir avec des dominos. Choisissons un recouvrement au
hasard de manière uniforme. Quelle est la probabilité de trouver une
configuration donnée dans un endroit donné ?
Dans le contexte de problèmes de recouvrement, les deux régions plates
finies les plus étudiées sont probablement le rectangle (depuis Kasteleyn
(1961)) et le diamant aztèque (Elkies, Kuperberg, Larsen et Propp (1992)).
Ces deux cas illustrent deux extrêmes de comportement asymptotique.
Les probabilités des configurations locales dans un rectangle ont été
déterminées par Kenyon (1997). Nous verrons comme déterminer de manière
exacte les probabilités des configurations locales dans un diamant
aztèque, avec une esquisse des asymptotiques. Les résultats (et leurs
preuves!) sont nettement différents de ceux du cas rectangulaire.
] 31/01/2012
Olivier Bodini Constructeurs de Flajolet 25/01/2012
Journées du GDR-IM (25-26 janvier)24/01/2012
Michel Rigo Combinatoire des jeux, des mots et numération [Slides.pdf ]abstract.htmlDans la première partie de l'exposé, nous présenterons quelques concepts classiques de la théorie des jeux combinatoires : définition d'un jeu, quelques exemples comme
le jeu de Nim, Wythoff ou Chomp!, graphe et noyau d'un jeu, position perdante/gagnante, nim-somme, fonction de Sprague-Grundy et somme de jeux, etc.
Ensuite, nous montrerons à travers le "célèbre" jeu de Wythoff, variante du jeu de Nim, des liens existant avec la combinatoire des mots. En effet, il est assez facile
de vérifier que le mot de Fibonacci abaababaab..., unique point fixe du morphisme f(a)=ab et f(b)=a, code exactement les positions perdantes du jeu de Wythoff. En
outre, des liens entre les mots substitutifs engendrés par morphisme itéré et les systèmes de numération sont bien connus (la voie a été ouverte par Cobham dans son
papier de 1972 sur les suites k-automatiques). Ainsi, on peut aussi caractériser les positions perdantes du jeux de Wythoff à l'aide de la numération de Zeckendorf
construite sur la suite de Fibonacci 1,2,3,5,8,... Cette caractérisation repose sur des propriétés syntaxiques (testables par automate fini) des représentations dans
ce système.
Partant de ces constatations, nous présenterons, dans la dernière partie de l'exposé, quelques travaux récents montrant les interactions "fructueuses" existant entre
jeux combinatoires, mots infinis engendrés par morphisme et systèmes de numération associés. Nous évoquerons les questions suivantes : étant donné un mot infini comme
le mot de Tribonacci point fixe du morphisme f(a)=ab, f(b)=ac, f(c)=a, peut-on définir un jeu dont les positions perdantes sont codées par ce mot ? Existe-t-il des
variantes du jeu de Wythoff (on change l'ensemble des coups admissibles à jouer) possédant le même ensemble de positions perdantes ? Toute suite de Beatty homogène
donne-t-elle naissance à un jeu combinatoire invariant pour lequel l'ensemble des coups disponibles ne dépend pas de la position de jeu ?
Quelques références :
A. Fraenkel, Heap Games, Numeration Systems and Sequences, Annals of Combin.. 2 (1998), 197–210.
http://www.discmath.ulg.ac.be/publi.html
pour une référence "grand public" sur les jeux combinatoires, voir par exemple les notes :
Enfin, pour un survol sur les numérations (avec quelques remarques sur les jeux combinatoires), cf.
M. Rigo, Numeration Systems: a Link between Number Theory and Formal Language Theory, Proceedings of Developments in Language Theory, London, Ontario, Canada (2010),
Lect. Notes in Comput. Sci. 6224, 33-53 Springer-Verlag (2010), http://orbi.ulg.ac.be/handle/2268/35488
] 24/01/2012
Gérard Duchamp Physique combinatoire : chemins, diagrammes de Ferrers et matrices de transfertabstract.htmlOn part d'un opérateur montant
M et d'un opérateur descendant
D et
on étudie le problème physique du
"paquet de transfert" (l'ensemble des histoires qui mènent
d'un niveau
n au niveau
n+k ).
La série génératrice de toutes ces histoires est un langage sur l'alphabet
{M,D} qui se spécialise en des fractions continues doubles.
D'autre part, l'histoire des réécritures d'une chaîne en
M et
D se retrouve
dans les statistiques de placements de tours (rook numbers) sur des diagrammes
de Ferrers qui donne très simplement les constantes de structures de HW.
Ceci conduit aux HW-graphes et à leurs couplages qui à leur tour peuvent être
déduits de la trace des calculs sur un centre infiniment engendré.
Voir:
Combinatorial Models of Creation-Annihilation
Pawel Blasiak, Philippe Flajolet [http://arxiv.org/abs/1010.0354]
Combinatorial Algebra for second-quantized Quantum Theory
P. Blasiak, G. H. E. Duchamp, A. I. Solomon, A. Horzela, K. A. Penson [http://arxiv.org/abs/1001.4964]
] 17/01/2012
Gérard Duchamp Exercices, exemples et preuves 17/01/2012
Axel Bacher Chemins et animaux : applications de la théorie des empilements de piècesabstract.htmlLe but de cet exposé est d'établir des résultats énumératifs sur certaines classes de chemins et d'animaux. Ces résultats sont obtenus en appliquant la théorie des empilements de pièces développée par Viennot. Nous étudions les excursions discrètes (ou chemins de Dyck généralisés) de hauteur bornée ; nous obtenons des résultats énumératifs qui interprètent combinatoirement et étendent des résultats de Banderier, Flajolet et Bousquet-Mélou. Nous décrivons et énumérons plusieurs classes de chemins auto-évitants, dits chemins faiblement dirigés. Ces chemins sont plus nombreux que les chemins prudents qui forment la classe naturelle la plus grande jusqu'alors. Nous calculons le périmètre de site moyen des animaux dirigés, prouvant des conjectures de Conway et Le Borgne. Enfin, nous obtenons des résultats nouveaux sur l'énumération des animaux de Klarner et les animaux multi-dirigés de Bousquet-Mélou et Rechnitzer.
] 17/01/2012
Gérard Duchamp Foncteurs, constructeurs, grammaires, espèces et opérades : que proposer ? (atelier) 10/01/2012
Hanane Tafat Bouzid Sur la diversité des lois limites d'expressions régulières 10/01/2012
Lucas Gerin Distances en percolation et TASEPabstract.html La percolation de paramètre p, c'est ce qui reste dans Z² quand on efface chaque arête indépendamment avec probabilité 1-p.
Quand p est proche de un, il y a une composante connexe infinie. Le TASEP, ce sont des voitures qui avancent de façon aléatoire sur une seule voie, sans se doubler et sans se rentrer dedans. A priori, ça n'a rien à voir.
] 10/01/2012
Charles Delorme Graphes distance-réguliers et partitions équitables [Slides.pdf ]abstract.htmlOn sait que les graphes distance-réguliers ou distance-birégulier
se caractérisent par le fait que les distances à n'importe quel sommet
réalisent de partitions équitables.
Pas de panique: les termes mystérieux seront illustrés par des exemples.
Qu'arrive-t-il si on prend les distances à
d'autres sous-ensembles de sommets?
] 10/01/2012
Gérard Duchamp Espaces fonctionnels et analyse harmonique pour la combinatoire 03/01/2012
Gérard Duchamp Fils rouges et programme de l'année 03/01/2012
Nicolas Broutin Recherches partiellement spécifiées dans les arbres multidimensionnels [Slides.pdf ]abstract.htmlNous considérons la recherche d'éléments dans des structures de données multidimensionnelles (quad trees, k-d trees),
en particulier lorsque certaines coordonnées ne
sont pas spécifiées (partial match query). Nous supposons que les données consistent en un ensemble de points uniformes dans le carré unité.
Pour ce modèle, dans une structure contenant n points, Flajolet et Puech ont montré que le nombre de noeuds C_n(U)
à visiter pour répondre à une requête demandant l'ensemble des données dont la première coordonnée est x=U
est tel que E[C_n]\sim κ n
β , où κ et β sont des constantes explicites.
Nous développons une approche basée sur l'analyse des coûts C_n(s) pour des requêtes à x=s fixé.
Nous donnons en particulier des estimations précises de la variance et de la distribution limite
de C_n(s) lorsque n\to\infty.
Nos résultats permettent de décrire un processus limite pour C_n(s) lorsque s varie dans (0,1).
Travail en collaboration avec Ralph Neininger et Henning Sulzbach.
] 03/01/2012
Brigitte Chauvin Chaînes de Markov à mémoire variable et tries des suffixes [Slides.pdf ]abstract.htmlDans un premier temps, on expliquera comment on produit des mots, au
sens d'une source dynamique probabiliste, avec une source ``VLMC''
(Variable Length Markov Chain). Puis, pour une famille de sources VLMC
associées à un ``peigne infini'', on construira le trie des suffixes
correspondant. On trouvera l'asymptotique de sa hauteur et de son
niveau de saturation, qui ne sont pas toujours logarithmiques. On fera
le lien entre ce comportement asymptotique et les propriétés de mélange de la source.
] 20/12/2011
Hanane Tafat Bouzid Sur la diversité des motifs dans les lois limites d'expressions régulières 20/12/2011
Christophe Tollu Partitions virtuelles, z-mesures et groupe symétrique infini (d'après divers auteurs) 20/12/2011
Andrea Sportiello A (completely new & simpler!) proof of Razumov-Strogonov 14/12/2011
Conférence Philippe Flajolet and Analytic Combinatorics (14-16 décembre) 13/12/2011
Donatella Merlini A survey on Riordan arrays [Slides.pdf ]abstract.htmlHistorically, there exist two versions of the Riordan array concept.
The older one (better known as recursive matrix and
introduced by Barnabei, Brini and Nicoletti)
consists of bi-infinite matrices, deals with formal Laurent series
and has been mainly used to study algebraic properties
of such matrices. The more recent version consists of infinite, lower
triangular arrays, deals with formal power series
and has been used to study combinatorial problems.
The name Riordan arrays has been
coined in 1991 by Shapiro, Getu, Woan and Woodson with the aim of defining
a class of infinite lower triangular arrays with
properties analogous to those of the Pascal triangle. This concept has been
successively studied by Sprugnoli
in the context of the computation of combinatorial sums. Some
other important aspects of the theory have been studied later by
Merlini, Sprugnoli and Verri and
the literature about Riordan arrays is vast and still growing.
After describing the classical properties about this concept, in this
talk we present some recent results concerning
Riordan arrays related to binary words avoiding a pattern
p and show that every Riordan array induces
two characteristic combinatorial identities in three parameters n, k,
m in Z which are valid in the bi-infinite realm of recursive
matrices.
] 13/12/2011
Mireille Bousquet-Mélou Sur le profil des arbres plongésabstract.htmlConsidérons un arbre binaire incomplet : chaque sommet à un fils droit
et/ou un fils gauche.
Attribuons à la racine l'abscisse 0, et au fils gauche (resp. droit)
d'un sommet
d'abscisse i l'abscisse i-1 (resp. i+1), comme il se doit.
On démontre une formule produit simple donnant le nombre d'arbres binaires
ayant n_i sommets d'abscisse i pour tout i.
On la démontre, on l'adapte à d'autres familles d'arbres, et on la
raffine, le tout bijectivement.
Ce travail est réalisé avec Guillaume Chapuy, et motivé par les liens entre
les arbres étiquetés et les cartes d'une part, la mesure ISE d'autre part.
] 13/12/2011
Christophe Tollu Groupe unitaire infini et ses caractères 06/12/2011
Luciano Norberto Grippo Forbidden subgraph characterizations of some classes of intersection graphs [Slides.pdf ]abstract.htmlGiven a finite family of non-empty sets F . The
intersection graph of F is obtained by representing each
set by a vertex, two vertices being adjacent if and only if their
corresponding sets intersect. In this talk we will focus on two
important intersection graph classes, namely circular-arc graphs
(intersection graphs of arc on a circle) and circle graphs
(intersection graphs of chords on a circle). We will present some
partial characterizations by forbidden induced subgraphs for these
classes. Let F be a family of graphs. A graph $G$ is said
to be a probe--F graph if its vertex set can be partitioned
into two sets: a set P of probe vertices and a stable set N of
non-probe vertices in such a way that edges, whose endpoints belongs
to N , can be added to G so that the resulting graph belongs to
F . We will present some forbidden induced subgraphs
characterizations for probe interval graphs and probe unit interval
graphs on superclasses of cographs. Finally, we will present a
complete forbidden induced subgraphs characterization of probe block
graphs.
This talk is based on a mix of joint works with F. Bonomo, G. Durán
and M. Safe.
] 06/12/2011
Christian Lavault & Hoang Ngoc Minh & Gérard Duchamp Quelques propriétés du shuffle 29/11/2011
Christian Lavault & Hoang Ngoc Minh & Cyril Banderier & Hanane Tafat Exercice sur l'identité shuffle de Minh-Petitot 29/11/2011
Daniel Posner Efficient solutions for the λ-coloring problem on classes of graphs [Slides.pdf ]abstract.htmlA λ-coloring of a graph is a function that assigns
frequencies (represented by natural numbers) to its vertices in such
way that if two vertices are adjacent, then their frequencies differ
by at least two, and if two vertices share a common neighbor, then
their frequencies must be different. Motivated by mobile wireless
networks, the λ-coloring problem aims to use the minimum
frequency spectrum without interferences, i.e., respecting the
distances restrictions. It is known that the decision version of this
problem is NP-complete even for simple classes of graphs
such as bipartite graphs, split graphs, and planar graphs.
In this seminar we talk about recent results in $lambda$-coloring,
including efficient solution when it is restricted to the classes of
split permutation graphs and (q, q-4 )-graphs, q fixed.
Joint work with Marcia R. Cerioli.
] 29/11/2011
Christophe Tollu Permutations aléatoires (infinies), partitions aléatoires (infinies) et motivations via la théorie des représentations 22/11/2011
Journée Renormalisabilité en gravité quantique : aspects combinatoires, algébriques et analytiques à l'IHP 15/11/2011
Ladji Kane Shuffles et stuffles 15/11/2011
Robert Cori Quelques problèmes combinatoires inspirés par le modèle physique du tas de sableabstract.htmlCet exposé se veut introductif et élémentaire. Je présenterai la version combinatoire du modèle physique du tas de sable comme un jeu consistant à déplacer des jetons sur les sommets d'un graphe connexe.
J'introduirai et je donnerai les propriétés des configurations récurrentes de jetons, puis les bijections entre ces configurations et les arbres recouvrants du graphe. Une incursion dans les polynômes de Tutte est ensuite prévue, puis une investigation sur les algorithmes de tirage aléatoire d'arbres recouvrants.
Après avoir rappelé ce panorama de travaux remontant aux années 1990-2000, quelques résultats dans des directions nouvelles seront évoqués.
Quelques articles introductifs :
Deepak Dhar (1999)
Dominique Rossin et Robert Cori
Chip-Firing and Rotor-Routing on Directed Graphs
] 15/11/2011
Gérard Duchamp & Hoang Ngoc Minh Déformations et perturbations, des nouvelles des polyzêtas 09/11/2011
Flavia Bonomo On the b-coloring problemabstract.htmlA b-coloring of a graph is a coloring such that every color class
admits a vertex adjacent to at least one vertex receiving each of the
colors not assigned to it. The b-chromatic number of a graph G is the
maximum number t such that G admits a b-coloring with t colors.Several
problems related to b-coloring of graphs have been introduced in the
literature. Recently, the theory of b-colorings of graphs has been
applied in to some clustering problems in data mining processes. In
this talk, we will summarize the last algorithmic and theoretical
results obtained on b-coloring and the related notions of
b-perfection, b-continuity and b-monotonicity within some graph
classes.
This is a mix of joint works with C. Betancur, G. Duran, I. Koch, F.
Maffray, J. Marenco and M. Valencia-Pabon.
] 08/11/2011
Dominique Manchon Deux algèbres de Hopf définies à partir de découpages de graphes 08/11/2011
Patrick Dehornoy Sur la distance de rotation entre deux arbres binaires [Slides.pdf ]abstract.htmlLe problème est de construire des arbres binaires éloignés vis-à-vis
de la distance de rotation, ce qui équivaut à construire des
expressions parenthésées éloignées vis-à-vis de l'associativité, ou
encore des triangulations de polygone éloignées vis-a-vis de l'échange
de diagonales. On présentera la magnifique solution de
Sleator-Tarjan-Thurston basée sur la géométrie hyperbolique, qui est
optimale mais valable seulement pour une taille assez grande (non
effective), ainsi qu'une méthode combinatoire basée sur une notion de
séparatrice dans les associaèdres, qui est (pour le moment) non
optimale, mais valable pour toute taille.
] 08/11/2011
Laurent Poinsot Soutenance d'HDR : Contributions à l'algèbre, à l'analyse et à la combinatoire des endomorphismes sur les espaces de séries [Slides.pdf ]abstract.htmlLe dual topologique de l'espace des séries en un nombre quelconque,
éventuellement infini, de variables non commutatives avec un corps
topologique séparé de coefficients, pour la topologie produit, n'est autre
que l'espace des polynômes. Il en résulte de façon immédiate que les
endomorphismes continus sur les séries sont exactement les matrices infinies
mais finies en ligne. Les matrices triangulaires infinies, puisque formant
une algèbre de Fréchet, disposent quant à elles d'un calcul intégral et
différentiel, que nous développons dans un cadre assez général, et qui
permet d'établir une correspondance exponentielle-logarithme de type Lie.
Nous déployons ces outils sur l'algèbre de Weyl (à deux générateurs)
réalisée fidèlement comme une algèbre d'opérateurs agissant continûment sur
l'espace des séries formelles (en une variable). Puis nous démontrons que
chaque endomorphisme d'un espace vectoriel de dimension infinie dénombrable
peut s'obtenir explicitement sous la forme de la somme d'une famille
sommable en des opérateurs plus élémentaires, les opérateur d'échelle
(généralisation de l'algèbre de Weyl), précisant de la sorte le théorème de
densité de Jacobson. Par dualité (topologique) un résultat similaire
concernant les opérateurs continus sur un espace de combinaisons linéaires
infinies tombent presque gratuitement. Par ailleurs nous développons la
notion d'algèbre (réduite) large d'un monoïde à zéro (obtenue par complétion
de l'algèbre réduite) qui nous permet de calculer de nouvelles formules
d'inversion de Möbius ainsi que des séries de Hilbert.
- Le jury : Jacques Alev, Claude Carlet , Frédéric Chapoton, Patrick Dehornoy,
Gérard Duchamp, Loïc Foissy, Dominique Manchon, Frédéric Patras,
Laurent Rigal et Jean-Yves Thibon.
] 25/10/2011
Collectif
séance d'exo (Cédric Boutillier + Jesper Lykke Jacobsen) [Slides.pdf ] 25/10/2011
Jesper Lykke Jacobsen A tree-decomposed transfer matrix for computing exact Potts model partition functions for arbitrary graphs, with applications to planar graph colouringsabstract.htmlvoir article ArXiV http://fr.arxiv.org/abs/1003.4847
] 25/10/2011
Cédric Boutillier Formalisme d'opérateurs vertex pour l'étude des grandes partitions planesabstract.htmlOn introduira le formalisme utilisé par Okounkov et Reshetikhin pour
étudier les partitions planes aléatoires, basé sur une représentation de
gl(∞). Après avoir expliqué comment calculer avec ce formalisme les
statistiques locales pour ces objets, on présentera le phénomène de
forme limite déterministe lorsque la taille de ces objets tend vers
l'infini. On discutera en particulier l'influence de la forme du « mur
du fond » sur lequel s'appuie la partition plane sur ces propriétés
statistiques. Travail en collaboration avec S. Mkrtchyan, N.
Reshetikhin et P. Tingley.
Références :
A. Okounkov and N. Reshetikhin, Correlation function of Schur process
with application to local geometry of a random 3-dimensional Young
diagram math.CO/0107056, J. Amer. Math. Soc. 16 (2003), no. 3, 581–603.
notre article : arxiv.org/pdf/0912.3968
] 18/10/2011
Collectif
Séance d'exo (Christiane Frougny) 18/10/2011
Christiane Frougny Sur l'addition en parallèleabstract.htmlIl est bien connu que l'addition dans un système de numération
standard a une complexité linéaire, ce qui est trop lent pour faire un
processeur arithmétique efficace. En 1961, Avizienis a donné un
algorithme parallèle d'addition en base 10 avec les chiffres {-6, -5,
..., 5, 6} où la retenue ne se propage pas. On obtient ainsi une
complexité (en parallèle) constante. Dans le langage de la dynamique
symbolique, une telle addition est une fonction locale (sliding block
code). Cette technique est utilisée pour accélérer les algorithmes de
multiplication et de division.
Dans ce travail nous nous intéressons à des systèmes de numération où
la base est un nombre algébrique beta, |beta|>1. Quand tous les
conjugués algébriques de beta ont un module différent de 1, on peut
trouver un alphabet symétrique de chiffres signés entiers sur lequel
faire l'addition en parallèle. Cet algorithme est une généralisation
de celui d'Avizienis.
L'algorithme d'addition est simple, mais l'alphabet obtenu est en
général plus grand que nécessaire. Nous donnons des bornes inférieures
sur la cardinalité minimale d'un alphabet permettant de faire
l'addition en parallèle. Nous présentons ensuite une série de cas où
la borne est atteinte.
Travail en collaboration avec Edita Pelantová et Milena Svobodová
(CTU, Prague)
] 18/10/2011
Matthieu Deneufchâtel Factorisation de Schützenberger, structures libres combinatoires et bases duales [Slides.pdf ]abstract.htmlCet exposé a pour but de présenter la factorisation de Schützenberger dans un cadre général. Nous présentons un théorème général qui permet de l'écrire dans le cas d'une algèbre de Lie quelconque et rappelons les outils nécessaires à sa formulation dans le cadre des structures partiellement commutatives. Nous terminerons en donnant quelques idées concernant des travaux en cours relatifs à l'aller-retour entre bases de PBW et de Radford.
] 11/10/2011
Collectif
séance d'exo (Valérie Berthé) 11/10/2011
Valérie Berthé Substitutions et transcendance [Slides.pdf ]abstract.htmlLes substitutions (c'est-à-dire les morphismes de monoïde libre)
engendrent des mots infinis qui peuvent être vus comme des
développements soit de réels, soit de séries formelles de Laurent
dans des corps algébriques.
Dans le cas de substitutions de longueur constante (suites
automatiques),
les séries ainsi produites sont algébriques. Dans le cas des réels, on
obtient
en général des nombres transcendants. Après une première partie de
survol autour de
ces divers types de comportements algébriques, nous nous
intéresserons aux développements dits S-adiques,
où il ne s'agit plus d'itérer la même substitution, mais de
composer un nombre fini de substitutions.
] 11/10/2011
Miguel Mendez Combinatorial differential equations and shift-plethysm [Slides.pdf ]abstract.htmlThe combinatorial solution to an autonomous differential equation
y´=φ(y) was shown to be the family of increasing φ -enriched
trees (Leroux-Viennot). We introduce a generalization of this kind of
differential equations that uses the operation of shift-plethysm
instead of usual substitution. Its solution is again a family
of φ -enriched trees with labels that give information related
to the length of each branch.
] 04/10/2011
Thomas Fernique Quasicristaux : structure et croissanceabstract.htmlLes quasicristaux sont des matériaux ordonnés, à l'instar des cristaux
habituels, mais sans être périodiques contrairement à ces derniers.
Découverts en 1982 et "officialisés" après 10 ans de controverses, ils
ont contribué à relancer l'étude des pavages non périodiques, qui en
sont un modèle répandu. Dans cet exposé, on s'intéresse à deux
problèmes théoriques principaux de ce modèle : d'une part la
caractérisation de pavages non périodiques par des contraintes locales
(structure des quasicristaux), d'autre part la recherche et l'étude
d'un méchanisme de formation de ces pavages qui soit physiquement
plausible (croissance des quasicristaux). On donnera quelques
résultats marquants ainsi que quelques pistes à explorer.
] 04/10/2011
Jean-Paul Allouche Séries de Dirichlet automatiques (ou comment une constante de Flajolet-Martin ne fut pas evaluée) [abstract.pdf ] 04/10/2011
pot de rentrée du séminaire (12h-14h) 04/10/2011
Brigitte Vallée De l'importance de la discipline des sources [Slides.pdf ]abstract.htmlEn algorithmique, on manipule très souvent des mots, notamment dans l'algorithmique du texte ; plus souvent encore, on manipule ce qu'on appelle communément des clés, notamment dans les algorithmes de tri ou de recherche, ou dans les bases de données.
Dans une perspective plus réaliste, il faut vraiment considérer une clé comme une suite finie de symboles, c'est-à-dire comme un mot.
On remplace alors le coût unitaire d'une comparaison entre deux clés par le coût de la comparaison entre deux mots, égal au nombre de symboles comparés.
L'algorithmique générale devient alors de l'algorithmique du texte, et le processus qui produit les mots, appelé source, acquiert alors une grande importance.
] 27/09/2011
Luc Lapointe Jack superpolynomials, clustering properties and the super-Virasoro algebra (3/3) 27/09/2011
Luc Lapointe Jack superpolynomials, clustering properties and the super-Virasoro algebra (2/3) 27/09/2011
Luc Lapointe Jack superpolynomials, clustering properties and the super-Virasoro algebra (1/3)abstract.htmlThe Jack superpolynomials are symmetric polynomials, involving commuting and anticommuting variables, that are orthogonal eigenfunctions
of a certain integrable model known as the supersymmetric Calogero-Moser-Sutherland model. k , that is, they vanish when k+1 variables are equal but not (conjecturally) when only k are
identified (a sort of generalization of the Pauli exclusion principle).
] 20/09/2011
Séminaire SLC (18-21 septembre)08/09/2011
Exposés-présentation générale des 5 équipes du LIPN 19/07/2011
Apostol Vourdas Harmonic Analysis on some direct and inverse limits 19/07/2011
Christophe Tollu Autour du "Ring Theorem", (d'après Okunkov, Kerov, Vershik) 12/07/2011
Gérard Duchamp Théorie des automates et renormalisation puis discussion 12/07/2011
Pierre Simonnet Clôtures rationnelles et algorithme de Berry-Sethi 12/07/2011
Christophe Tollu Extrémalité et caractères 05/07/2011
Ahmed Djebbar Histoire(s) des mathématiques arabes 05/07/2011
Guy Louchard The Saddle point method in combinatorics asymptotic analysis: successes and failures (A personal view) [Slides.pdf ] 05/07/2011
Étienne Grandjean Complexité, logique et algorithmes [Slides.pdf ] 05/07/2011
Sidi-Mohamed Sedjelmaci L'algorithme d'Euclide en parallèle [Slides.pdf ] 05/07/2011
Wojciech Szpankowski Shannon legacy and beyondabstract.htmlInformation is the distinguishing mark of our era, permeating every
facet of our lives. An ability to understand and harness information has
the potential for significant advances. Our current understanding of
information dates back to Claude Shannon's revolutionary work in 1948,
resulting in a general mathematical theory of reliable communication
that formalized the modern digital communication and storage principles,
paved the way for the Internet, DVDs and iPods of today. While
Shannon's information theory has had profound impact, its application
beyond storage and communication poses foundational challenges. The
National Science Foundation has just established a Science & Technology
Center on the Science of Information to meet the new challenges posed by
the rapid advances in networking, biology and knowledge extraction.
Its missions is to develop rigorous principles guiding the extraction,
manipulation, and exchange of information, integrating elements of
space, time, structure, semantics and context. In this talk, after reviewing main results of Shannon,
we then attempt to identify some features of information
encompassing structural, spatio-temporal, and semantic facets of
information. If time allows, we present one new result on a fundamental
lower bound for structural compression and describe a novel algorithm
achieving this lower bound for graphical structures.
] 05/07/2011
Christian Lavault .28/06/2011
Matthieu Deneufchâtel Autour des "objets de Lie" [Slides.pdf ]abstract.htmlDans cet exposé, je rappelle les définitions de différents objets apparentés par leur nom et que l'on peut ranger dans la classe des "objets de Lie".
J'illustrerai aussi les liens qui les unissent et présente différents théorèmes importants, en particulier dans le mouvement actuel.
Nous parlerons donc, entre autres, d'algèbre de Lie, de groupe de Lie, des théorèmes de Cartier-Quillen-Milnor-Moore et de Poincaré-Birkhoff-Witt.
] 28/06/2011
Gérard Duchamp Lie algebra Prim(H) , CQMM theorem and combinatorial applications 21/06/2011
Ljuben Mutafchiev N-ary subtrees of Galton-Watson trees [abstract.pdf ] 21/06/2011
Adrian Tanasa Hochschild cohomology and combinatorial Dyson-Schwinger equations in quantum field theory [Slides.pdf ]abstract.html I will introduce in this talk the combinatorial Connes-Kreimer Hopf
algebra of Feynman graphs, celebrated structure known to encode the
combinatorics of renormalization in quantum field theory (QFT).
Hochschild cocyles (associated to some particular graphs) will then be
defined; this allows to write down the combinatorial Dyson-Schwinger
equations (recursive equations in power series written in terms of
these Hochschild cocyles). It is worth emphasizing that the
Dyson-Schwinger equations can play a crucial role in non-perturbative
QFTs. Several explicit examples will be given to illustrate these
various notions. Based on: http://arxiv.org/abs/0907.2182
] 21/06/2011
Mathieu Lewin Renormalisation de charge pour un modèle non linéaire issu de l'électrodynamique quantiqueabstract.htmlLa renormalisation est l'un des outils fondamentaux de la théorie
quantique des champs. En particulier, en électrodynamique quantique, on doit
renormaliser la charge et la masse de l'électron.
] 14/06/2011
conférences FPSAC et AofA
07/06/2011
Alan Sokal Higher roots and Hadamard-product formulae [Slides.pdf ] [abstract.pdf ] 07/06/2011
Alan Sokal The leading root of the partial theta-function [Slides.pdf ] [abstract.pdf ] 31/05/2011
Thomas Krajewski Une preuve combinatoire de la formule des équerres de Postnikov [abstract.pdf ] 31/05/2011
Ljuben Mutafchiev On certain statistics of random weighted partitions of large integers [abstract.pdf ] 31/05/2011
Thomas Krajewski Polynômes de graphes et théorie quantique des champs [abstract.pdf ] 24/05/2011
Alan Sokal Applications of the explicit implicit function formula and the exponential formula [Slides.pdf ] [abstract.pdf ] 24/05/2011
Gwendal Collet Cartes avec un nombre fixé de trous [Slides.pdf ] 24/05/2011
Alan Sokal Some wonderful conjectures (but almost no theorems) at the boundary between analysis, combinatorics and probability [Slides.pdf ] [abstract.pdf ] 17/05/2011
Hayat Cheballah Autour de la conjecture de Zeilberger [Slides.pdf ]abstract.htmlOn s'interesse ici a construire une bijection entre deux familles
d'objets combinatoires : les ASMs et les TSSCPPs ou, selon Zeilberger,
entre les triangles Gog et les triangles Magog.
Jusqu'à présent, seule une bijection entre les trapèzes à une ligne
était connue,
et l'étape suivante, celle des trapèzes à deux lignes, semblait
inaccessible. Nous proposons de résoudre ce problème grâce à
l'utilisation d'un outil fondamental en combinatoire, l'involution de
Schutzenberger. Cette construction laisse entrevoir la possibilité
d'une solution complète du problème, en traitant les trapèzes à nombre
arbitraire de lignes.
] 17/05/2011
Valentina Boeva Bioinformatics challenges in next-generation-sequencing era [Slides.pdf ]abstract.html"Next Generation Sequencing" represents a class of relatively new
technologies (first results published in 2007) which enable sequencing
millions of short nucleotide sequences (reads) in several days. I will
briefly discuss several biological applications of "Next Generation Sequencing", such as ChIP-Seq,
transcriptome sequencing, small-RNA sequencing, whole genome sequencing. I
will summarize the main challenges of the primary steps data analysis:
assembly or alignment of reads, normalization of read counts. If I have time
I will also talk about "Next-Next Generation Sequencing" (first results published in 2010).
Références :
http://www.raindancetechnologies.com/documents/Next-Generation-Sequencing_Nature-Genetics_Jan-2010.pdf
Michael L. Metzker (2010) Sequencing technologies : the next generation. Nature Review Genetics
http://fr.wikipedia.org/wiki/Séquençage_de_l'ADN
] 17/05/2011
Muriel Livernet Operades, algebres pre-Lie et algebres de Hopfabstract.htmlOn montrera que l'algebre de Hopf de Connes et Kreimer, apparait de maniere naturelle comme construction d'algebre de Hopf provenant soit de l'operade preLie soit de l'operade NAP, que je definirais. Je donnerai d'autres exemples d'algebres de Hopf qui peuvent etre obtenus a partir de la theorie des operades.
] 10/05/2011
Gérard Duchamp Discussion et exos 10/05/2011
Maxime Crochemore Local repetitions in strings [Slides.pdf ]abstract.htmlThe analysis of repetition in strings constitutes a fundamental
area of combinatorics on words due to important applications to text
algorithms, data compression, music analysis, and biological
sequences analysis, to quote a few.
The talk surveys algorithmic methods used to locate repetitive
segments in strings. It discusses the notion of runs that encompasses
various types of periodicities considered by different authors.
The analysis of related algorithms raises interesting combinatorial
questions and conjectures.
] 10/05/2011
CALIN buffet et violons pour un an de CALIN ! 10/05/2011
Gérard Duchamp et Adrian Tanasa Physique Combinatoire : les trois étages de la fusée 03/05/2011
Vincent Pilaud Le polytope des briques [Slides.pdf ]abstract.htmlL'objet central de cet exposé est le graphe des flips sur les arrangements de pseudodroites avec points de contact couvrant un support donné. Il généralise les graphes
de flips sur trois objets géométriques intéressants : les triangulations d'un polygone convexe, les pseudotriangulations d'un ensemble de points du plan en position
générale, et les multitriangulations d'un polygone convexe. On s'intéresse en particulier à la polytopalité de ces graphes de flips. Par example, le graphe des flips
sur les triangulations est le graphe de l'associahédre et le graphe des flips sur les pseudotriangulations est le graphe du polytope des pseudotriangulations.
Pour les +multitriangulations, la question reste ouverte.
Dans cet exposé, je rappellerai dans un premier temps les principales propriétés combinatoires de ces objets, en soulignant le lien avec les complexes des sous-mots du
groupe symétrique définis par Knutson et Miller. Dans un deuxième temps, je présenterai la construction du "polytope des briques" d'un support. Son graphe est un
sous-graphe du graphe des flips sur les arrangements de pseudodroites ayant ce support. Cette construction contient en particulier toutes les réalisations de
l'associaèdre d'Hohlweg et Lange, qui apparaissent comme polytopes de briques de certains supports bien choisis.
Travail en commun avec Francisco Santos (Université de Cantabrie).
] 26/04/2011
François Delbot Comparaison et évaluation en moyenne d'algorithmes d'approximation pour le problème du vertex coverabstract.html Dans la littérature, on considère souvent qu'un algorithme
d'approximation polynomial est plus performant qu'un autre lorsqu'il possède
un meilleur rapport d'approximation en pire cas. Cependant, il faut être
conscient que cette mesure, désormais "classique", ne prend pas en compte la
réalité de toutes les exécutions possibles d'un algorithme (elle ne
considère que les exécutions menant à la plus mauvaise solution). Dans mes
travaux, je me suis focalisé sur le problème du vertex cover et j'ai tenté
de mieux "capturer" le comportement des ces algorithmes d’approximation en
montrant que les performances moyennes d’un algorithme peuvent être
décorélées des performances en pire cas, en évaluant les performances
moyennes d’un algorithme et en comparant les performances de différents
algorithmes (analytiquement et expérimentalement). J'ai également proposé un
algorithme de liste et j'ai prouvé analytiquement qu'il retourne toujours
une meilleure solution que celle construite par un autre algorithme de liste
récent [ORL 2006] quand ils traitent la même liste de sommets (dans certains
graphes particuliers, la différence de taille peut être arbitrairement
grande). On constate dans ces études que les algorithmes 2-approchés étudiés
sont ceux qui obtiennent les plus mauvaises performances en moyenne et que
ceux qui ont les meilleurs comportements moyens ont de mauvais rapports
d'approximation.
] 26/04/2011
Collectif
Discussions 19/04/2011
Gérard Duchamp Discussion sur les techniques graphiques utilisées en Physique et programme (tentative) 19/04/2011
Wojciech Szpankowski Discrete divide and conquer recurrences [Slides.pdf ]abstract.htmlDivide-and-conquer recurrences are one of the most studied equations in
computer science. Yet, discrete versions of these recurrences
still present some challenges. The discrete nature of this recurrence
(represented by quantization) introduces certain oscillations not
captured by the traditional Master Theorem of divide and conquer
recurrence, for example due to Akra and Bazzi who
primary studied the continuous version of the recurrence.
We show how powerful techniques such as Dirichlet series,
Mellin-Perron formula,
and (extended) Tauberian theorems of Wiener-Ikehara
can be used to provide a complete and precise solution to this basic
computer science
recurrence. We illustrate applicability of our results on several
examples including a popular and fast arithmetic coding algorithm
due to Boncelet for which we estimate its average redundancy and prove
the Central Limit Theorem for the phrase length.
This allows us to compare the redundancy of Boncelet's algorithm to
the (asymptotically) optimal Tunstall scheme.
Join work with M. Drmota (TU Wien)
] 12/04/2011
Razvan Gurau Discussion 12/04/2011
Juan Vera Lizcano Phase transition for the mixing time of Glauber dynamics on regular trees at reconstruction: colorings and independent sets [Slides.pdf ]abstract.htmlGlauber dynamics is a simple Markov chain used to sample (complex) spin
distributions, such as colorings and independent sets, on graphs. We show
that the mixing time of the Glauber dynamics for random k-colorings (and
for the hard core model with boundary conditions) of the complete tree
undergoes a phase transition around the reconstruction threshold. The
central element of our result is a general technique that transforms a
reconstruction algorithm into a set with poor conductance.
] 12/04/2011
Razvan Gurau The 1/N expansion in colored tensor models [Slides.pdf ]abstract.htmlThe 1/N expansion in colored tensor models
] 05/04/2011
Aristide Baratin Aspects of group field theoriesabstract.html"Aspects of group field theories"
] 05/04/2011
Cyril Nicaud Mots de Lyndon aléatoiresabstract.htmlDans cet exposé je présenterai diverses propriétés combinatoires et
algorithmiques des mots de Lyndon aléatoires. Je parlerai principalement
de factorisation standard (travail avec F. Bassino et J. Clément) et
de décomposition en mots de Lyndon. On verra des techniques analytiques
et des techniques probabilistes pour aborder ce genre de questions.
Le résultat principal est que l'on peut décomposer en mots de Lyndon
en temps moyen sous-linéaire. On utilise pour cela une bonne
compréhension de ce qu'est un mot aléatoire "typique" et des
techniques d'algorithmique du texte.
] 05/04/2011
Aristide Baratin Combinatorial state sum invariants from categories [Slides.pdf ]abstract.html"Combinatorial state sum invariants from categories"
] 01/04/2011
Hichem Kenniche Réseaux de capteurs sans fil de grande taille : quelques contributions à la modélisation et à l'algorithmiqueabstract.htmlDate: Wed, 16 Mar 2011 10:29:36
] 29/03/2011
Axel de Goursac Combinatoire algébrique et C* algèbresabstract.htmlAlgebraic structures and C*-algebras
] 29/03/2011
Axel de Goursac Aspect combinatoire de la renormalisation en théorie des champs [Slides.pdf ]abstract.htmlCombinatorial aspects of renormalization in quantum field theory
] 22/03/2011
Flavia Stan A symbolic summation approach to Feynman integral calculus [Slides.pdf ]abstract.htmlWe discuss two methods based on Wilf-Zeilberger summation for the
computation of Feynman parameter integrals.
For the first method, the integrals are rewritten as multisums over
hypergeometric terms to fit the input class of WZ-summation. These
summation problems are highly nested sums with non-standard boundary
conditions. They satisfy inhomogeneous recurrences containing sums of
lower nested depth on the right-hand sides. These last recurrences can be
solved recursively by Carsten Schneider's Sigma package.
Another approach to evaluate Feynman integrals is by representing them as
nested Mellin-Barnes integrals. We show how WZ-methods determine
recurrences for contour integrals of this type, thus eliminating the need
to find sum representations. This algorithmic technique is also applied to
prove typical entries from the Gradshteyn-Ryzhik table of integrals using
the Mellin transform method.
] 22/03/2011
Laura Giambruno Étude de la complexité en états moyenne des opérations rationnelles sur les langages finis [Slides.pdf ]abstract.htmlLa complexité en états d'un langage rationnel est le nombre d'états de
son automate minimal. Dans cet exposé nous considèrerons une
distribution, où les langages finis sont donnés comme une liste de mots, et nous
étudierons la complexité en moyenne des opérations rationnelles: union,
concaténation et étoile.
L'étude en moyenne est particulièrement intéressante quand le pire de
cas est exponentiel, ce qui est le cas ici pour l'étoile et pour la
concaténation. Nous prouverons notamment qu'en moyenne la complexité
est de ces deux opérations est linéaire.
Nous finirons l'exposé en présentant une extension de ces résultats
à d’autres classes de langages. Il s'agit de travaux effectués en collaboration avec F. Bassino et C. Nicaud.
] 22/03/2011
Julien David Génération exhaustive de multiensembles de sous-mots fréquents [Slides.pdf ]abstract.htmlOn étudie le problème suivant: partant d'un mot w et d'un entier q,
on souhaite engendrer toutes les façons possibles de partitionner w en ensemble
de sous-mots fréquents. Un sous-mot est fréquent s'il possède au moins q
occurrences dans la partition. Chaque mot étant associé à un nombre
d'occurrences, on s'intéresse à des multiensembles de mots plutôt qu'à des
ensembles de mots. Par exemple, partant du mot w=cabcba et d'un entier q=2,
le multiensemble {(cb,2),(a,2)} est une solution.
On présentera un algorithme qui engendre l'ensemble des solutions sans
redondance et on montrera que, sauf si P=NP, la complexité de ce problème est
exponentiel dans la taille de la sortie.
On donnera un exemple d'une des applications possibles pour cet algorithme.
] 15/03/2011
Marc Mezzarobba Évaluation numérique de fonctions spéciales et combinatoire analytique avec NumGfun [Slides.pdf ]abstract.htmlL'objet de cet exposé est de présenter NumGfun, un module Maple consacré à la manipulation « analytique » des solutions d'équations
différentielles linéaires à coefficients polynomiaux (fonctions dites D-finies ou holonomes). Les principales fonctionnalités de NumGfun
concernent l'évaluation numérique des fonctions D-finies, et le calcul de bornes qui permettent de contrôler leur comportement. Je ferai une
démonstration de l'utilisation de NumGfun, et je montrerai comment, à travers le calcul certifié de constantes de connection, il peut être
utilisé pour étudier le comportement asymptotique de suites données par des séries génératrices D-finies.
] 15/03/2011
Laurent Boyer Comportements typiques dans les automates cellulaires [Slides.pdf ]abstract.htmlLes automates cellulaires constituent une classe d'objets permettant de
décrire, à l'aide d'une unique règle locale finie, l'évolution,
potentiellement complexe, d'un système infini.
L'objectif de l'exposé est d'introduire un cadre formel permettant de
quantifier des propriétés parmi l'ensemble des automates cellulaires. On commencera par une
présentation de tous les objets considérés. On verra ensuite notre
formalisme proprement dit et ses liens avec la complexité de Kolmogorov. On
évoquera enfin quelques résultats significatifs en s'intéressant d'une part
aux techniques qui interviennent dans nos preuves et d'autre part aux
conséquences de ces résultats sur notre compréhension des automates cellulaires.
] 08/03/2011
Journées Aléa / Séminaire SLC 01/03/2011
Jean-Christophe Novelli Réalisations des algèbres de Hopf combinatoiresabstract.htmlOn illustre l'utilité du concept de réalisation et de spécialisation
d'alphabet d'une algèbre (sur des alphabets commutatifs ou non,
simplement ou
doublement indexés) par une (longue) série d'exemples. Les premiers se
rapportent aux compositions, aux arbres binaires et aux permutations
et on
termine, si le temps le permet, en présentant l'exemple le plus
récent,
celui de l'algèbre de Connes-Kreimer.
] 01/03/2011
Samuele Giraudo Structures algébriques et combinatoires sur les permutations de Baxter [Slides.pdf ]abstract.htmlNous construisons une sous-algèbre de Hopf de l'algèbre de Hopf des
fonctions
quasi-symétriques libres dont les bases sont indexées par les objets
de la
famille combinatoire de Baxter (i.e. permutations de Baxter, couples
d'arbres
binaires jumeaux, etc.). Cette construction repose sur la définition
du
monoïde de Baxter, analogue du monoïde plaxique et du monoïde
sylvestre, et
d'un algorithme d'insertion analogue à l'algorithme de
Robinson-Schensted. Les
propriétés algébriques de cette algèbre de Hopf sont étudiées..
] 01/03/2011
Pierre-Loï Méliot Partitions aléatoires choisies suivant les poids des traces de Markov des algèbres d'Hecke [Slides.pdf ]abstract.htmlÉtant donnée une trace définie sur l'algèbre d'Hecke du groupe
symétrique Sn,
la décomposition de t sur la base des caractères irréductibles fournit
une
mesure de probabilité sur l'ensemble Pn des partitions de taille n.
Lorsque t
est la trace régulière de Hq(Sn), ou plus généralement une trace de
Markov, la
mesure correspondante vérifie une loi des grands nombres et un
théorème
central limite pour la taille des lignes et des colonnes des
partitions. Via
l'algorithme RSK et la théorie des fonctions quasisymétriques, ces
résultats
peuvent être interprétés en termes de longueur des plus longs
sous-mots
croissants et décroissants de modèles de permutations aléatoires.
] 28/02/2011
Pierre Martinetti Séminaire LCR - Von Neumann algebras in physics by examplesabstract.htmlWe will illustrate the importance of von Neumann algebras in physics, emphasizing in particular their role in the algebraic formulation of quantum field theory.
] 22/02/2011
Gérard Duchamp De Lyndon à Lothaire 22/02/2011
Philippe Marchal Marches aléatoires : records, lemme cyclique et convergence presque sûre [Slides.pdf ]abstract.htmlMarches aléatoires : records, lemme cyclique et convergence presque sûre. (Philippe Marchal, LAGA, Paris 13)
] 22/02/2011
Hoang Ngoc Minh Algebraic combinatorial aspects of nonlinear differential systems [Slides.pdf ] 15/02/2011
Cyril Banderier Séance d'exercices autour des mots de Lyndon et de l'inversion de Moebius 15/02/2011
Alexandre Benoit Expansions de Fourier et de Chebyshev de fonctions D-finies [Slides.pdf ]abstract.htmlChebyshev polynomials, Hermite polynomials, Bessel functions and other families of special functions each form a basis of some Hilbert space. A Generalized Fourier Series
is a series expansion in one of these bases, for instance a Chebyshev series. When such a series solves a linear differential equation, its coefficients satisfy a linear recurrence equation.
We interpret this equation as the numerator of a fraction of linear recurrence operators. This interpretation lets us give a general algorithm for computing this recurrence, and a simple view of existing algorithms for several specific function families. Joint work with Bruno Salvy.
] 15/02/2011
Gérard Duchamp Combinatoire de certaines bases dualesabstract.htmlOn donne les notions de factorisation complète du monoïde libre
et fait le lien avec les bases de Radford et leurs duales.
] 08/02/2011
Pierre Martinetti The thermal time hypothesis: geometrical action of the modular group in conformal field theory with boundary [Slides.pdf ]abstract.htmlThe thermal time hypothesis: geometrical action of the modular
group in conformal field theory with boundary.
] 08/02/2011
Pierre Martinetti An algebraic Birkhoff decomposition for non perturbative renormalization [Slides.pdf ]abstract.htmlAn algebraic Birkhoff decomposition for non perturbative
renormalization.
] 08/02/2011
Pierre Martinetti Distances in noncommutative geometry [Slides.pdf ]abstract.htmlDistances in Noncommutative Geometry.
] 01/02/2011
Gérard Duchamp Combinatoire des dérivations extérieures (2/2) 01/02/2011
Benoît Rittaud Mots circulaires, nombres F-adiques et la suite 1, 5, 16, 45, 121, 320, ...abstract.html Un mot circulaire est un mot fini dans lequel on suppose que la
première lettre suit la dernière. On le dit admissible s'il ne
contient que des 0 et des 1 sans jamais voir deux 1 de suite. Les
mots circulaires admissibles renferment des structures explicites de
groupes abéliens finis liés à la suite 1, 5, 16, 45, 121, 320,...
par ailleurs connue pour ses propriétés combinatoires. Une
application des mots circulaires admissibles est l'étude des nombres
"F-adiques", qui sont un équivalent des p-adiques pour le système de
numération déduit de la propriété de Fibonacci (https://oeis.org/A004146).
] 01/02/2011
Gérard Duchamp Combinatoire des dérivations extérieures (1/2) 26/01/2011
Journées Combinatoire de Bordeaux (du mercredi 26 janvier au vendredi 28)25/01/2011
Collectif
Table ronde sur les méthodes orbitales en combinatoire 18/01/2011
Gérard Duchamp Algèbres de substitutions (2/2) 18/01/2011
Matthieu Deneufchâtel About different kinds of substitutions [Slides.pdf ] 18/01/2011
Gérard Duchamp Algèbres de substitutions (1/2) 11/01/2011
Hoang Ngoc Minh Calculs dans les groupes de Galois différentiels (3/3) 11/01/2011
Guoniu Han Formules des équerres pour diverses familles d'arbres et de partitions [Slides.pdf ]abstract.htmlLa formule des équerres (”hook formula”) apparaît dans le contexte des
tableaux de Young
et joue un rôle essentiel en combinatoire algébrique, théorie des
représentations et théorie des partitions.
Une nouvelle méthode, appelée technique de développement en longueur
des équerres (et qui présente quelques challenges algorithmiques),
permet de découvrir toute une famille de formules des équerres, pour
plein de structures combinatoires,
suggérant qu'un phénomène mathématique profond ne nous est
pas encore pleinement révélé.
Un cas particulier de ces formules a été obtenu par Nekrasov et
Okounkov dans un contexte tout à fait différent.
Dans le cas des arbres planaires on obtient une formule qui unifie
plusieurs résultats classiques, y compris la formule de Postnikov.
D’autres travaux récents liés à ce sujet par Stanley, Ono, Bessenrodt,
Carde, Loubert, Potechin, Sanborn, Okada et Panova seront présentés,
ainsi que des liens avec de célèbres conjectures de Ramanujan-Lehmer
sur certaines formes modulaires en théorie des nombres...
] 11/01/2011
Christian Lavault q -analogues04/01/2011
Hoang Ngoc Minh Calculs dans les groupes de Galois différentiels (2/3) 04/01/2011
Matthieu Josuat-Vergès Une "version finie" du produit triple de Jacobi, via chemins et fractions continues [Slides.pdf ]abstract.htmlLe produit triple de Jacobi est une identité reliant un produit infini à une somme infini,
un cas particulier célèbre étant le théorème pentagonal d'Euler. Nous montrons ici
une version finie consistant à dire que les sommes tronquées comptent
certains chemins (ou que leur série génératrice s'écrit comme une fraction continue).
Ceci est relié à des problèmes d'énumération, via certaines formules dites de Touchard-Riordan.
] 04/01/2011
Gérard Duchamp Calculs dans les groupes de Galois différentiels (1/3) 14/12/2010
Ladji Kané Faà di bruno, orbite finie et fonctions rationnelles sur un groupe 14/12/2010
Hoang Ngoc Minh Dérivées successive de la série des Polylogs et Formule de Faà di Bruno 14/12/2010
Laurent Poinsot Faà di Bruno, orbite finie et fonctions rationnelles sur un groupe [Slides.pdf ] 07/12/2010
Gérard Duchamp Équations différentielles non commutatives 07/12/2010
Mario Valencia-Pabon Partitions de produits de graphes complets en ensembles dominants indépendants [Slides.pdf ] [abstract.pdf ] 07/12/2010
Gérard Duchamp Triangularité et théorème(s) de Radford 30/11/2010
Laurent Poinsot Séance interactive sur les polyzêtas (2/2) 30/11/2010
Jean-Éric Pin Une extension aux mots du théorème de Mahler [Slides.pdf ] 30/11/2010
Hoang Ngoc Minh Séance interactive sur les polyzêtas (1/2) 23/11/2010
Adrian Tanasa Discussion à la suite de "Renormalizability in (non)commutative quantum field theory" [Slides.pdf ]abstract.htmlI will introduce in this talk the main ingredients required to obtain a renormalizable model in quantum field theory.
] 23/11/2010
Adrian Tanasa Renormalizability in (non)commutative quantum field theoryabstract.htmlI will introduce in this talk the main ingredients required to obtain a renormalizable model in quantum field theory.
] 23/11/2010
Hoang Ngoc Minh Sur la renormalisation de polyzêtas divergents 16/11/2010
Christophe Tollu Processus déterminantaux (2/2) 16/11/2010
Nikolaos Fountoulakis 3-connected cores in random 2-connected graphs [Slides.pdf ] 16/11/2010
Christophe Tollu Processus déterminantaux (1/2) 09/11/2010
Ladji Kane Indexation de Lyndon des polynômes irréductibles sur un corps à q éléments 09/11/2010
Rafik Aguech Fragmentations aléatoires [Slides.pdf ] 09/11/2010
Gérard Duchamp K < x > en tant qu'algèbre enveloppante, caractéristique nulle et positive02/11/2010
Laurent Poinsot Adjonction d'unité, aspect catégorique [Slides.pdf ]abstract.htmlAdjonction d'unité, aspect catégorique.
] 02/11/2010
Olivier Bodini Génération aléatoire via la méthode de Boltzmann 02/11/2010
Gérard Duchamp Autour de la relation d'Heisenberg AB-BA=I 26/10/2010
Gérard Duchamp Dual de Sweedler et forme sandwich 26/10/2010
Roland Bacher Exponentielles de séries génératrices exponentielles [article.pdf] 26/10/2010
Matthieu Deneufchâtel Exemples et calculs sur les duals de Sweedler [Slides.pdf ] 19/10/2010
François Bergeron Discussion 19/10/2010
François Bergeron Combinatoire de Catalan et des fonctions de stationnement [Slides.pdf ]abstract.htmlAu cours des dernières années, des questions soulevées en théorie des invariants de groupes, concernant les propriétés des espaces coinvariants diagonaux, ont mené à une étude fine de la combinatoire des fonctions de stationnement (parking functions) et de paramètres sur celles-ci. Nous allons présenter certains de ces développements, ainsi que des extensions qui font intervenir l'ordre de Tamari et ses extensions aux cas des chemins de Dyck généralisés.
] 19/10/2010
François Bergeron SLk pavages de Z xZ [Slides.pdf ] 05/10/2010
Brigitte Vallée Discussion 05/10/2010
Brigitte Vallée Analyse des algorithmes euclidiens et opérateurs de Ruelle [Slides.pdf ] 05/10/2010
Brigitte Vallée Systèmes dynamiques, opérateurs de transfert et analyse fonctionnelle [Slides.pdf ] 28/09/2010
Julien David (soutenance de thèse à Marne-la-Vallée) 28/09/2010
Gérard Duchamp Polynômes orthogonaux comprimés et états cohérents 21/09/2010
Andrea Sportiello Limit shapes in random tiling models: a geometric approach [Slides.pdf ] 21/09/2010
Laurent Poinsot Sur le plongement du complété d'un espace normé dans son complété pour une autre norme [Slides.pdf ]abstract.html
] 21/09/2010
Gérard Duchamp Un opérateur transcendant dans le noyau de la transformation Gelfand décrit par un modèle particulaire 06/09/2010
Mark Wilson Higher order asymptotics from multivariate generating functions [Slides.pdf ] 20/07/2010
Hoang Ngoc Minh Analytic and combinatoric aspects of Hurwitz polyzêtas [article.pdf avec Jean-Yves Enjalbert] 20/07/2010
Pawel Hitczenko Restricted Compositions with same number of parts 20/07/2010
Clôture de l'année académique par un repas "CALIN" de fin d'année 20/07/2010
Hanane Tafat , Cyril Banderier Grammaires algébriques et asymptotique [Slides.pdf ]abstract.htmlGrammaires algébriques et asymptotique.
] 08/07/2010
Journée de présentation des sujets de recherche des nouveaux stagiaires et doctorants de l'équipe CALIN : Gora Adj, Sven De Félice, Sandrine Dasse-Hartaut, Omar Ait Mous, Matthieu Deneufchâtel, Hanane Tafat Bouzid. 06/07/2010
Gérard Duchamp Espaces rationnels de fonctions sur un groupe : application à l'algèbre de Hopf de Faà di Bruno 29/06/2010
Christophe Tollu Fonctions harmoniques et bord de Martin, le cas discret ( 2/2) 29/06/2010
Christophe Tollu Fonctions harmoniques et bord de Martin, le cas discret (1/2) 22/06/2010
Gérard Duchamp Bidual de Sweedler et rationalité 22/06/2010
Silvia Goodenough Formule de Faà di Bruno et continuité partielle 15/06/2010
Hoang Ngoc Minh TBA 15/06/2010
Andrea Sportiello Approximations de π et modèle à six sommets 01/06/2010
Laurent Poinsot Dualité et séries formellesabstract.htmlDualité et séries formelles.
] 01/06/2010
Gérard Duchamp Dualité algébrique et continue en Informatique 25/05/2010
Silvia Goodenough Déformations d'algèbres de Hopf 25/05/2010
Alfredo Viola Linear Probing Hashing 18/05/2010
Hayat Cheballah Construction partielle de la bijection Gog-Magog 18/05/2010
Jean Cardinal Sorting under partial information (without the ellipsoid algorithm) 18/05/2010
Hoang Ngoc Minh Une preuve par indiscernabilité 11/05/2010
Xavier Viennot (LaBRI) Combinatoire bijective et "interactions"... 11/05/2010
Alain Lascoux (IGM) Quelques bijoux de combinatoire algébrique 11/05/2010
Andrea Sportiello (Université de Milan, Italie) Preuve de la conjecture de Razumov-Stroganov 11/05/2010
Philippe di Francesco (CEA) Physique et combinatoire 11/05/2010
Christian Krattenthaler (Université de Vienne, Autriche) Calcul avancé de déterminants et calcul de π 11/05/2010
Conrado Martinez (Université Polytechnique de Catalogne, Espagne) Searching with dices : A survey on randomized data structures 11/05/2010
Philippe Flajolet (INRIA / Académie des Sciences) Analyse d'algorithmes et combinatoire analytique 11/05/2010
"Journée CALIN" Inauguration de la nouvelle équipe de combinatoire 04/05/2010
Matthieu Deneufchâtel Le shuffle et ses q -déformations 04/05/2010
Gérard Duchamp q -déformations du shuffle et Physique27/04/2010
Andrzej Horzela The φ4 model in QFT : nonlinearity, Feynman graphs and renormalization 13/04/2010
Gérard Duchamp Exercices sur les fonctions D-finies 13/04/2010
Xavier Provençal Combinatoire des mots et convexité discrète 13/04/2010
Cyril Banderier Exercices sur les fonctions D-finies 06/04/2010
Kirone Mallick Solutions exactes pour le processus d'exclusion asymétrique [Slides.pdf ] 06/04/2010
Damien Régnault Automates cellulaires stochastiques et modélisation de la formation des quasi-cristaux 06/04/2010
Kirone Mallick Discussion sur les structures algébriques des q-analogues et de la supersymétrie 30/03/2010
Dominique Manchon Renormalisation des valeurs zêta multiples aux entiers négatifsabstract.htmlRenormalization of multiple zeta values for negative integers.
Using Connes and Kreimer renormalization, we will show how
to extend multpiple zeta functions to every complex argument
so that the "quasi-abattage" relations are preserved.
The values obtained for negative integers are rational.
We will discuss a multi-dimensional analogue.
Common work with Sylvie Paycha.
] 30/03/2010
Jean Fromentin Algorithmique des tresses : la forme normale tournanteabstract.htmlUne tresse, est un objet géométrique composé de brins qui se croisent.. En mettant bout à bout deux tresses ayant le même nombre de brins, on obtient une nouvelle tresse. Munis de cette opération, l’ensemble des tresses à n brins forme un groupe. Une présentation, par générateurs et relations de ce groupe, est donnée en 1942 par Artin. Une tresse peut alors être vue comme une classe d’équivalence de mots de tresse. Une forme normale est alors un moyen (souvent algorithmique) de sélection pour une tresse d’une mot de tresse distingué la représentant.
L’exposé sera divisé en deux parties. La première sera consacrée à une introduction aux groupes de tresses : point de vue intuitif, structure de groupe, présentation d’Artin, problème du mot, etc. Dans la seconde, je présenterai l’objet central de mes travaux, qui est une nouvelle forme normale des tresses, dite forme normale tournante, et j’expliquerai (un peu) en quoi cette nouvelle forme est intéressante, notamment en liaison avec l’ordre de Dehornoy des tresses. Ensuite, je me concentrerai sur les aspects plus informatiques de cette approche, à savoir la construction d’automates explicites reconnaissant les formes tournantes. Seuls les idées seront présentées dans cet exposé, les détails techniques seront volontairement omis.
] 30/03/2010
Dominique Manchon TBA 23/03/2010
Adrian Tanasa Algèbres de Hopf combinatoires dans les théories quantiques des champs 23/03/2010
Andrea Sportiello A combinatorial proof of the Razumov-Stroganov conjecture 23/03/2010
Gérard Duchamp Physique Combinatoire : Peut-on se passer de l'analyse fonctionnelle ? 23/03/2010
Andrzej Horzela TBA 16/03/2010
Pawel Blasiak Graph Model of the Heisenberg-Weyl algebraabstract.htmlThe Heisenberg-Weyl algebra, underlying most physical realizations of Quantum Theory,
is considered from a combinatorial point of view. We construct a concrete model
of the algebra in terms of graphs which endowed with intuitive concepts of composition
and decomposition provide a rich bi-algebra structure.
] 16/03/2010
Pawel Blasiak TBA 09/03/2010
Angela Mestre On the Feynman graph expansion of 1-particle irreducible n-point functions in quantum field theory [Slides.pdf ] 09/03/2010
Gérard Duchamp Sur les structures algébriques de la physique (discussion) 02/03/2010
Cyril Banderier Survey sur "combinatoire et holonomie" 16/02/2010
Ali Akhavi Analyse symbolique des algorithmes de recherche de séquence génératrice optimale dans une structure présentéeabstract.htmlPour étudier un algorithme de tri classique sur $n$ nombres réels distincts, il suffit d'étudier l'algorithme sur les antécédents de $(1,2,...,n)$, i.e. sur les $n!$ énumérations des éléments de l'ensemble $\{1,...,n\}$. L’exécution de l’algorithme sur l'ensemble de ces $n!$ énumérations permet de constater toutes les exécutions possibles de l'algorithme.
Lorsque les algorithmes sont décrits à la manière des systèmes dynamiques symboliques, chaque exécution est une suite de transformations élémentaires. Afin de caractériser parmi tous les mots sur l'alphabet des transformations élémentaires, ceux qui correspondent à des traces d'exécutions, il suffit donc pour les tris classiques de considérer les traces d'exécutions sur un ensemble générique : l'ensemble des énumérations des éléments de l'ensemble $\{1,...,n\}$.
Nous fournissons un cadre permettant d'exhiber de tels ensembles génériques d’entrées pour les algorithmes de recherche de séquence génératrice optimale dans une structure présentée (les tris en sont des exemples particuliers mais cela englobe aussi les algorithmes d’Euclide de Gauss et bien d'autres).
Une structure présentée est une structure munie d'un squelette pour sa présentation (ou encore son codage) : un entier pour le cardinal d'une séquence génératrice et un ensemble de mots correspondants aux relateurs. Nous nous intéressons à de tels objets munis d'un préordre, lorsqu'ils possèdent beaucoup (éventuellement une infinité) de séquences génératrices. Nous considérons les algorithmes qui partant d’une séquence génératrice quelconque retournent une séquence génératrice satisfaisant certaines propriétés vis-à-vis du préordre.
] 16/02/2010
Christian Lavault q -series et leurs applications combinatoires et physiques16/02/2010
Aloïs Panholzer Some applications of the method of moments in the analysis of algorithms [Slides.pdf ] 09/02/2010
Aloïs Panholzer Exact and asymptotic enumeration results for combinatorial objects [Slides.pdf ] 09/02/2010
Christian Lavault q -analogues et notations de Dirac09/02/2010
Gérard Duchamp Exponentielles, équations d'évolution et fonctions symétriques (commutatives et non-commutatives) 02/02/2010
Matthieu Deneufchâtel Asymptotique de certaines intégrales de Selberg: le cas unitaire et la transformée binomiale 02/02/2010
Gérard Duchamp Fin de l'atelier du 05 janvier 26/01/2010
François Delbot Comparaison et évaluation en moyenne de processus d'optimisation pour le problème du vertex coverabstract.htmlLa théorie de la complexité distingue les problèmes que l’on sait résoudre en un temps polynomial en la taille des données (que l’on peut qualifier de raisonnable), des problèmes NP-complets, qui nécessitent (en l’état actuel des connaissances) un temps de résolution exponentiel en la taille des données (que l’on peut qualifier de déraisonnable).
C’est pour cette raison que la communauté scientifique s’est tournée vers les algorithmes (polynomiaux) d’approximation dont la mesure de qualité se fait le plus souvent grâce au rapport d’approximation en pire cas (pour un problème de minimisation de taille, un algorithme a un rapport d’approximation de k si la taille de toute solution pouvant être retournée par l’algorithme est inférieure ou égale à k fois la taille de la solution optimale).
Dans la littérature, on en vient à considérer qu’un algorithme est plus performant qu’un autre lorsqu’il possède un plus petit rapport d’approximation en pire cas. Cependant, il faut être conscient que cette mesure, désormais "classique", ne prend pas en compte la réalité de toutes les exécutions possibles d’un algorithme (elle ne considère que les exécutions menant à la plus mauvaise solution).
Dans les travaux que je vais vous présenter, nous avons tenté de mieux "capturer" le comportement des algorithmes d’approximation en allant plus loin que le simple rapport d’approximation en pire cas (en nous focalisant sur le problème du Vertex Cover) :
En montrant que les performances moyennes d’un algorithme peuvent être décorélées des performances en pire cas. Par exemple, nous avons montré que dans la classe des graphes spécialement conçus pour le piéger en pire cas, l’algorithme glouton "Maximum Degree Greedy" retourne, en moyenne, des solutions dont la taille tend vers l’optimum lorsque n tend vers l’infini.
En évaluant les performances moyennes d’un algorithme. Nous avons prouvé que l’algorithme online présenté par Demange et Paschos en 2005 (dont le rapport d’approximation en pire cas est égal au degré maximum du graphe) est au plus 2-approché en moyenne dans n’importe quel graphe. Ce résultat, combiné à d’autres, montre que cet algorithme est "en pratique" meilleur que la plupart des algorithmes 2-approchés connus, malgré un mauvais rapport d’approximation en pire cas .
En comparant les performances de différents algorithmes (analytiquement et expérimentalement). Nous avons proposé un algorithme de liste et nous avons prouvé analytiquement qu’il retourne toujours une meilleure solution que celle construite par un autre algorithme de liste récent [ORL 2006] quand ils traitent la même liste de sommets (dans certains graphes particuliers, la différence de taille peut être arbitrairement grande).
Nous avons également comparé analytiquement (en utilisant des outils comme les séries génératrices) les performances moyennes de six algorithmes sur les chemins. Nous les avons ensuite expérimentées sur un grand nombre de graphes de diverses familles bien choisies.
On constate dans ces études que les algorithmes 2-approchés étudiés sont ceux qui obtiennent les plus mauvaises performances en moyenne et que ceux qui ont les meilleurs comportements moyens ont de mauvais rapports d’approximation (fonction du degré max. du graphe).
Tous ces résultats montrent que le rapport d’approximation en pire cas n’est pas toujours suffisant pour caractériser l’intégralité de la qualité d’un algorithme et que d’autres analyses (en moyenne notamment) doivent être effectuées pour en faire le tour.
] 26/01/2010
Christophe Tollu Réalisation de certaines algèbres d'opérateurs à l'aide de la combinatoire des mots 19/01/2010
Christian Lavault Emergence et applications des q -analogues 19/01/2010
Andrea Sportiello Clifford representation of an algebra related to spanning forests [Slides.pdf ] 12/01/2010
Christian Brouder De l'algèbre de Hopf des polynômes à celle de la renormalisation (2/2) 12/01/2010
Antoine Genitrini Expressions booléennes aléatoires : probabilités, complexité et comparaison quantitative de logique propositionnelle [Slides.pdf ]abstract.htmlÉcrivez une formule booléenne de manière aléatoire, construite avec des ensembles fixés de connecteurs et de littéraux. Quelle est la fonction booléenne « typique » qu’elle représente ? Quelle est la probabilité que la formule calcule la fonction Vrai ? Un littéral ? Ou une autre fonction donnée ? D’autres questions de nature un peu différente peuvent se poser : quelle est la complexité de la fonction booléenne représentée par cette formule aléatoire (i.e. la taille de la plus petite formule la représentant) ? Quelle est la complexité moyenne d’une fonction booléenne définie sur k variables ?
Ces questions mettent en avant le problème suivant : comment définir une distribution de probabilité sur les fonctions booléennes ? Les premiers articles se posant ce genre de questions ont mis en avant deux modèles de formules booléennes aléatoires, basées sur les connecteurs binaires Et/Ou, et qui engendrent une distribution (non uniforme) sur les fonctions booléennes. Ces articles n’ont répondu que très partiellement aux premières questions que j’ai évoquées. On adapte aisément ces distributions au cas de formules construites à l’aide de l’unique connecteur Implication, un des connecteurs de base d’un point de vue logique. Ce modèle de base suscite de l’intérêt car certaines formules représentant des tautologies (formule calculant toujours Vrai) en logique classique ne sont pas des tautologies en logique intuitionniste.
Dans un premier temps, j’exposerai les résultats concernant l’ensemble des fonctions booléennes construites sur l’Implication, puis j’aborderai en détail les tautologies. Dans un troisième temps, j’enrichirai le modèle de formules en utilisant plusieurs connecteurs logiques aléatoires. Enfin, je conclurai l’exposé en abordant différentes perspectives relatives à ces problèmes et sur lesquelles je travaille actuellement.
] 12/01/2010
Christian Brouder De l'algèbre de Hopf des polynômes à celle de la renormalisation (1/2) 05/01/2010
Gérard Duchamp Quelques groupes de Lie de dimension infinie utiles en Combinatoire 05/01/2010
Gérard Duchamp Atelier: Exercice 5.37 de Stanley, Enumerative Combinatorics 22/12/2009
Rafik Aguech 22/12/2009
Kamel Mazhouda Critère de positivité de Li et l'hypothèse de Riemann [Slides.pdf ] 22/12/2009
Cyril Banderier Mellin et sommes harmoniques 15/12/2009
Laurent Poinsot Formule d'inversion de Möbius et monoïde à zéro 15/12/2009
Yann Ponty Repliement de l'ARN : Une approche combinatoireabstract.htmlHistoriquement, l’ADN et les protéines, aux deux extremités du dogme central de la biologie moléculaire, ont monopolisé l’attention des chercheurs en biologie, délaissant dans un premier temps l’ARN, confinée dans un rôle d’intermédiaire. Cependant, des études menées au cours de la dernière décennie sur les mécanismes de fonctionnement de ce polymère ont révélé une diversité de modes d’actions et un potentiel thérapeutique tels que deux prix Nobels ont été décernés à C. Mello/A. Z. Fire (Médecine 2006) et V. Ramakrishnan/T. A. Steitz/A. E. Yonath (Chimie 2009).
À l’échelle nanométrique des interactions moléculaires, il est possible d’analyser la fonction des molécules à travers leur géométrie, ou conformation. Dans le cas de l’ARN, la conformation fonctionnelle d’un ARN résulte de phénomènes d’appariement entre des bases complémentaires, qui provoquent un repliement global de l’ARN. Par ailleurs, des contraintes stériques permettent bien souvent de limiter l’ensemble des conformations possible à des structures simples, les structures secondaires, dans lesquels les appariements considérés sont sans croisement. On assimile alors cet ensemble à un ensemble canonique "de Boltzmann", un des objets de base de la physique statistique, ce qui permet de définir une distribution de probabilité, dite de Boltzmann, sur l’ensemble des structures secondaires réalisables. L’ensemble des conformations d’un ARN est aussi assimilable à un objet combinatoire simple, analogue d’un arbre ou encore d’une séquence bien parenthésée, et pouvant être étudié grâce à l’arsenal de la combinatoire analytique.
Après une introduction présentant les problématiques et challenge actuels de la bioinformatique de l’ARN, nous présenterons deux contributions à l’algorithmique des structures d’ARN, reposant sur une vision combinatoire de l’ensemble des conformations.
La première consiste en une analyse et une amélioration d’un algorithme d’échantillonnage statistique pour la structure d’ARN. En se basant sur une analogie avec la génération aléatoire par la méthode dite récursive, nous pratiquons une analyse de la complexité moyenne de l’algorithme, et proposons une amélioration algorithmique basée sur un parcours "Boustrophedon" proposé par Flajolet/Zimmermann/Van Cutsem 1994.
La deuxième application consiste en l’analyse d’une représentation hierarchique pour l’ensemble de Boltzmann, les RNA Shapes introduites par Giegerich/Voß/Rehmsmeier 2004.. Cette hierarchie de représentations compactes pour la structure d’ARN permet la mise en oeuvre d’approches modulaires pour l’analyse des repliements. Cependant, ces approches exigent parfois une énumération exhaustives des Shapes compatibles avec un ARN, provoquant ainsi une explosion combinatoire qu’il convient de quantifier. Pour cette raison, nous avons modélisé et énuméré celles-ci, obtenant des croissances asymptotiques en $\Theta(A^n/n^{3/2})$ pour ces représentations, avec A=1.8... (resp. A=1.3) pour la représentation la moins (resp. la plus) compacte, à comparer avec A=2.3 pour le nombre de structures secondaires de taille similaire.. Au passage, nous montrons (encore une...) bijection entre le niveau de représentation le plus compact et les mots de Motzkin.
Les travaux sur les RNA-Shapes ont été menés en collaboration avec A. Lorenz et P. Clote (Boston College).
] 08/12/2009
Roland Berger Algèbres de Koszul et combinatoire des mots 08/12/2009
Mathilde Bouvel Motifs et classes de permutations : le point de vue des arbres de décompositionabstract.htmlDans cet exposé, on étudie les classes de permutations, qui sont des ensembles de permutations fermés par le bas pour la relation d’ordre de motif. Je présenterai d’une part des résultats de nature algorithmique sur la recherche de motif dans les permutations, et d’autre part des résultats plutôt combinatoires sur la structure des classes de permutations. Un point commun à ces résultats est qu’ils ont été obtenus en utilisant les arbres de décomposition des permutations. Je présenterai ces objets, et illustrerai par des exemples comment ils peuvent être utilisés en combinatoire comme en algorithmique.
] 08/12/2009
Roland Berger Combinatoire des mots et algèbres de Koszul 01/12/2009
Gérard Duchamp Shuffle, stuffle et commultiplications 24/11/2009
Christophe Tollu Matrices de Wigner : Traces, moments, convergence faible et combinatoire (2/2) 24/11/2009
Christophe Tollu Matrices de Wigner : Traces, moments, convergence faible et combinatoire (1/2) 17/11/2009
Christophe Tollu Transformée de Gelfand et transformée de Fourier 17/11/2009
Matthieu Deneufchâtel Algorithme de calcul rapide d'intégrales de type Selberg 10/11/2009
Laurent Poinsot Monoïde partiel libre (2/2) 10/11/2009
Vonjy Rasendrahasina MAX-2-XORSATabstract.htmlNous présentons une approche analytique du problème d’optimisation MAX-2-XORSAT basée sur la combinatoire analytique et énumérative. Dans cet exposé, nous étudions les séries génératrices liées aux configurations optimales de MAX-2-XORSAT. En combinant ces outils avec ceux d’analyse complexe, nous quantifions alors le nombre maximum de clauses satisfaisables des instances aléatoires de MAX-2-XORSAT.
] 03/11/2009
Gérard Duchamp Théorème de Carter et déformation de Hoffman 03/11/2009
Julien David Analyse de la complexité moyenne de l'algorithme de Mooreabstract.htmlDans un premier temps, on présentera une méthode de génération aléatoire d’automates déterministes accessibles complets et un outil, REGAL, utilisant cette méthode. Les générateurs implantés dans REGAL permettent d’engendrer des automates de plusieurs milliers d’états et ce faisant, d’établir des conjectures crédibles sur les propriétés en moyenne des automates, ainsi que sur les algorithmes qui s’y appliquent.
Dans une deuxième partie, on présentera un résultat théorique sur la complexité moyenne de l’algorithme de Moore: si la complexité dans le pire cas de l’algorithme est connu pour être en $\mathcal{O}(n^2)$, on montrera que pour un alphabet fini arbitraire et la distribution uniforme sur l’ensemble des automates déterministes accessibles complets n états, la complexité moyenne est $\mathcal{O}(n\log n)$.
] 03/11/2009
Silvia Goodenough Algèbres d'incidence (d'après W.Schmitt) 27/10/2009
Hayat Cheballah Mesure de Plancherel sur le graphe de Young Fibonacci 27/10/2009
Gérard Duchamp Traces, caractères et transformation de Gelfand (Exemples) 20/10/2009
Christophe Tollu Partitions aléatoires et processus ponctuels (d'après divers auteurs) (2/2) 20/10/2009
Christophe Tollu Partitions aléatoires et processus ponctuels (d'après divers auteurs) (1/2) 13/10/2009
Laurent Poinsot Monoïde partiel libre (1/2) 13/10/2009
Gérard Duchamp Combinatoire de la formule de Kilmoyer 06/10/2009
Gérard Duchamp Combinatoire des extensions centrales de Heisenberg-Weyl 06/10/2009
Gérard Duchamp Combinatoire des opérateurs diagonaux et applications 29/09/2009
Laurent Poinsot Monoïdes partiels et monoïdes à zéro 29/09/2009
Guilhem Semerjian Physique statistique et SAT aléatoire [Slides.pdf ]abstract.htmlDans les années 90 des simulations numériques ont révélées des propriétés intéressantes dans les ensembles aléatoires d’instances de problèmes de satisfaction de contraintes (satisfiabilité, coloriage de graphes notamment). Quand un paramètre définissant l’ensemble aléatoire (le nombre de clauses par variables) augmente la probabilité de trouver une formule satisfiable chute abruptement de 1 à 0 dans la limite des grandes tailles de formule. Ce phénomène de seuil a été l’objet d’actives recherches en informatique et en probabilités. Par ailleurs des outils (non-rigoureux) de physique statistique ont pu être appliqués à ces problèmes. Un certain nombre de résultats ont émergé de ces études, par exemple des conjectures quantitatives sur la valeur du seuil de satisfiabilité, et une image plus précise de la structure de l’ensemble des solutions des formules satisfiables. D’autres résultats de physique statistique ont un aspect plus algorithmique, que ce soit l’analyse d’algorithmes déjà existants ou la suggestion de nouvelles stratégies pour résoudre ces formules aléatoires. Dans ce séminaire j’essaierai de présenter, sans rentrer dans les détails techniques, le cadre général de ces études et certains de ces résultats.
] 29/09/2009
Gérard Duchamp groupe de travail 22/09/2009
Matthieu Deneufchâtel Symmetric Functions and integrable many body systems [Slides.pdf ] 22/09/2009
Hoang Ngoc Minh L'action du groupe de Galois différentiel des polylogarithmes sur leur développement asymptotique (2/2) 22/09/2009
Gérard Duchamp L'opérateur de déplacement en optique quantique (propriétés et combinatoire ) 15/09/2009
Gérard Duchamp États cohérents quantiques et problème des moments 15/09/2009
Hoang Ngoc Minh L'action du groupe de Galois différentiel des polylogarithmes sur leur développement asymptotique (1/2) 08/09/2009
Christophe Tollu z -mesures et correspondance RSK08/09/2009
Hayat Cheballah Introduction à Sage, Sage-Combinat 07/07/2009
Christophe Tollu Sur l'origine des z -mesures (d'après Kerov, Olshanski, Vershik) 07/07/2009
Hayat Cheballah Processus limite sur le bord du treillis de Young (d'après Borodin et Olshanski) 30/06/2009
groupe de travail 30/06/2009
groupe de travail 23/06/2009
Mario Valencia-Pabon Homomorphismes dans les graphes : applications et problèmes 23/06/2009
Laurent Rigal Sur quelques aspects combinatoires des algèbres quantiques 16/06/2009
Sidi-Mohamed Sedjelmaci Méthode du cercle et coprimalité 16/06/2009
Olivier Gérard Suites coalescentes, mots radio-actifs et autres généralisations de la factorielle 02/06/2009
Christophe Tollu Processus stochastiques sur les graphes de branchements 02/06/2009
Gérard Duchamp Structures partiellement commutatives (3/3) : fonction de Mobius, factorisations critiques et formules de Witt 26/05/2009
Christophe Tollu TBA 26/05/2009
Gérard Duchamp Structures partiellement commutatives (2/3) : réécritures, fonction de Moebius, formules de Witt et classes circulaires 19/05/2009
Gérard Duchamp Structures partiellement commutatives (1/3) : élimination de Lazard 12/05/2009
Silvia Goodenough Opérateurs de symétrisation 12/05/2009
Gérard Duchamp Un programme de Physique Combinatoire 05/05/2009
Gérard Duchamp Algèbre de Hopf de réarrangements (d'après W. Schmitt) 05/05/2009
Christophe Tollu TBA 28/04/2009
Laurent Poinsot Monoides partiels et algèbres booléennes 21/04/2009
Christophe Tollu Produits infinis et combinatoire analytique 07/04/2009
Gérard Duchamp Noncommutative q -on algebra 07/04/2009
Gérard Duchamp Identities in the braid algebra and a conjecture of Don Zagier 31/03/2009
Christophe Tollu z -mesures sur les partitions et théorie des représentations (d'après Kerov, Okounkov, Olshanski et d'autres)31/03/2009
Andrzej Horzela Quantization and combinatorics (3/3): other quantization schemes 24/03/2009
Gérard Duchamp NCSF, théorie des langages et superalgèbres 24/03/2009
Andrzej Horzela Quantization and combinatorics (2/3): operator quantization 17/03/2009
Hayat Cheballah Construction algébrique du bord du treillis de Young 17/03/2009
Andrzej Horzela Quantization and combinatorics (1/3): formalisms of classical mechanics 10/03/2009
Gérard Duchamp Superalgèbres de Lie 10/03/2009
Adrien Boussicault La décomposition en éléments simples et les posets 03/03/2009
Alin Bostan The full counting function of Gessel walks is algebraicabstract.htmlThe aim of the talk is to show how a difficult combinatorial problem has been recently solved using an experimental-mathematics approach combined with (rather involved) computer algebra techniques. More precisely, let $f(n,i,j)$ denote the number of lattice walks in the quarter plane which start at the origin, end at the point $(i,j)$, and consist of $n$ unit steps going either west, south-west, east, or north-east. In the early nineties, Ira Gessel conjectured that the sequence of excursions $f(n,0,0)$ is holonomic. We will present the computer-driven discovery and proof of the following generalization, obtained in August 2008 together with Manuel Kauers: the full generating series $F(t,x,y) = \displaystyle{\sum_{i,j,n \geq 0} f(n,i,j) x^i y^j t^n}$ is an algebraic function.
] 03/03/2009
Carine Pivoteau Génération aléatoire de structures combinatoires: la méthode de Boltzmann effective 03/03/2009
Gérard Duchamp Lemme de Levi et diagrammes étiquetés 17/02/2009
Laurent Poinsot Puissances des opérateurs de substitution avec préfonction 17/02/2009
Hayat Cheballah TBA 17/02/2009
Christophe Tollu Déformations de mesures de Plancherel d'après Matsumoto 10/02/2009
groupe de travail 03/02/2009
Hoang Ngoc Minh A propos de certaines constantes de l'analyse combinatoire 20/01/2009
Silvia Goodenough Convolution dans l'algèbre libre et coefficients de la formule CBH 20/01/2009
Christophe Tollu Analyse harmonique sur un treillis : exemple(s) 13/01/2009
Laurent Poinsot Développement d'endomorphismes sur les suites en série infinie 13/01/2009
Gérard Duchamp Convolution 06/01/2009
06/01/2009
Hoang Ngoc Minh Aspects combinatoires algébriques de l'analyse asymptotique des systèmes dynamiques non linéaires avec entrées singulières 16/12/2008
Silvia Goodenough Un travail sur les coefficients des formules de BCH et Dynkin 16/12/2008
Zaid Odibat Fractional Calculus: Definitions, Numerical Methods and Applications in Control Systems and Multi-scale Processes 09/12/2008
Hayat Cheballah Espaces de chemins et fonctions sur les graphes de branchements 09/12/2008
Flavia Bonomo On variations of the graph coloring problemabstract.htmlA coloring of a graph is an assignment of natural numbers to its vertices in such a way that adjacent vertices receive different colors. This well-known problem is a basic model for frequency assignment and resource allocation problems. In order to take into account particular constraints arising in practical settings, more elaborate models of vertex coloring have been defined in the literature. One of such generalized models is the list-coloring problem, which considers a prespecified set of available colors for each vertex. The list-coloring problem is NP-complete even for split graphs, interval graphs, and bipartite graphs.
We consider some particular cases of the list-coloring problem: μ-coloring, where each vertex has its own upper bound for the color to be assigned, and (γ,μ)-coloring, where each vertex has its own lower and upper bounds for the color to be assigned. The μ-coloring problem arises in the context of classroom allocation to courses, where each course must be assigned a classroom which is large enough so it fits the students taking the course. We will present some polynomial time algorithms to solve these problems on classes where list-coloring is NP-complete.
] 02/12/2008
Gérard Duchamp Calculs explicites et deux problèmes ouverts dans DIAG et LDIAG 25/11/2008
Hayat Cheballah TBA 18/11/2008
Frédéric Meunier Atelier de peinture et découpage de collierabstract.htmlLe problème de l’atelier de peinture est un problème simple à formuler et à comprendre, mais extrêmement riche. Par certains aspects, il relève de l’optimisation combinatoire, par d’autres, de la topologie algébrique, par d’autres encore, il est un point d’entrée dans les classes de complexité exotique comme PPA ou PPAD.
] 18/11/2008
Laurent Poinsot Équations différentielles dans les algèbres de Fréchet 04/11/2008
Silvia Goodenough Dérivations et formule CBH 21/10/2008
Laurent Poinsot Séries entières et algèbres de Fréchet 14/10/2008
Christophe Tollu Problèmes de bord et d'asymptotique dans le treillis des compositions 07/10/2008
Hayat Cheballah Treillis des compositions 30/09/2008
Christophe Tollu Problèmes de bord et d'asymptotique pour le treillis des compositions 16/09/2008
Gérard Duchamp Calculs d'orbites monoïdales et linéaires 09/09/2008
Gérard Duchamp Calculs de chemins dans les graphes marqués 24/06/2008
Gérard Duchamp Supersymétrie, cocycles et bicaractères 09/05/2008
Pawel Hitczenko Comment utiliser les martingales 29/04/2008
Gérard Duchamp Évolution des hamiltoniens à plusieurs modes et polyzetas 16/04/2008
Gérard Duchamp Groupes de substitutions : le cas inhomogène 15/04/2008
Matthieu Josuat-Vergès Permutations, orientations acycliques, et motifs évitésabstract.htmlNous allons mettre en correspondance trois sortes d’objets : des permutations (ensemble d’excédences fixés), des orientations acycliques de graphes, et enfin des diagrammes de Young remplis de 0 et de 1 en évitant certains motifs. Les tableaux de permutations font le lien entre la première et la troisième classe d’objets, ici le motif évité est une paire de matrices d’ordre 2. En prenant une autre paire de matrices d’ordres 2, on fait élémentairement le lien entre la deuxième et la troisième classe. Reste à voir que les motifs évités sont équivalents, au sens où ils s’énumèrent de la même façon, ce qui peut se faire par récurrence mais aussi par des bijections. Selon le temps restant, nous montrerons que cette correspondance s’étend à une classe de polyominos bien plus générale que celle des diagrammes de Young.
] 09/04/2008
Pawel Blasiak Graphs for quantum theory: Combinatorial constructions 01/04/2008
Frédérique Bassino Génération aléatoire d'automates déterministes [Slides.pdf ]abstract.htmlCet exposé portera sur la génération aléatoire d’automates finis. Les automates peuvent être vus comme des graphes orientés dont les arêtes sont étiquetées sur un alphabet fini et dont deux sous-ensembles de sommets sont distingués (l’ensemble respectivement des états initiaux et des états finals).
On présentera une bijection entre l’ensemble des automates déterministes et accessibles à n états sur un alphabet fini et des diagrammes particuliers qui peuvent eux-mêmes être représentés comme les partitions d’un ensemble en n sous ensembles non-vides. Ces constructions combinatoires permettent d’estimer asymptotiquement le nombre d’automates à n états.
Cette approche combinatoire a conduit à la conception d’un générateur aléatoire efficace, pour la distribution uniforme sur les automates déterministes à n états : la complexité moyenne en temps du générateur de Boltzmann associé est en O(n3/2). On montrera quelques exemples de résultats expérimentaux obtenus avec la librairie C++ REGAL dans laquelle il est implanté.
[ Travail en collaboration avec Julien David et Cyril Nicaud (IGM). ]
] 25/03/2008
Karol Penson TBA 18/03/2008
Hayat Cheballah Espaces de Fock 11/03/2008
Christophe Tollu Autour de la formule d'Accardi-Bozejko 26/02/2008
Julien Fayolle Analyse de la compression par anti-dictionnaire [Slides.pdf ]abstract.htmlLa compression sans perte d’un texte par anti-dictionnaire (DCA) est une technique de compression efficace introduite par Crochemore et alii à la fin des années quatre-vingt dix. Son principe repose sur la construction de l’anti-dictionnaire du texte : un dictionnaire formé de certains mots n’apparaissant pas dans le texte (mots appelés mots minimaux interdits).
Après une introduction à cet algorithme, je montre que sous un modèle sans mémoire de génération des textes, le nombre moyen de mots dans l’anti-dictionnaire sur l’ensemble des textes de taille n se comporte asymptotiquement en $\frac{Kn}{h}+o(n)$, où la constante $K$ est determinée explicitement et $h$ est l’entropie du modèle probabiliste. Les outils que j’utilise proviennent de la combinatoire analytique et des probabilités.
] 19/02/2008
Pierre Nicodème Counting occurrence of words in random texts [Slides.pdf ]abstract.htmlWe consider random texts generated by a Bernoulli source.
We want to count simultaneously the number of occurrences of words
within a finite set of words in a random text of size
n .
The use of generating functions permits to construct a multivariate
function counting the occurrences in texts of all size from 0 to infinity.
From there several techniques give access to texts of size
n .
We compute the multivariate generating function
by the very elegant analytic inclusion-exclusion method that resorts to combinatorics.
by constructing the Aho-Corasick automaton recognizing the words,
and translating later to generating functions. We compare the complexity of these two methods.
[Joint work with F. Bassino, J. Clément and J. Fayolle].
] 19/02/2008
Hayat Cheballah Groupes algébriques de substitutions approchées et groupe de Riordan 12/02/2008
Jean-Gabriel Luque q -discriminants, hyperdéterminants et polynômes de Macdonald05/02/2008
Pawel Hitczenko Probabilistic take on permutation tableaux [Slides.pdf ]abstract.htmlPermutation tableaux are relatively new combinatorial objects that are in bijections with permutations. They have ben introduced in the context of algebraic combinatorics and subsequently found applications in combinatorial aspects of some particle models (like PASEP). Permutation tableaux have been studied mostly by bijective methods. In this talk, I will describe a direct, elementary approach based on probabilistic interpretation of a basic construction. This talk is partially based on results obtained jointly with Sylvie Corteel.
] 05/02/2008
Laurent Poinsot Fonctions parfaitement non linéaires et partition approchée de l'unité 15/01/2008
Jean Mairesse Tetris, traces, tressesabstract.htmlLe modèle de Tetris sera le fil rouge de l’exposé. Il constitue un paradigme pour différents modèles de Systèmes à Événements Discrets, qui peuvent se voir comme des spécialisations, variations ou extensions de Tetris. Tetris constitue également le point de rencontre de deux classes de modèles mathématiquement intéressantes : les systèmes itérés d’applications topicales (max-plus dans le cas de Tetris) et les marches aléatoires sur les groupes ou monoïdes discrets (traces dans le cas de Tetris). Par ailleurs, le modèle de Tetris est intéressant en lui-même et sera étudié en tant que tel. On s’intéresse aux aspects énumératifs (combien d’empilements différents ?), à l’optimisation (à quoi ressemblent les empilements les plus denses ?) et à l’évaluation de performances (à quelle vitesse se constituent les empilements aléatoires ?).
] 14/01/2008
Allan I. Solomon Introduction to entanglement 08/01/2008
Gérard Duchamp Quelques exercices inédits sur les algèbres de Hopf 11/12/2007
Hsien-Kuei Hwang Uniform asymptotics of Poisson approximation to binomial distribution and its generalizationsabstract.htmlNew uniform asymptotic approximations with error bounds are derived for a generalized total variation distance of Poisson approximation to the Poisson-binomial distribution (covering binomial distribution as special case). The method of proof is also applicable to other Poisson approximation problems, and therefore to a lot of data structures and algorithms.
] 04/12/2007
Cyrille Bertelle , Rawan Ghnemat , Gérard Duchamp Combinatoire et modélisation : ségrégation de Schelling et dérangements généralisés 27/11/2007
Gérard Duchamp Sur le théorème de réciprocité de Frobenius 13/11/2007
Christophe Tollu TBA 06/11/2007
Gérard Duchamp Semigroupes partiels, perturbations de coproduits et applications : infiltration, physique et Hoffmann 30/10/2007
groupe de travail 23/10/2007
Laurent Poinsot Fonctions parfaitement non-linéaires 16/10/2007
groupe de travail 09/10/2007
Christophe Tollu Polytopes et coefficients de Littlewood-Richardson 02/10/2007
Gérard Duchamp Limites projectives et applications en physique 19/06/2007
Christophe Tollu Une approche non commutative du théorème central-limite de Vershik-Kerov (2/2) 12/06/2007
groupe de travail 05/06/2007
Christophe Tollu Une approche non commutative du théorème central-limite de Vershik-Kerov (1/2) 29/05/2007
Frédéric Chyzak Sommation et intégration symboliques des fonctions spéciales et suites combinatoires 29/05/2007
Gérard Duchamp Sommabilité, finitude et rationalité en Informatique et en Physique 29/05/2007
Éric Laugerotte Manipulation d'expressions non commutatives 22/05/2007
groupe de travail 24/04/2007
Gérard Duchamp Notion de sommabilité : applications en informatique et en physique 03/04/2007
Gérard Duchamp États cohérents non conventionnels, résolutions de l'unité et applications 27/03/2007
Gérard Duchamp États cohérents et problème de moments de Stieltjes 13/03/2007
Frédéric Toumazet Le programme SCHUR : fonctions symétriques, groupes et algèbres de Lie, et applications à la physique 06/03/2007
Gérard Duchamp Un groupe de Lie-Fréchet qui intervient en Combinatoire et en Physique 20/02/2007
Christophe Tollu Processus markoviens sur les partitions (d'après Borodin et Olshanski) (2/2) 06/02/2007
Christophe Tollu Processus markoviens sur les partitions (d'après Borodin et Olshanski) (1/2) 16/01/2007
Annick Valibouze Groupes de Galois et idéaux de Galois 19/12/2006
Kurusch Ebrahimi-Fard Relations de Rota-Baxter et bigèbres généralisées 12/12/2006
Christophe Tollu TBA 05/12/2006
groupe de travail 28/11/2006
Gérard Duchamp Espaces de Fock non commutatifs (2/2) : conjecture de Zagier, factorisation dans l'espace des tresses et interpolations de Hopf 21/11/2006
Adrien Boussicault Identités liées aux fonctions de Greene 31/10/2006
Kurusch Ebrahimi-Fard On Connes-Kreimer's Birkhoff decomposition in perturbative Quantum Field Theory 24/10/2006
Christophe Tollu Représentations remarquables du groupe symétrique infini 17/10/2006
Jean-Gabriel Luque Polynômes de période et crochet de Ihara 03/10/2006
Gérard Duchamp Espaces de Fock non commutatifs (1/2): déformations d'algèbres de Hopf 26/09/2006
Muriel Livernet Algèbres de Hopf tordues (2/2) 19/09/2006
Muriel Livernet Algèbres de Hopf tordues (1/2) 28/02/2006
Luaï Jaff Combinatoire des tableaux (oscillants) 21/02/2006
Christophe Tollu Graphe de Young et caractères du groupe symétrique infini 07/02/2006
groupe de travail 31/01/2006
Gérard Duchamp Spécialisations du dual de Sweedler 24/01/2006
Muriel Livernet L'opérade associative et l'ordre de Bruhat faible du groupe symétrique (en collaboration avec M. Aguiar) 17/01/2006
Gérard Duchamp Matrices biinfinies et applications 10/01/2006
Christophe Tollu Combinatoire des algèbres LS (diagrammes de Bratteli) 03/01/2006
groupe de travail 13/12/2005
groupe de travail 06/12/2005
Sébastien Orange TBA 29/11/2005
Bodo Lass Démonstration de la conjecture de Dumont 22/11/2005
groupe de travail 15/11/2005
groupe de travail 08/11/2005
Ephrem Razafimanantsoa Représentations symétriques des polynômes en plusieurs variables 25/10/2005
Gérard Duchamp Algèbre des graphes de Feynman : liens avec FQSym et isomorphismes de Foissy 18/10/2005
groupe de travail 11/10/2005
Gérard Duchamp Algèbre des graphes de Feynman : déformation de coproduits 22/01/2003
Séance de rentrée 31/05/2005
Marcelo Aguiar TBA 24/05/2005
Tyrell McAllister TBA 17/05/2005
Gérard Duchamp Algèbres de Hecke (5/5) : modules indécomposables 26/04/2005
groupe de travail 19/04/2005
groupe de travail 12/04/2005
Gérard Duchamp Algèbres de Hecke (4/5) : calculs explicites dans l'algèbre de Hecke, Hamiltoniens quantiques et théorie de Galois 29/03/2005
Gérard Duchamp Algèbres de Hecke (3/5) : triangle de Cartan-Brauer de Hn (0) 22/03/2005
Christophe Tollu Algèbres de Hecke (2/5) : couples de Gelfand de groupes linéaires p -adiques 15/03/2005
Gérard Duchamp Algèbres de Hecke (1/5) : caractéristique d'Euler-Poincaré et représentations polynomiales des algèbres de Iwahori-Hecke 08/03/2005
Frédéric Toumazet Combinatoire de l'acide chlorhydrique 22/01/2005
groupe de travail 15/02/2005
Bruno Vallette Séries de Hilbert-Poincaré et dualité de Koszul 08/02/2005
Gérard Duchamp Fonctions quasi-symétriques libres 01/02/2005
Frédéric Toumazet Modèle des ruches pour les nombres de Kostka : aspects algorithmiques (avec J. Nzeutchap) 25/01/2005
Éric Laugerotte MuPADabstract.htmlLe langage de programmation de MuPAD est dit catégoriel. On peut le
comparer aux langages de programmation orienté objet mais ici bien
adapté au contexte mathématique et combinatoire. À partir d'un sujet qui
m'occupe en ce moment (les fonctions booléennes et la décomposition
automatique de modules en indécomposables), on détaillera la construction
et la manipulation de domaines en MuPAD.
] 25/01/2005
Christophe Tollu Formes-limites des diagrammes de Young et fonctions sur ces diagrammes 25/01/2005
Gérard Duchamp Algèbre de Hopf des diagrammes et applications 18/01/2005
Jean-Louis Loday Opérades et bigèbres généralisées 11/01/2005
Christophe Tollu Forme-limite des diagrammes de Young et fonctions sur ces diagrammes 22/01/2003
groupe de travail 07/12/2004
Todor Popov 30/11/2004
Christophe Tollu Caractères asymptotiques des groupes symétriques (2e partie) 23/11/2004
Christophe Tollu Caractères asymptotiques des groupes symétriques (1e partie) 16/11/2004
Loï Foissy Algèbre de Hopf de Connes-Kreimer non commutative 09/11/2004
Muriel Livernet Introduction aux opérades 02/11/2004
Jean-Gabriel Luque Calcul de l'intégrale de Selberg par des méthodes hyperdéterminantales 26/10/2004
Gérard Duchamp Algèbres de Hopf de fonctions (2/2) 26/10/2004
Muriel Livernet Théorèmes de Milnor-Moore non commutatifs (d'après Londay-Ronco) 19/10/2004
Vlady Ravelomanana Composante(s) géante(s) dans les graphes et physique statistique 12/10/2004
Muriel Livernet Théorèmes de Milnor-Moore non commutatifs (d'après Loday et Ronco) 28/09/2004
Gérard Duchamp Algèbres de Hopf de fonctions (1/2) 05/05/2004
Michèle Vergne Formules de résidus pour le calcul de fonctions de partitions (dont l'énumération de points entiers dans des polytopes) et de sommes d'Euler-Maclaurin 28/04/2004
groupe de travail 24/03/2004
groupe de travail 05/02/2004
Ronald C. King Atelier 28/01/2004
Charles Cochet Calcul effectif de la fonction de partition vectorielle ; application aux flots dans les réseaux et en théorie des représentations 14/01/2004
Atelier "combinatoire des algèbres de Lie" 17/12/2003
Dualité de Schur-Weyl (groupe symétrique / groupe général linéaire) et extensions d'après Halverson et Ram 22/10/2003
atelier combinatoire des groupes et algèbres de Lie 27/05/2003
Leonid Vainerman Groupes quantiques et fonctions spéciales 27/05/2003
Vlady Ravelomanana Algorithmique distribuée et graphes aléatoires géométriques 27/05/2003
Rémi Monasson Transitions de phase en informatique : de l'approche physique à une analyse rigoureuse 27/05/2003
Karol Penson Extending Dobinski relations: from boson normal ordering to Feynman diagrams 27/05/2003
Cyril Banderier Combinatoire (analytique), informatique (théorique) et physique (statistique) 27/05/2003
Xavier Viennot Empilements de pièces et combinatoire des monoïdes de traces en physique 26/05/2003
Florent Hivert & Nicolas Thiéry Algèbres (de Hopf) combinatoires; implantation (+ démo) 26/05/2003
Grzegorz Pestka Dirac equation and its algebraic approximation 26/05/2003
Abdelmalek Abdesselam Combinatoire du logarithme et renormalisation en physique 26/05/2003
Ronald C. King The square of the Vandermonde determinant and its q -deformation 26/05/2003
Frédéric Toumazet Polynomialité des coefficients de Littlewood-Richardson 26/05/2003
Xavier Viennot La suite magique 1, 2, 7, 42, 429, ... en combinatoire et en physique 26/05/2003
Journées du LIPN (26-27 mai 2003) 14/05/2003
30/04/2003
Emmanuel Briand Polynômes multisymétriques 30/04/2003
Cyril Banderier Combinatoire formelle et calcul analytique 26/03/2003
Daniel Barsky Matrices de Seidel 05/03/2003
Gérard Duchamp Combinatoire des dérivations et des opérateurs caténatifs 26/02/2003
groupe de travail 12/02/2003
Nicolas Thiéry Mupad Combinat : une plate-forme libre de développement collaboratif pour la combinatoire algébrique 05/02/2003
Alain Lascoux Yang-Baxter, glace carrée et variétés de drapeaux 22/01/2003
groupe de travail 08/01/2003
Gérard Duchamp Combinatoire et facteurs de commutation 08/01/2003
Christophe Tollu Réalisabilité des algèbres de Weyl déformées 18/12/2002
Jean-Yves Thibon Un monoïde plaxique pour les arbres binaires 04/12/2002
Karol Penson Dobinski formula revisited 20/11/2002
Gérard Duchamp Combinatoire et facteurs de commutation 20/11/2002
Christophe Tollu Réalisabilité des algèbres de Weyl déformées 06/11/2002
Jean-Gabriel Luque Pfaffiens et Hafniens dans l'algèbre de shuffle 06/11/2002
Frédéric Toumazet Caractères non compacts et physiqueabstract.htmlVenez nombreux ! :-)
]