Conference Proceedings
The CIE2016 Conference proceedings are now avaible online. You can get access to the proceedings via SpringerLink.
Abstract Booklet
You may find the downloadable Abtstract Booklet here.
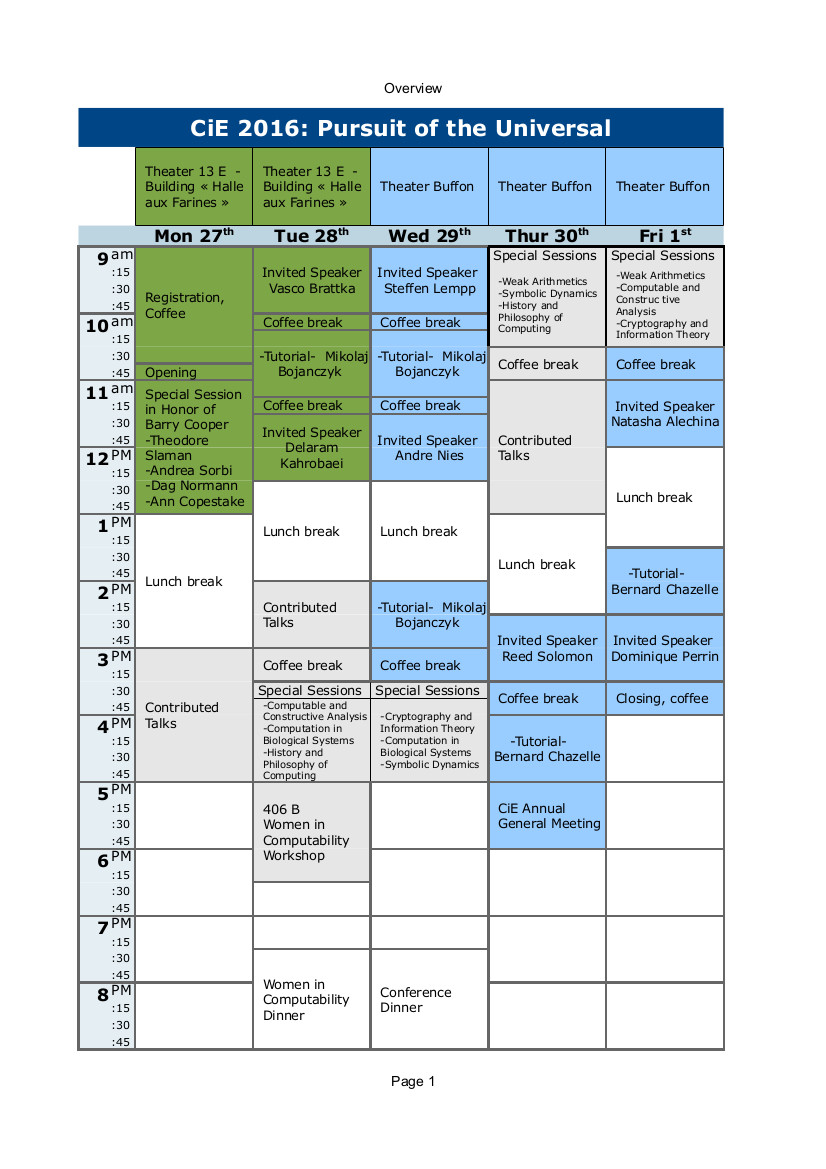
Schedule
The schedule is now avaiable. Click on the image to download it.
Note that plenary sessions on Monday and Tuesday will be held in the Theater 13 E, "Halle aux Farines" Buiding, while plenary sessions on Wednesday, Thursday and Friday will be held in the Buffon Theater.
Special sessions and Contributed talk will take place in the rooms 404B, 405B, 406B and 410B, "Halle aux Farines" Buiding.
Length of Talks
Special Session talks last 45 mins, including questions and turnover (~30 mins talk)
Contributed talks last 30 mins, including questions and turnover (~20 mins talk)
Special Sessions
Special Session in honor of Barry Cooper's memory (organizer: Mariya Soskova)
Speakers
- Theodore Slaman (University of California Berkeley)
- Andrea Sorbi (University of Siena)
- Dag Norman (University of Oslo)
- Ann Copestake (Cambridge University)
Computable and constructive analysis (organizers: Daniel Graça, Elvira Mayordomo)
Speakers
- Mathieu Hoyrup (INRIA and University of Lorraine)
title: The typical constructible object
abstract: Baire Category is an important concept in mathematical analysis. It provides a way of identifying the properties of typical objects and proving the existence of objects with specified properties avoiding explicit constructions. For instance it has been extensively used to better understand and separate classes of real functions such as analytic and smooth functions. Baire Category proves very useful in computability theory and computable analysis, again to understand the properties of typical objects and to prove existence results. However it cannot be used directly when studying classes of computable or computably enumerable objects: those objects are atypical. Here we show how Baire Category can be adapted to such small classes, and how one can define typical computably enumerable sets or lower semicomputable real numbers for instance.
- Arno Pauly (University of Cambridge)
- Vela Velupillai (New School for Social Research in New York City and University of Trento)
- Martin Ziegler (KAIST, Daejeon)
Computation in biological systems (organizers: Alessandra Carbone, Ion Petre)
Speakers
- Daniela Besozzi (University of Milan-Biccocca)
- Eugen Czeizler (Åbo Akademi University)
- Vincent Moulton (University of East Anglia)
title: The wonderful world of RNA
abstract: Boosted by the incredible advances in DNA sequencing, stunning discoveries are being made into how genes and genomes work, and how this knowledge may be applied to important problems in areas such as health, agriculture and human origins. The sister molecule to DNA, RNA, is often less talked about, but current advances concerning this molecule are just as exciting. For example, recent work has shown how RNA’s building blocks may have arisen on early earth, which could have profound consequences on our understanding of the origin of life, and small RNAs have taken center stage in biological systems due their role as key regulators within the cell. RNA molecules are interesting from a computational point of view as they can fold up into tree-like structures which can be efficiently predicted and processed. In this talk, we will review some background concerning the computational biology of RNA, and will discuss some recent results and challenges in this fascinating area of research.
- Eric Tannier (INRIA and University of Lyon)
title: On random graphs and the evolution
abstract: The 1960 paper of Erdös and Renyi was entitled “On the evolution of random graphs”. They mention possible applications in many fields, but not in evolution. I will show such an application. Evolution on genomic sequences will be an accumulation of inversions. I will show that this process is, with a reasonable approximation, similar to the accumulation of edges in a graph, where each vertex i is associated with a probability pi, and an edge is taken with probability pipj. This analogy is helpful to estimate unknown parameters (how many inversions i.e. edges?) from observable ones (how many conserved pairs of consecutive genes i.e. isolated vertices?).
Cryptography and information theory (organizers: Danilo Gligoroski, Carles Padro)
Speakers
- Ludovic Perret (Universite Pierre et Marie Curie, France)
title: Gröbner Bases Techniques in Quantum-Safe Cryptography
abstract: After the publication of Shor’s algorithm it became evident the most popular public-key cryptographic systems that rely on the integer factorization problem or on the discrete logarithm problem would be easily solvable using large enough quantum computers (if such quantum computers are ever built). That triggered a vivid interest in the research of cryptographic algorithms (mostly public-key cryptographic systems) that are resistant to quantum computers. Algebraic cryptanalysis is as a general powerful framework which allow to asses the security of a wide range of cryptographic schemes. The basic principle of such cryptanalysis is to model a cryptographic primitive by a set of algebraic equations. The system of equations is constructed in such a way as to have a correspondence between the solutions of this system, and a secret information of the cryptographic primitive. The key problem in algebraic cryptanalysis is to compute a Gr ̈obner basis of the algebraic equations derived from the cryptographic primitive. It turns that algebraic cryptanalysis can be used to evaluate the security of most quantum-resistant crypto systems proposed so far. The goal of this talk is to quickly discuss of the current intense activity in quantum-resistant cryptography and to present some algebraic attacks against quantum-resistant schemes.
- Ignacio Cascudo (Aalborg University in Denmark)
- Oriol Farras (Universitat Rovira i Virgili, Spain)
- Danilo Gligoroski (Norwegian University of Science and Technology - Trondheim, Norway)
History and philosophy of computing (organizers: Alberto Naibo, Ksenia Tatarchenko)
Speakers
- Maël Pégny (IHPST, Paris)
title: AFCAL as the first computer science association in France - Part I
- Pierre Mounier-Khun (CNRS)
title: AFCAL as the first computer science association in France - Part II
- Simone Martini (Univ. Bologna)
title: Types in programming languages, between modelling, abstraction, and correctness
- Walter Dean (Univ. Warwick)
title: Squeezing feasibility
Symbolic dynamics (organizers: Jarkko Kari, Reem Yassawi)
Speakers
- Valérie Berthé (University Paris 7)
- Emmanuel Jeandel (University of Lorraine)
- Irène Marcovici (University of Lorraine)
- Ronnie Pavlov (Denver University)
title: Computation of topological entropy for Z^2 shifts of finite type
abstract: It has been well-known for some time that the topological entropy of a Z^2 shift of finite type may have no closed form, and in fact may even be noncomputable. For this reason, it’s worthwhile to find provable approximation schemes for the topological entropy of such systems. I will describe some hypotheses which imply approximation schemes for entropy, with varying computation times. The best such results typically leverage uniqueness of the measure of maximal entropy for the system, but I will conclude by outlining recent joint work (with Adams, Briceno, and Marcus) which allows for efficient approximation for some systems where the measure of maximal entropy is not unique.
Weak arithmetics (organizers: Lev Beklemishev, Stanislav Speranski)
Speakers
- Pavel Pudlak (Academy of Sciences of the Czech Republic)
title: On sentences provable in fragments of bounded arithmetic
abstract: Bounded arithmetic refers to the system of relatively weak subsystems of Peano Arithmetic that are loosely connected with complexity classes studied in computational complexity. Typically, the induction schema is restricted to a class of formulas that define a particular complexity class and provably total functions (defined by a suitably restricted class of formulas) are functions computable in a particular complexity class. The basic problem studied in bounded arithmetic is similar to the problems in computational complexity: to prove separations of theories, i.e., to prove that one theory is stronger (or non conservative over a given class of formulas) than another one. As in computational complexity, these problems do not seem to be amenable to current mathematical methods. Nevertheless, by giving combinatorial characterization of sentences provable in the studied theories we can, at least, get some partial evidence for our conjectures about which theories are stronger. Combinatorial characterization of provable ∀Σ1b sentences have been obtained for the main first order fragments T2i and two second order fragments U21 and V21. In this lecture we will present an approach which possibly may lead to characterizations of such sentences in the (probably) stronger fragments V2i, for i ≥ 2.
- Alexis Bes (University of Paris 12)
title: Decidability of fragments of arithmetic
abstract: The study of decidability of fragments of arithmetic is a classical topic in logic, which was initiated by Tarski, Skolem and Presburger in the 1920s. Two of the most important results in this field are Presburger’s proof of the decidability of arithmetic without multiplication, and Matiyasevich-Davis-Robinson-Putnam’s proof of the undecidability of the existential theory of arithmetic (which provides a negative solution to Hilbert’s tenth problem). In this talk, we survey important results and problems in the field, with a focus on the decidable side. In particular, we discuss methods for proving decidability, connections with open problems in number theory, connections between (expansions of) Presburger arithmetic and automata and combinatorics over words, as well as implementation of decision procedures and complexity issues.
- Leszek Kolodziejczyk (University of Warsaw)
title: Two frontier problems in bounded arithmetic
abstract: In the mid-1990s, asking an expert “What are the problems on the frontier of research in bounded arithmetic?” would have plausibly led to an answer along the lines of “There are two such problems: (i) separating the relativized bounded arithmetic hierarchy by sentences of fixed quantifier complexity, and (ii) proving a combinatorial independence result for relativized bounded arithmetic with an additional quantifier for counting mod 2”. Today, the answer could very well be the same! In my talk, I plan to discuss these two frontier problems and explain what we have learned in the last two decades.
- Albert Visser (University of Utrecht)

