Brusselator
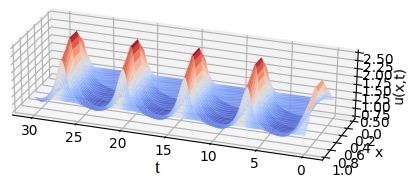
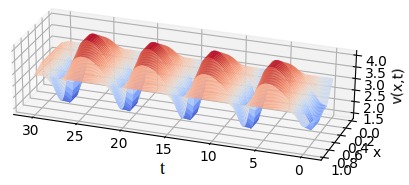
We consider the 1D Brusselator partial differential equation (PDE). Here we consider a state of the form \(x(y,t)=(u(y,t),v(y,t))\) where \(y\in \Omega = [0,\ell]\) is the spatial location. The PDE is of the form:
\begin{cases} \frac{\partial u}{\partial t} = A+u^2v-(B+1)u+\sigma \nabla^2 u\\ \frac{\partial v}{\partial t} = Bu-u^2v+\sigma \nabla^2 v \end{cases}
with boundary condition: \(u(0,t)=u(\ell,t)=1\), \(v(0,t)=v(\ell,t)=3\), and initial condition \(x_0(y)=(u(y,0),v(y,0))\) with: \(u(y,0)=1+sin(2\pi y)\), \(v(y,0)=3\).
Results Source codeReadme