Biochemical process
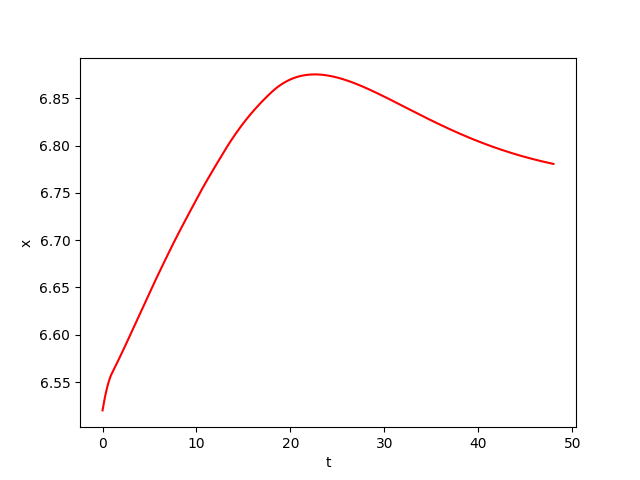
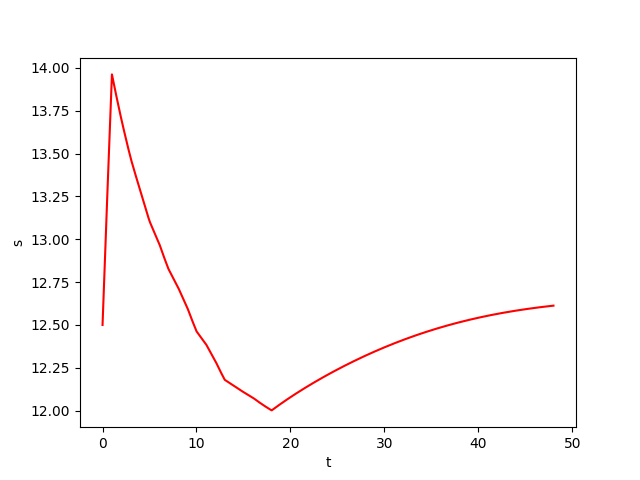
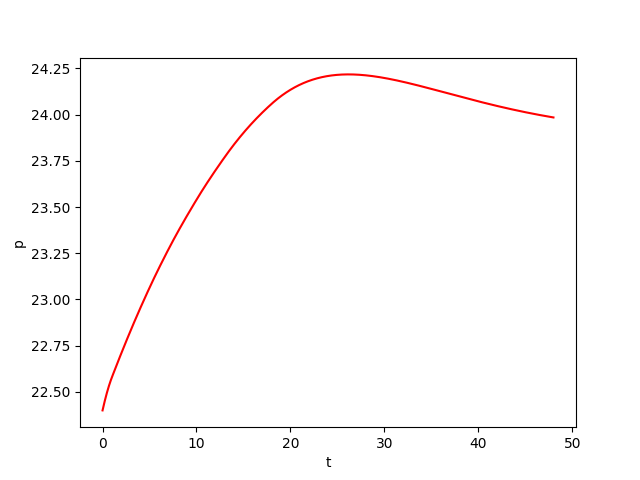
We consider a biochemical process model \(Y\) of continuous culture fermentation. Let \(Y = (X, S, P) \in \mathbb{R}^3\) satisfies the differential system: \begin{equation*} \begin{cases} \overset{.}{X}(t) = -D X(t) + \mu(t) X(t)\\ \overset{.}{S}(t) = D \big( S_f(t) - S(t) \big) - \frac{\mu(t)X(t)}{Y_{x/s}}\\ \overset{.}{P}(t) = -D P + \big( \alpha\mu(t) + \beta \big) X(t)\\ \end{cases} \end{equation*} where \(X\) denotes the biomass concentration, \(S\) the substrate concentration, and \(P\) the product concentration of a continuous fermentation process. The model is controlled by \(S_f \in [S_f^\mathit{min}, S_f^\mathit{max}]\). While the dilution rate \(D\), the biomass yield \(Y_{x/s}\) , and the product yield parameters \(\alpha\) and \(\beta\) are assumed to be constant and thus independent of the actual operating condition, the specific growth rate \(\mu : \mathbb{R} \rightarrow \mathbb{R}\) of the biomass is a function of the states:\begin{equation*} \mu(t) = \mu_m\frac{\left( 1-\frac{P(t)}{P_m}\right) S(t)}{K_m + S(t)+\frac{S(t)^2}{K_i}} \end{equation*}
The goal is to maximize the average productivity presented by the cost function:\begin{equation*} J_k = \frac{1}{T}\int^T_0DP(t)dt \end{equation*}
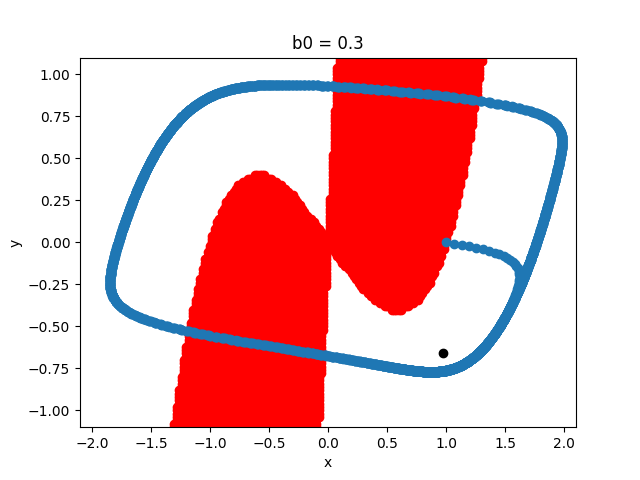
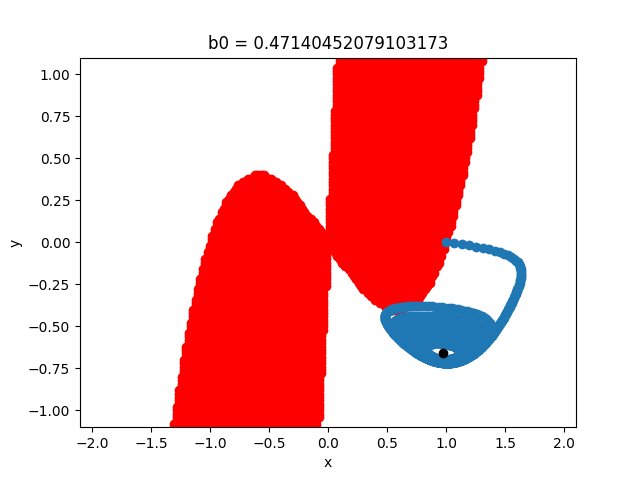
Results Source code Readme