MathStic Category Theory Workshop
Date : June 16, 2025
Place : Amphi Copernic, institut Galilée, Sorbonne Paris Nord, Villetaneuse
Access
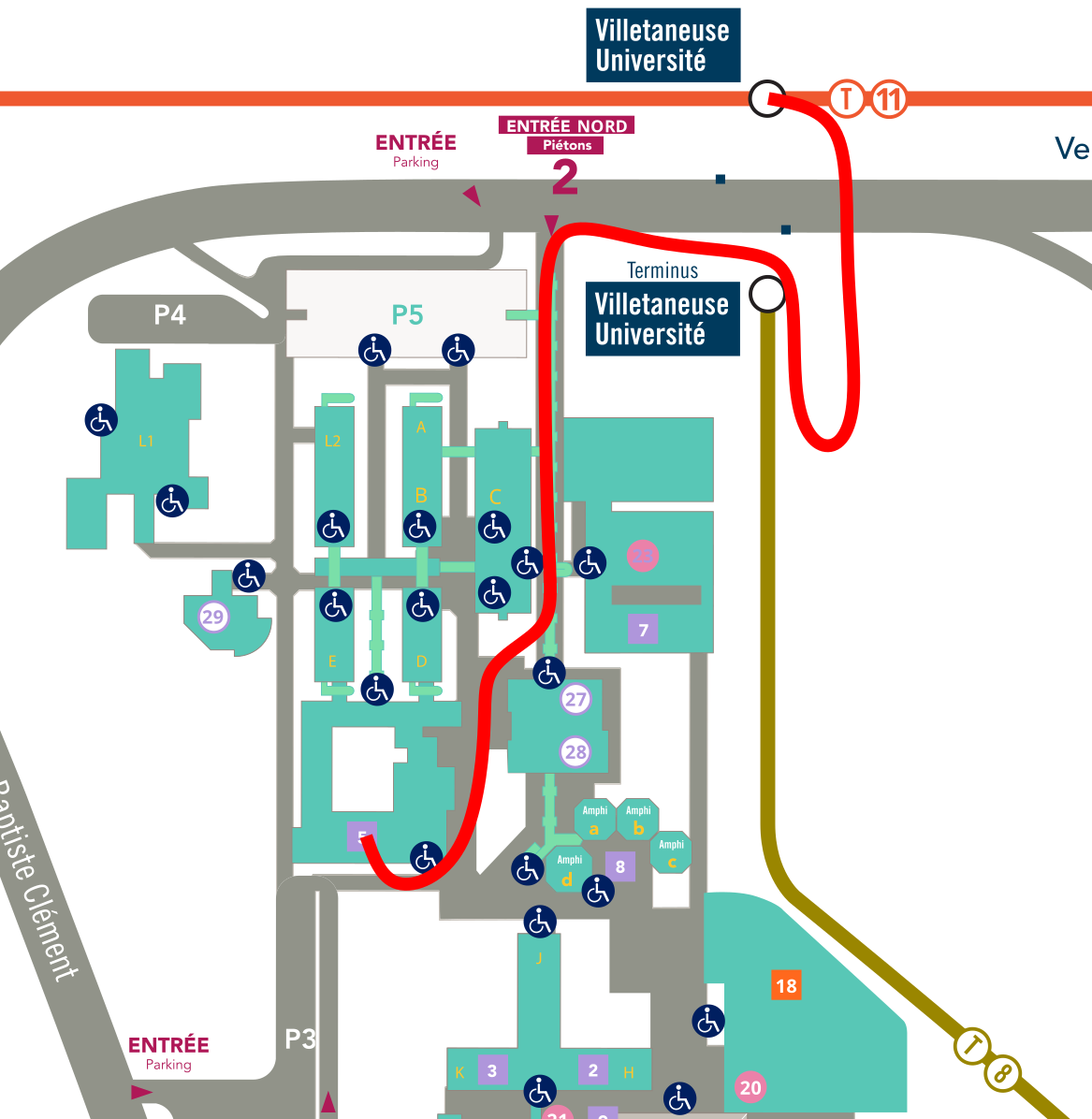
Station "Villetaneuse-université" on Tramway T11, which connects to lines B, C, D and H, and on Tramway T8 which connects to line 13 and Tramway T1. Due to civil works (for our future building !), the entrance of the university keep switching places, in June, the entrance should be at the north of the university, as shown in the map bellow. The amphitheatre (Copernic) is accessible while following the map without taking any stair (except those of the T11 station); which is much easier than accessing the lab for those that would have a bad experience of it.
Speakers :
- Sacha Ikonicoff
- Jad Koleilat
- Samuel Mimram
-
Paige North (annulation)
- Paula Verdugo
Program :
Abstracts :
- Jad Koleilat, An Introduction to Categorical Semantics : Formulas as Objects and Proofs as Morphisms
This talk is an introduction to categorical semantics aimed at non-logicians. We introduce
formal proofs systems, explaining intuitions and giving examples. We then explain how we can interpret these
structures as categories. We give the classical example of cartesian closed categories and finish with examples
relating to functional analysis.
- Samuel Mimram, Type theoretic definitions of structured weak higher categories
Weak higher categories generalize the traditional notion of category by comprising higher-dimensional cells and using those in order to provide witnesses for structural axioms. Due to their very general nature, they are difficult to manipulate and even to define. In this talk, I present a type theoretic approach for defining weak globular categories in the sense of Grothendieck and Maltsiniotis, which gives rise to a tool to mechanically check the existence of structural cells. I also present some recent extensions of this work in order to define weak categories with structure. In particular, I define weak cartesian closed categories, and explain how this corresponds to an unbiased notion of λ-calculus.
- Paula Verdugo, On the equivalence invariance of formal category theory
Equipments, a special kind of double categories, have shown to be a powerful environment to express formal category theory. We build a model structure on the category of double categories and double functors whose fibrant objects are the equipments, and combine this together with Makkai’s early approach to equivalence invariant statements in higher category theory via FOLDS (First Order Logic with Dependent Sorts) and Henry’s recent connection between model structures and formal languages, to show a result on the equivalence invariance of formal category theory.
- Sacha Ikonicoff, Gradient descent and neural networks: a categorical approach
A neural network can be thought of as a mathematical gadget which can compute a prediction from a list of inputs, using mostly parametrised linear maps. To find the right parameters and "calibrate" the neural network, one uses a technique called deep learning. Given a set of observation data, one can compute the error, i.e., the distance between the prediction given by the neural network and the observed consequence. Deep learning then uses gradient descent to update the parameters in a way which will reduce the error. This updating process is called backpropagation.
In recent years, category theorists have developed a framework to study and generalise gradient descent and neural networks. There is a construction called Para which categorises the notion of parametrised function, and a construction called Optic (a generalisation of former constructions such as Learners and Lenses), which formalises a notion of backpropagation. In this framework, neural networks are seen as maps in a small category NNet, Gradient Descent is seen as a functor from Para to Para (Optic), and deep learning can then be defined as a composition of a functor from NNet to Para with Gradient Descent.
In this talk, I will present all these notions, as well as a notion of Deep Dreaming which comes from the optic construction. These correspond to work of Fong--Spivak--Tuyeras, Cruttwell--Gavranović--Ghani--Wilson--Zanasi and Capucci--Gavranović--Hedges--Rischel. Time permitting, I will also present a generalisation of the backpropagation functor using notions from Cartesian Differential Categories, due to Cockett--Cruttwell--Gallagher--Lemay--MacAdam--Plotkin--Pronk.


.