



Next: Fonction de Weierstrass et
Up: Réciprocité dans un corps
Previous: Réciprocité dans un corps
L'article Loi de réciprocité dans les corps quadratiques imaginaires,
Annales de l'Institut Fourier, 1995, de A. Bayad,
nous donne, dans un tel corps  :
:
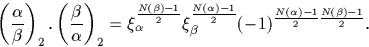
Dans les précisions suivantes 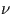 désigne à la fois α et β , des entiers algébriques.
désigne à la fois α et β , des entiers algébriques. 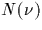 désigne la norme de
désigne la norme de 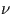 dans
dans 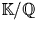 .
.
Rappel sur l'anneau 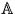 des entiers de
des entiers de 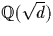 :
:
si ![$d \equiv 1 \ [4]$](img309.gif) alors
alors
![\begin{displaymath}
{\mathbb A}={\mathbb Z}[\frac{1+\sqrt{d}}{ 2}]=\{\frac{u+v \sqrt{d} }{2} \ \vert \ u,v \in {\mathbb Z}, u\equiv v \ [2] \}\end{displaymath}](img310.gif)
et le discriminant est donné par 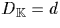 ;
;
si ![$d\equiv 2,3 \ [4]$](img312.gif) alors
alors
![\begin{displaymath}
{\mathbb A}={\mathbb Z}[\sqrt{d}]={\mathbb Z}+\sqrt{d}{\mathbb Z}\end{displaymath}](img313.gif)
et le discriminant
est donné par 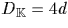 .
.
Cyril Banderier
7/23/1997
![]()
![]() des entiers de
des entiers de ![]() :
:
![]() alors
alors
![]()
![]()