



Next: Lemme sur la somme
Up: Quelques démonstrations de la
Previous: Un petit théorème de
Parmi les nombreuses démonstrations de la loi de réciprocité, il en est
qui utilisent les corps finis. En voici donc une seconde, une tirée
de [Naudin]. On considère un sur-corps 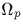 de
de 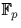 contenant une
racine
contenant une
racine 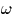 de l'unité, d'ordre q.
On introduit la somme de Gauss :
de l'unité, d'ordre q.
On introduit la somme de Gauss :
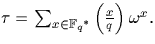 Gauss les a utilisées pour sa sixième (1808) et huitième (1818) preuve
de la loi de réciprocité.
On remarquera, puisque
Gauss les a utilisées pour sa sixième (1808) et huitième (1818) preuve
de la loi de réciprocité.
On remarquera, puisque 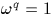 , que
, que 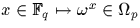 est bien définie et vérifie
est bien définie et vérifie 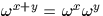 .
Dans le corps
.
Dans le corps 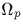 ,
,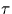 est une racine carrée de
est une racine carrée de 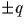 , comme le montre le lemme suivant.
, comme le montre le lemme suivant.
Cyril Banderier
7/23/1997