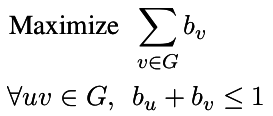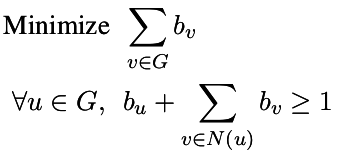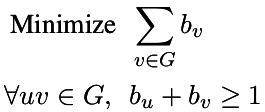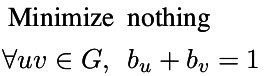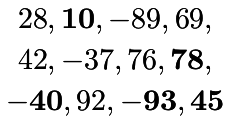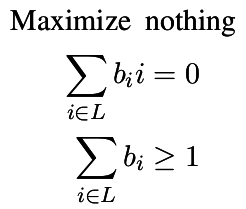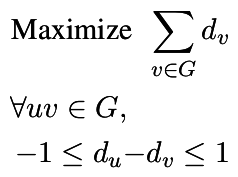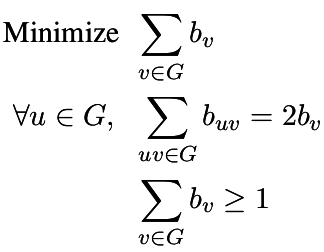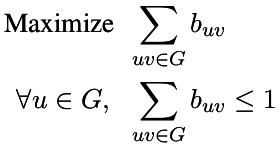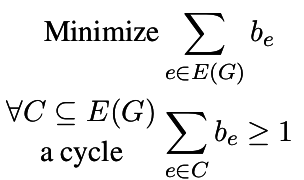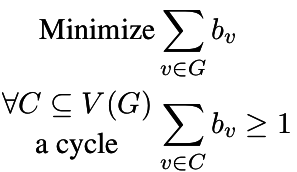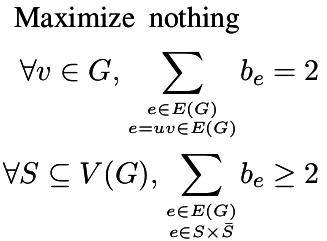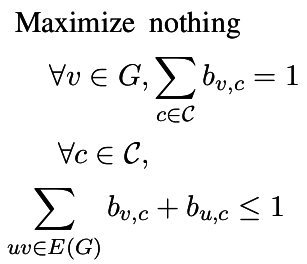| Independent Set |
| Maximum set of pairwise non-adjacent vertices in a graph |
 |
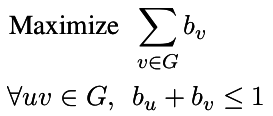 |
p = MixedIntegerLinearProgram(maximization = True)
b = p.new_variable(binary = True)
p.set_objective( sum([b[v] for v in g]) )
for u,v in g.edges(labels = False):
p.add_constraint( b[u] + b[v] <= 1 )
p.solve()
b = p.get_values(b)
print [v for v,i in b.items() if i]
|
| Dominating Set |
| Minimum set of vertices whose neighborhood is the whole graph |
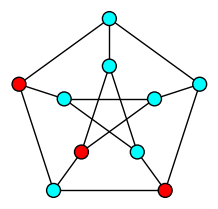 |
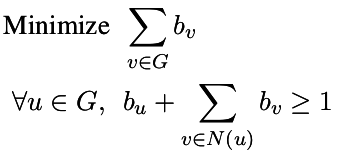 |
p = MixedIntegerLinearProgram(maximization = False)
b = p.new_variable(binary = True)
p.set_objective( sum([b[v] for v in g]) )
for u in g:
p.add_constraint( b[u] + sum([b[v] for v in g.neighbors(u)]) >= 1 )
p.solve()
b = p.get_values(b)
print [v for v,i in b.items() if i]
|
| Vertex Cover |
| Minimum Set of vertices touching each edge |
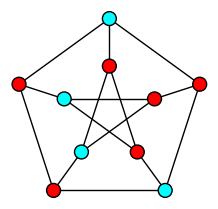 |
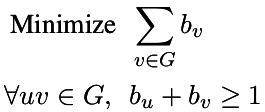 |
p = MixedIntegerLinearProgram(maximization = False)
b = p.new_variable(binary = True)
p.set_objective( sum([b[v] for v in g]) )
for u,v in g.edges(labels = False):
p.add_constraint( b[u] + b[v] >= 1 )
p.solve()
b = p.get_values(b)
print [v for v,i in b.items() if i]
|
| Partition |
| Partition a set of integers into two sets whose sum is equal |
 |
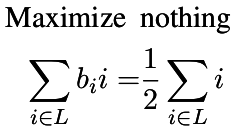 |
l = [82, 61, 56, 44, 28, 87, 90, 36, 11, 48, 9]
p = MixedIntegerLinearProgram()
b = p.new_variable(binary = True)
p.add_constraint(p.sum([ v*b[v] for v in l ]) == sum(l)/2)
p.solve()
b = p.get_values(b)
print [v for v in b if b[v] == 1]
|
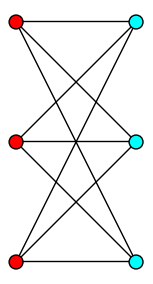
| Bipartite Set |
| Partition the graph into two independent sets |
 |
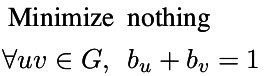 |
p = MixedIntegerLinearProgram()
b = p.new_variable(binary = True)
for u,v in g.edges(labels = False):
p.add_constraint( b[u] + b[v] == 1 )
p.solve()
b = p.get_values(b)
print [v for v,i in b.items() if i]
print [v for v,i in b.items() if not i]
|
| Subset Sum |
| Find a nonempty subset of integers with null sum |
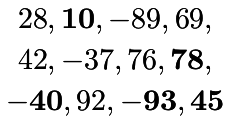 |
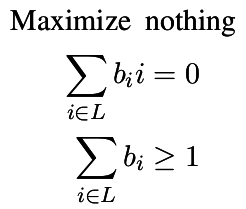 |
l = [28, 10, -89, 69, 42, -37, 76, 78, -40, 92, -93, 45]
p = MixedIntegerLinearProgram()
b = p.new_variable(binary = True)
p.add_constraint(p.sum([ v*b[v] for v in l ]) == 0)
p.add_constraint(p.sum([ b[v] for v in l ]) >= 1)
p.solve()
b = p.get_values(b)
print [v for v in b if b[v] == 1]
|
| Distances |
| Compute the distance from vertex 0 to any other |
 |
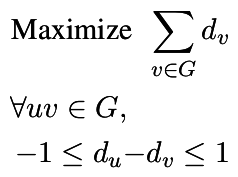 |
p = MixedIntegerLinearProgram()
d = p.new_variable()
p.set_objective(sum([d[v] for v in g]))
p.add_constraint( d[0] == 0 )
for u,v in g.edges(labels = False):
p.add_constraint( -1 <= d[u] - d[v] <= 1 )
p.solve()
print p.get_values(d)
|
| Girth |
| Size of the shortest cycle |
 |
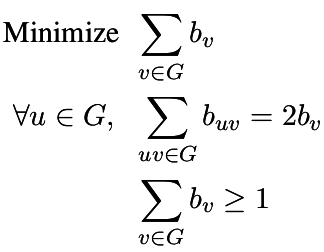 |
p = MixedIntegerLinearProgram(maximization = False)
b = p.new_variable(binary = True)
p.set_objective(sum([b[v] for v in g]))
p.add_constraint(sum([b[v] for v in g]) >= 1)
for v in g:
edges = g.edges_incident(v, labels = False)
p.add_constraint( sum([b[Set([e])] for e in edges]) == 2*b[v] )
p.solve()
b = p.get_values(b)
print [v for v in g if b[v]]
|
| Matching |
| Maximum number of non-incident edges |
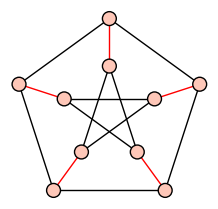 |
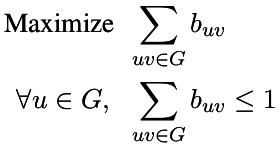 |
p = MixedIntegerLinearProgram(maximization = True)
b = p.new_variable(binary = True)
p.set_objective(sum([b[Set(e)] for e in g.edges(labels = False)]))
for v in g:
edges = g.edges_incident(v, labels = False)
p.add_constraint( sum([b[Set(e)] for e in edges]) <= 1 )
p.solve()
b = p.get_values(b)
print [e for e,i in b.items() if i]
|
| Feedback Arc Set |
| Minimum set of arcs hitting all circuits |
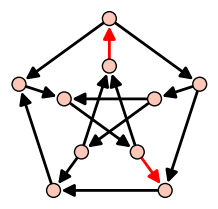 |
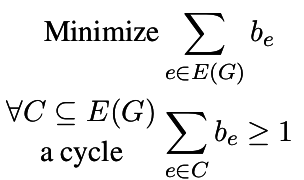 |
p = MixedIntegerLinearProgram(maximization = False)
b = p.new_variable(binary = True)
p.set_objective(sum([b[u,v] for u,v in g.edges(labels = False)]))
p.solve()
while True:
b_sol = p.get_values(b)
g_tmp = DiGraph()
g_tmp.add_edges([e for e,i in b_sol.items() if i==0])
isok, C = g_tmp.is_directed_acyclic(certificate = True)
if isok:
break
edges = zip(C, C[1:]+[C[0]])
p.add_constraint(sum([b[e] for e in edges])>= 1)
p.solve()
print [e for e,i in b_sol.items() if i==1]
|
| Feedback Vertex Set |
| Minimum set of vertices hitting all circuits |
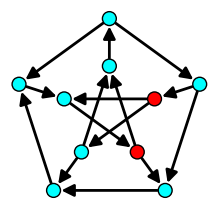 |
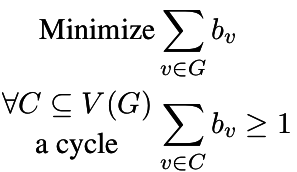 |
p = MixedIntegerLinearProgram(maximization = False)
b = p.new_variable(binary = True)
p.set_objective(sum([b[v] for v in g]))
p.solve()
while True:
b_sol = p.get_values(b)
vertices = [v for v,i in b_sol.items() if i==0]
g_tmp = g.subgraph(vertices = vertices)
isok, C = g_tmp.is_directed_acyclic(certificate = True)
if isok:
break
p.add_constraint(sum([b[v] for v in C])>= 1)
p.solve()
print [e for e,i in b_sol.items() if i==1]
|
| Hamiltonian Cycle |
| A cycle going through all vertices |
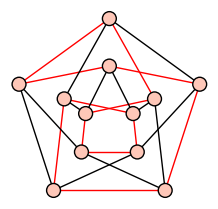 |
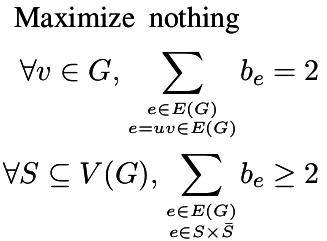 |
p = MixedIntegerLinearProgram()
b = p.new_variable(binary = True)
for v in g:
edges = g.edges_incident(v, labels = False)
p.add_constraint( sum(b[Set(e)] for e in edges) == 2)
p.solve()
while True:
b_sol = p.get_values(b)
edges = [e for e,i in b_sol.items() if i == 1]
g_tmp = g.subgraph(vertices = g.vertices(), edges = edges)
cc = g_tmp.connected_components()
if len(cc) == 1:
break
boundary = g.edge_boundary(cc[0], labels = False)
p.add_constraint(sum([b[Set(e)] for e in boundary])>= 2)
p.solve()
print g_tmp.edges(labels = False)
|
| 3-coloration |
| Partition a graph into three independent sets |
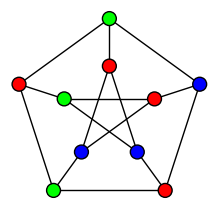 |
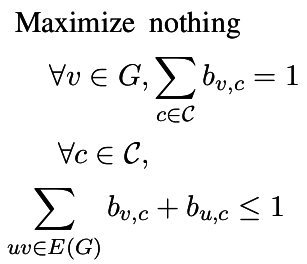 |
p = MixedIntegerLinearProgram()
b = p.new_variable(binary = True)
for v in g:
p.add_constraint( b[v,0] + b[v,1] + b[v,2] == 1 )
for u,v in g.edges(labels = False):
p.add_constraint( b[u,0] + b[v,0] <= 1 )
p.add_constraint( b[u,1] + b[v,1] <= 1 )
p.add_constraint( b[u,2] + b[v,2] <= 1 )
p.solve()
b = p.get_values(b)
print [v for (v,c),i in b.items() if i and c == 0]
print [v for (v,c),i in b.items() if i and c == 1]
print [v for (v,c),i in b.items() if i and c == 2]
|