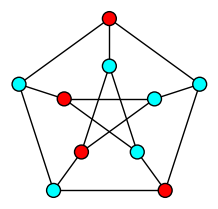
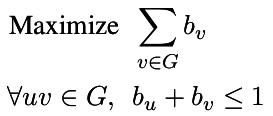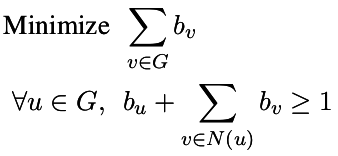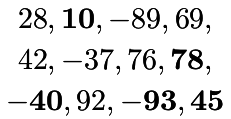| Independent Set |
| Maximum set of pairwise non-adjacent vertices in a graph |
 |
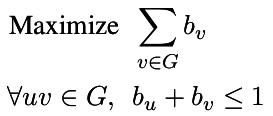 |
p = MixedIntegerLinearProgram(maximization = True)
b = p.new_variable(binary = True)
p.set_objective( sum([b[v] for v in g]) )
for u,v in g.edges(labels = False):
p.add_constraint( b[u] + b[v] <= 1 )
p.solve()
b = p.get_values(b)
print [v for v,i in b.items() if i]
|
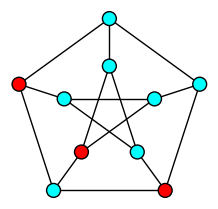
| Dominating Set |
| Minimum set of vertices whose neighborhood is the whole graph |
 |
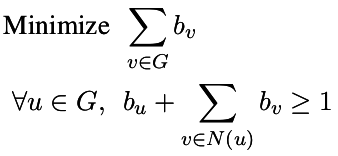 |
|
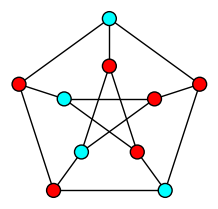
| Vertex Cover |
| Minimum Set of vertices touching each edge |
 |
|
|
| Partition |
| Partition a set of integers into two sets whose sum is equal |
 |
|
|
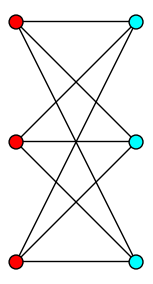
| Bipartite Set |
| Partition the graph into two independent sets |
 |
|
|
| Subset Sum |
| Find a nonempty subset of integers with null sum |
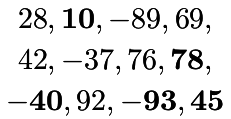 |
|
|
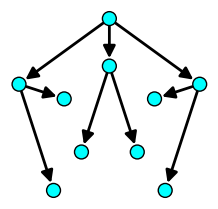
| Distances |
| Compute the distance from vertex 0 to any other |
 |
|
|
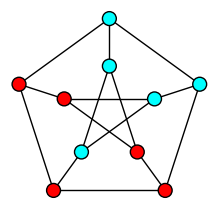
| Girth |
| Size of the shortest cycle |
 |
|
|
| Matching |
| Maximum number of non-incident edges |
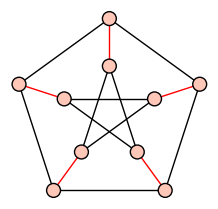 |
|
|
| Feedback Arc Set |
| Minimum set of arcs hitting all circuits |
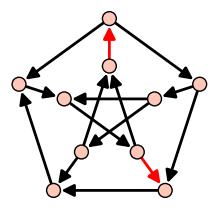 |
|
|
| Feedback Vertex Set |
| Minimum set of vertices hitting all circuits |
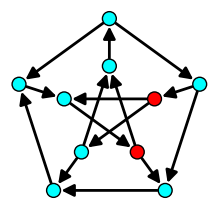 |
|
|
| Hamiltonian Cycle |
| A cycle going through all vertices |
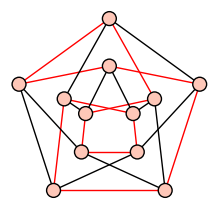 |
|
|
| 3-coloration |
| Partition a graph into three independent sets |
 |
|
|