You can find here pictures or videos related to my research, sometimes with comments (most of the pictures are resized: right click on them to show them in real size).
A (classical) soccer ball is made of 12 pentagons and 20 hexagons.
No two pentagons are adjacent, and one can show that this constraint suffices to characterize the classical ball.
What if we relax it?
Then we can get different balls.
These are specific fullerenes or buckyballs, and there are 1812 different ones.
The picture below shows three of them that I assembled with real parts of soccer balls (you can even try to play with).
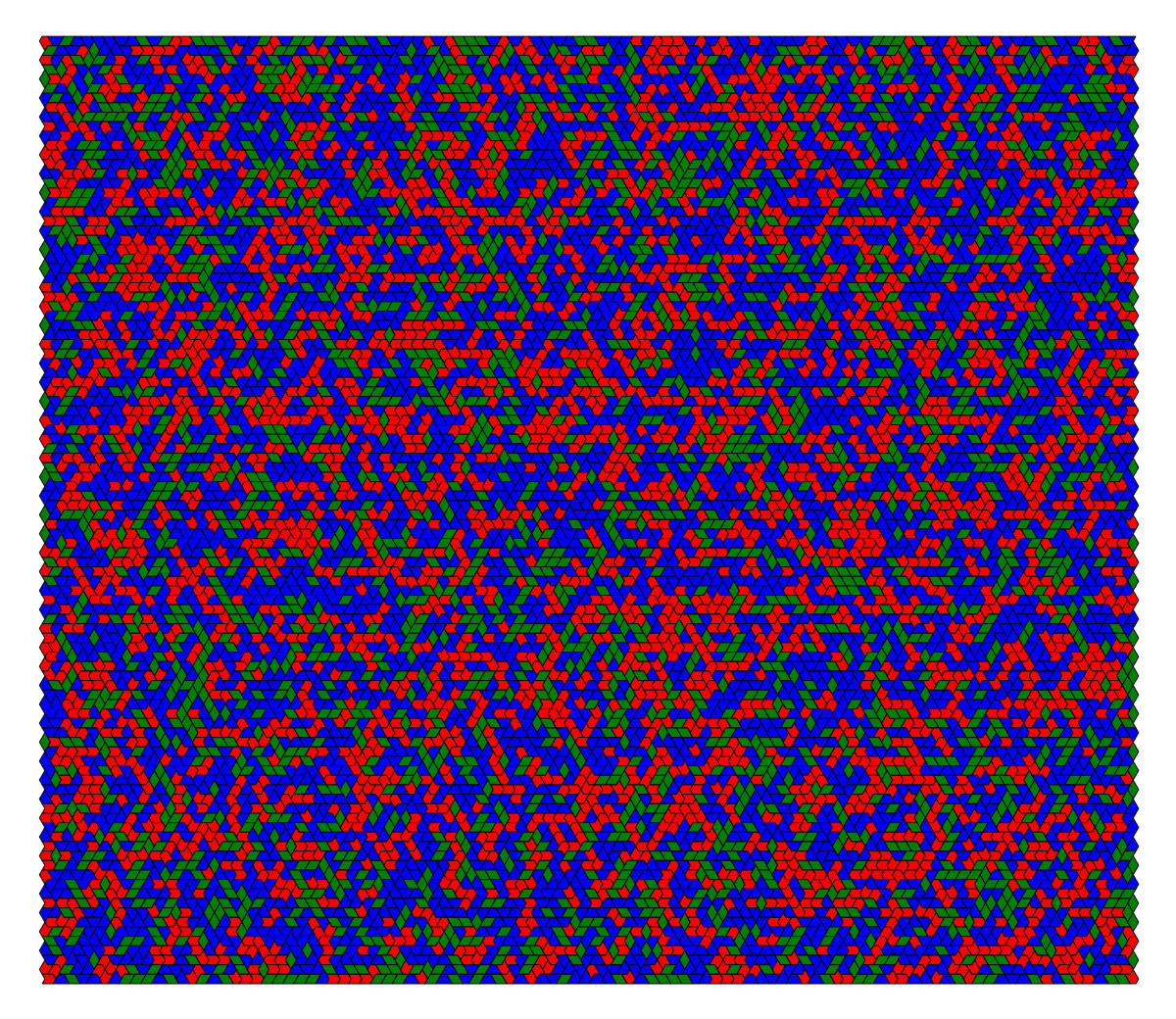
Continuous transformation between binary disc packings with a triangulated contact graph, designed to break as few contacts as possible.
You can spot (can you?) 7 of the 9 binary disc packings depicted here.
The steps are laser-cut from MDF and glued together like a dome (there are supporting arches underneath).
One filling is uniformly randomly drawn for each size (10, 20, 30, 40 and 70 small cubes on each side), the other is the complementary filling (which allows them to be combined to make a cube that is easy to transport).
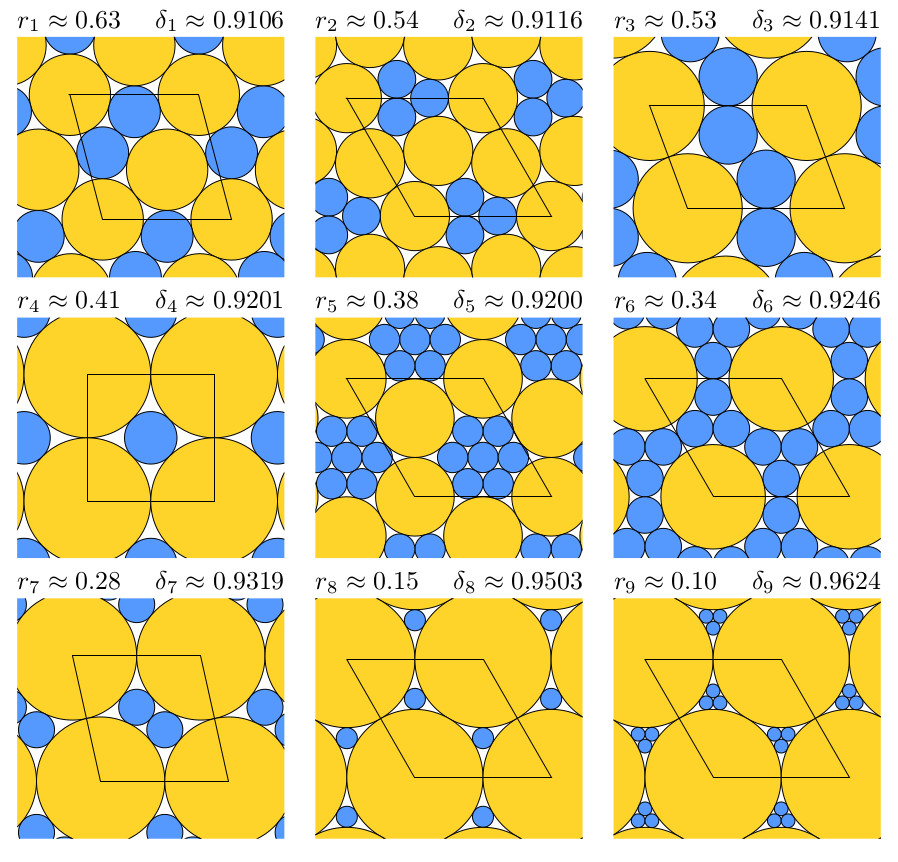
Everyone knows the best way to arrange identical coins on a table, without overlapping, so as to minimize the area left free between the coins. This is the hexagonal compact packing: the coins are centred on a triangular grid. What if there are two different coins? More?
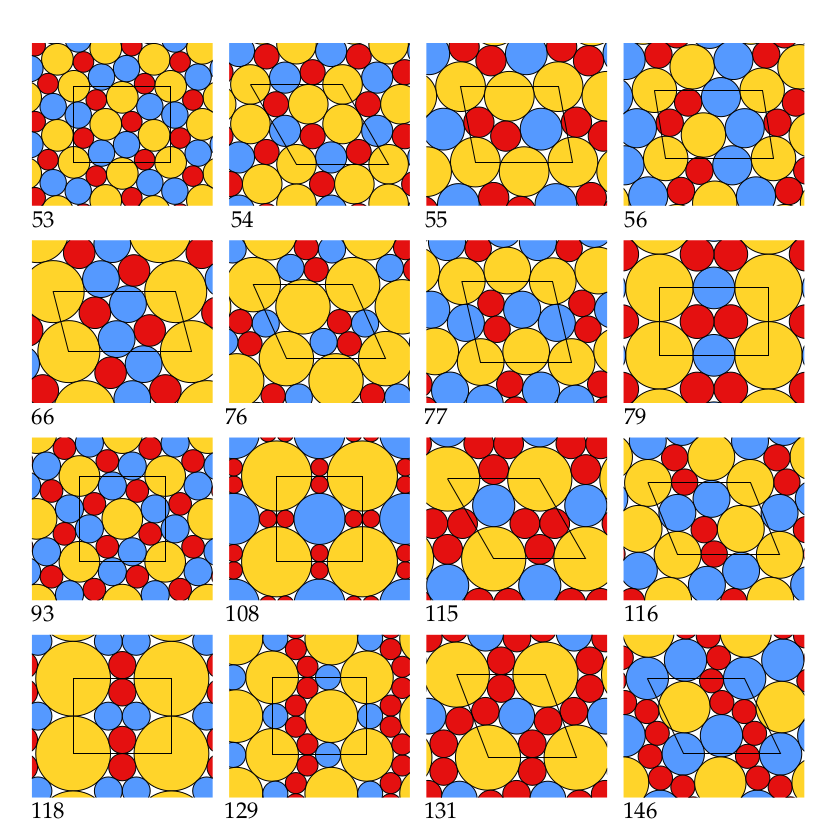
Some coin size ratios are particular: they allow to have only "triangular" spaces between the coins: this is called compact or triangulated packing. There are only 9 ratios of two coins allowing this. There are also 164 triplets of sizes allowing compact packing (full list, exact radii and applet to play with).
For each of the 9 ratios which allow a binary triangulated packing, the density has been shown to be maximized by such a packing. This also holds for 16 of the 164 cases of ternary triangulated packings. These are the packings depicted above.
 |
 |
| Packings which maximize the density, for each ratio which allow a binary triangulated packing. |
Packings which maximize the density, for 16 of the 164 ratios which allow a ternsary triangulated packing. |
These patterns also seem to appear in this simulation of the assembly of nanoparticles on a diethylene glycol " ice rink " (common work with chemists of the LPCNO).
Consider the tilings of a grid by two squares, respectively of side 1 and c>1 (for c=2 this is related to the king problem, and close to the fibonacci 2D subshift problem). How many are them? How to efficiently random sample one of them? For which value of c does a typical tiling contains the more small squares (i.e., which of the below pictures is the whitest one)? What about random tilings by squares of any size?
 |
 |
 |
 |
 |
 |
| Sides 1 and 2 |
Sides 1 and 3 |
Sides 1 and 4 |
Sides 1 and 5 |
Sides 1 and 6 |
Integer sides |
A wood parquet (pine & oak) that I made in november 2015. More photos and details there (in french).
On the trihexagonal lattice, also called kagome lattice, consider the tiles formed by gluing two triangles to each hexagon. This is a sort of "trimer tiling", which nevertheless admits a height function (i.e. can be seen as a surface in the Euclidean space). Such tilings can be sampled by coupling from the past, but what about the mixing rate? There is also arctic-circle-like phenomena.
The arctic circle phenomenon is well known for dimer tilings, aka rhombus tilings of codimension one. The same phenomenon seems appearing in higher codimensions.
 |
 |
 |
| Codimension 1 |
Codimension 2 |
Codimension 3 |
Shrinking three of the five vectors defining the rhombi of a Penrose tiling yields a periodic tiling (there is ten ways to do this, see left video). This is because in each stripe the fat rhombi alternate in two orientations, and the same for thin rhombi. The tilings which satisfy this alternation condition are the so-called generalized Penrose tiling (right video).
|
|
|
The Beenker tilings are the tilings by a square and a 45° rhombus such that any two rhombi, either adjacent or connected by a line made of squares, have different orientations. They can all be seen as digitization of a one-parameter family of planes in the four dimensional space. The tilings which minimize the proportion of squares are aperiodic: they are indeed the Ammann-Beenker tilings! Using the parameter as time yields the video below.
|
|
|
|
| Typical tiling |
Maximal tiling |
Concentric rings |
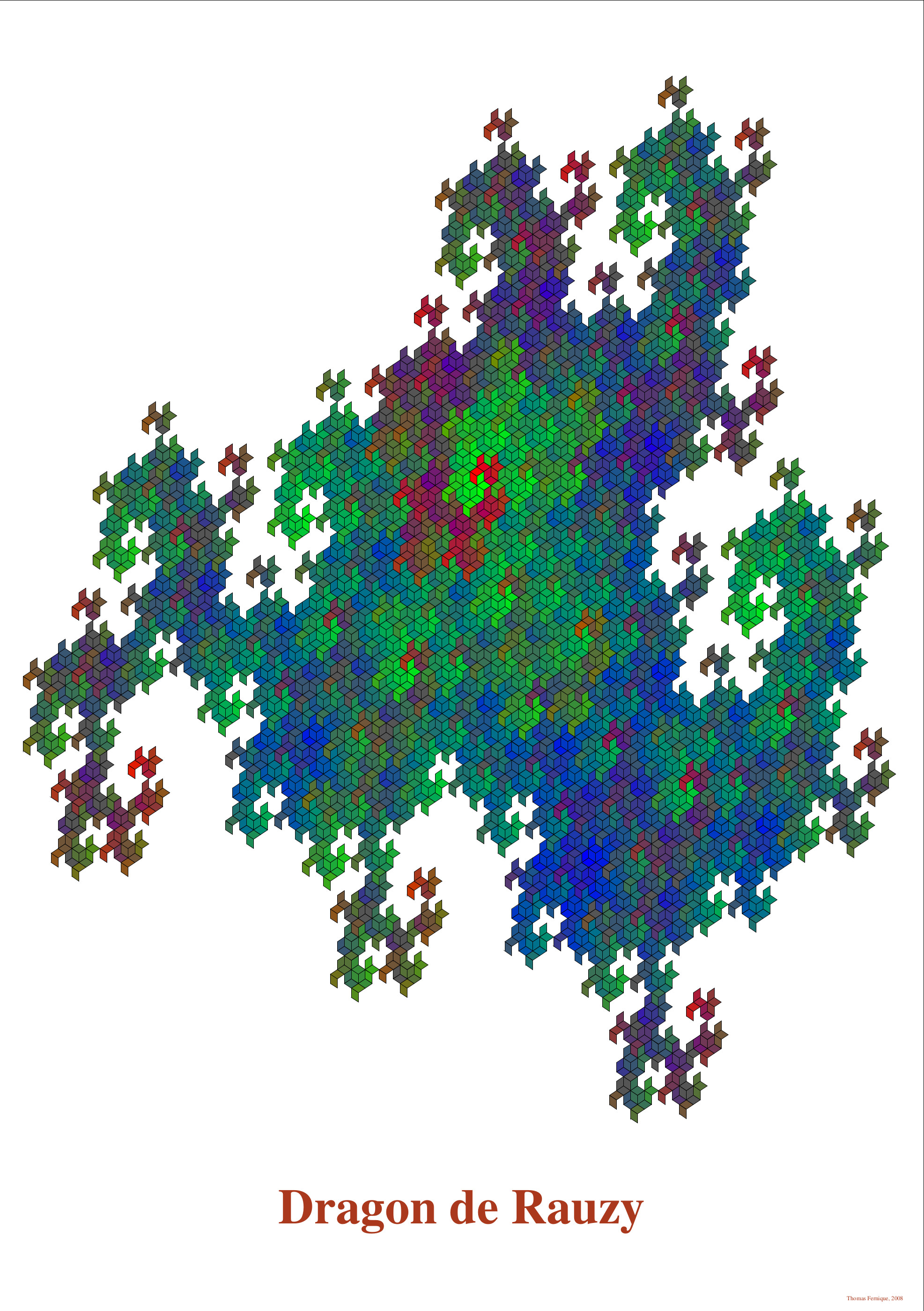
Rauzy's dragon
A pattern obtained by iterated applications of a generalized substitution à la Arnoux-Ito on an initial pattern made of three tiles. Colors encode (in RGB) the ancestry of each tile (the three initial tiles are pure blue, green and red).
Some posters which I drew for conferences that I co-organized.
 |
 |
 |
 |
| Math-Info 2010 |
Allouche's 60th birthday |
Tilings and Tesselations |
TransTile |
