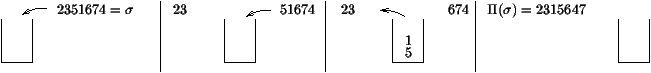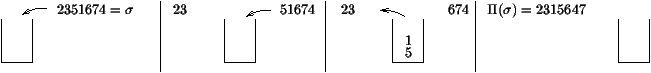Sorted and/or Sortable Permutations
Mireille Bousquet-Mélou
LaBRI, Université de Bordeaux
Algorithms Seminar
June 8, 1998
[summary by
Cyril Banderier]
A properly typeset version of this document is available in
postscript and in
pdf.
If some fonts do not look right on your screen, this might be
fixed by configuring your browser (see the documentation here).
1 Introduction
The classical railroad cars switching problem [12] (viz.
to reorder cars in a given order with the help of a single garage-track)
is here revisited and generalised in terms of permutations and trees.
Permutations which are sortable by one (or more than one) stack
have been studied by West [14] and some generating functions have been
found [15]. By factorising
permutations (following and generalising an idea of Zeilberger's),
Mireille Bousquet-Mélou obtained functional equations for one-stack sortable,
two-stack sortable, sorted permutations, sorted and sortable permutations.
She shows q-analogues arise in counting inversions.
Most of these functional equations involve divided differences.
The quadratic method allows to solve some of them while the other ones
remain quite mysterious. She also gives an algorithm which
decides if a permutation is sorted.
2 Sorting Procedure
In his Ph.D. thesis [14], Julian West studied a
procedure P that permutes the letters of a word s
consisting of distinct
letters in the alphabet {1,2,3, ... }.
The procedure uses a stack s and works as follows:
-
t:=e
- s:=e
- while s¹ e do
-
f:=Firstletter(s)
- if s=e or f<Top(s)
- end
- t:=ts~
- return t
In this procedure, e is the empty word, s~ is the
mirror of the word s and the inverse b-1 of a letter b of
the alphabet
{1,2,3, ... } is a new letter with the property
b b-1=b-1 b = e.
The output word t has n letters, and we define
it to be P(s), the word obtained by sorting s
through a stack.
This procedure extends a procedure described by Knuth
[12, p. 238].
West observed that the map P can alternatively be
described recursively by P (sL m sR)
=P(sL)P (sR)m
where m is the largest letter of
the word s = sL m sR.
With at most n-1 iterations, s is an increasing word, i.e.
P sorts the letters of s.
Figure 1: The sorting algorithm applied to s=2351674.
Let Sn be the set of permutations of {1,2,...,n}.
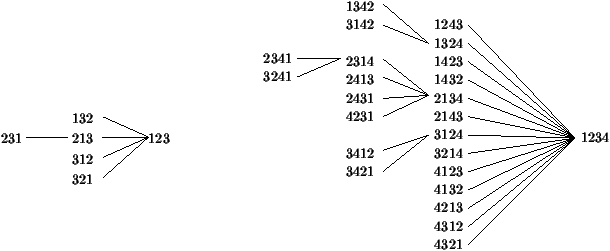
We represent the action of P on Sn by a sorting tree: the nodes of this tree are the elements of Sn, and
an edge connects s to P(s) for all s Î Sn.
Figure 2: The sorting trees for S3 and S4.
We can visualise on this tree the four classes of permutations
we will consider in this paper.
One-stack sortable permutations
These permutations occur
in the last two columns of the sorting
tree. Knuth [12] proved that the number of such permutations is binomial(2n,n)/(n+1).
They are exactly the permutations avoiding the pattern 231: there
exists no triple (i,j,k) with 1£ i<j<k£ n such that
s(k)<s(i)<s(j).
Two-stack sortable permutations
They occur in the last three
columns of the sorting tree. Their generating function å cn xn satisfies
x2F3+x(2+3x)F2+(1-14x+3x2)F+x2+11x-1=0.
West conjectured that
This was proved by Zeilberger [15],
who found the previous equation and then used the Lagrange inversion formula.
Sorted permutations
These are those permutations which belong to
P( Sn).
Induction on the length of permutations shows that
any suffix of a sorted permutation is a sorted word.
Sorted permutations cannot be described in terms of
forbidden patterns: in fact any pattern occurs as a factor in some
sorted permutation.
We shall give a functional
equation satisfied by their generating function.
Sorted and (one-stack) sortable permutations
Their generating function satisfies
x3 F4+x2(3+4x)F3+x(3-29x+6x2)F2+(1-7x+29x2+4x3)F-(1-x)3=0.
3 Permutations and Trees
There is a classical bijection between permutations and binary search trees:
one gets a permutation from a labelled tree by reading it with a
``lower reading'' (you start at the root, and recursively, you read the
subtrees, the left one at first, and when you have visited all the left
children, you add the label of the current node to a list, the final list
is the permutation associated to the tree),
on the other hand
one gets a tree from a permutation s=sL m sR by
creating recursively the tree with root m and
a left subtree associated to sL
and a right subtree associated to sR.
We will now show on an example an algorithm that decides whether a
permutation is sorted and, if it is indeed sorted, gives the pre-image.
Beginning with t = 6.3.11.1.4.5.2.7.9.8.10.12 Î S12,
one splits it after each descent: 6 | 3.11 | 1.4.5 | 2.7.9 | 8.10.12
then one reads it from right to left, and for each factor one creates the
associated tree where the root is the maximum and each node has only a right
child.
One gets then fives trees (12,10,8), (9,7,2), (5,4,1), (11,3) and (6).
And finally one tries to create the associated binary search tree, which is
possible if and only if t is sorted. What is more, by noting s
the word given by a ``lower reading'' of the final tree,
we get t= P(s).
With our example, we have t= P(6.11.3.12.9.5.4.1.7.2.10.8) is sorted.
4 Notations
The number of 23 1 patterns in a permutation s
is the number of pairs
(i,k) with i<k such that there exists j Î [i, k] with
s(k)<s(i)<s(j).
Note that the number of 23 1 patterns in a permutation s,
denoted below INV (s), is the number of inversions of
P(s).
For instance, the permutation s of
Fig. 1 has four 2 3 1 patterns (corresponding
to the pairs of letters (2,1), (3,1), (5,4) and (6,4)) and
P(s) has four inversions (given by the same pairs of letters).
For s Î Sn, we define z(s) by the largest l such that
n occurs before n-1 and n-1 occurs
before n-2 and ··· and
n-(l -2) occurs before n-(l-1)}.
For instance, z(519268374)=3.
For m,n ³ 0, we define the sets Sm,n
and Sm,n by
| Sm,n = { s Î Sm+n : z(s) ³ n }
and
|
|
m,n = { s Î Sm+n : z(s)
= n }. |
Let s Î Sm,n
and s=sL m sR, we note m' the largest letter of sR,
so we have the factorisation s=A m' B. It is this factorisation which
allowed the author to find equations verified by the generating functions.
We will use the usual notations [n]=1+q+... + qn-1=1-qn/1-q
and [n]!=[1][2] ··· [n]. Let C be a set of
permutations. By the ordinary (resp. exponential) generating function of C we mean the series
| C(x,y)= |
|
cm,nxmyn,
resp. |
C(x,y)= |
|
cm,n |
|
yn, |
| C(x,y;q)= |
|
cm,nxmyn,
resp. |
C(x,y;q)= |
|
cm,n |
|
yn, |
5 Functional Equations
Proposition 1
The Eulerian INV-generating function A(x,y;q) for general permutations is completely characterised by the
initial condition A(0,y;q)=1/(1-y) and the equation
| A(x,y;q)- A(xq,y;q) |
|
| x(1-q) |
|
= |
[ |
1+y A(xq,y;q) |
] |
|
. |
Proposition 2
The ordinary generating function B(x,y) for one-stack sortable permutations
is completely characterised by the equation
Proposition 3
The ordinary INV-generating function C(x,y) for two-stack
sortable permutations is completely characterised by the equation
| C (x,y;q) = |
|
+ x |
[ |
1+y C(xq,y;q) |
] |
|
. |
Proposition 4
The Eulerian inv-generating function D(x,y;q) for sorted
permutations is completely characterised
by the initial condition
D(0,y;q)=1/(1-y) and the equation
| D(x,y;q)- D(xq,y;q) |
|
| x(1-q) |
|
=(1-y) |
[ |
1+y
D(xq,y;q) |
] |
|
.
|
|
(x,y) =(1-y) |
[ |
1+yD(x,y) |
] |
|
. |
Proposition 5
The ordinary inv-generating function E(x,y;q) for sorted and
sortable permutations is completely characterised by the equation
| E (x,y;q) = |
|
+ x(1-y) |
[ |
1+y E(xq,y;q) |
] |
|
. |
Remarks
The ordinary length generating function B(x,0) for
one-stack sortable permutations can be solved by the kernel method.
The equations of Propositions 3 (two-stack sortable permutations)
and 5 (sorted and sortable permutations) can be solved when q=1 via the so-called
quadratic method, which is due to Brown [6, section 2.9.1].
There is no known q-analogue of this method!
On the other hand, the equations for the general permutations and for
sorted permutations can be ``solved'' as we will see in the next section.
6 Solving Equations with a q-Derivative
Both equations are of the following form:
|
|
|
(x,y) =c(y) |
[ |
1+yF(x,y) |
] |
|
,
(1) |
One uses the two following results in order to ``solve'' these equations.
Lemma 1 [Bernoulli linearisation]
Let F(x,y) Î R(y)[[x]] be defined by the initial condition
F(0,y)=1/(1-y) and Eq. (
1)
, with c(y)=1 or
c(y)=1-y. Let G(x,y) be
the following series of R(y)[[x]]:
Then G(0,y)=(1-y)/c(y) and
| y |
|
(x,y)-c(y) |
[ |
1+yF(x,0) |
] |
G(x,y)+1=0. |
polynomial coefficients
in y, i.e.,
G(x,y) Î R[y][[x]].
Lemma 2 [Laplace transform]
Let h(x,y) Î R[y][[x]] be a formal series in x with polynomial
coefficients in y. Let G(x,y) be the series of R(y)[[x]]
defined by an initial condition G(0,y) Î R(y) and the
differential equation:
| y |
|
(x,y)- |
[ |
1+yh(x,y) |
] |
G(x,y)+1=0. |
| H(x,y) = exp |
é
ê
ê
ê
ê
ë |
- |
ó
õ |
|
h(u,y) d u |
ù
ú
ú
ú
ú
û |
= |
|
Hi(y) |
|
. |
|
|
ó
õ |
|
e-u/yH(u,y) d u =G(0,y). |
For general permutations, with c(y)=1, one gets
For sorted permutations, with c(y)=1-y,
the series F(x,y) is the exponential generating function D(x,y) for
sorted permutations.
The series G(x,y)=1/[ (1-y) (1+yD(x,y))] satisfies (1)
with h(x,y)=(1-y)D(x,0)-1. Moreover, G(0,y)=1.
With the notations of Lemma 2, we have:
H(x,y)=exp(x+(y-1) D (x))
where Lemma 2 gives
the following result.
Proposition 6 Let
where dm,0 is the number of sorted
permutations of length m. Then the series D(x) is
completely characterised by the following equation:
|
|
ó
õ |
|
e-u(1-y)/y exp |
[ |
(y-1) D
(u) |
] |
du = 1-y. |
|
æ
ç
ç
è |
|
|
, y |
ö
÷
÷
ø |
= 1-y, or, equivalently |
|
|
æ
ç
ç
è |
u, |
|
|
ö
÷
÷
ø |
= |
|
. |
The first coefficients of the series are
1,1,2,5,17,68,326,1780,11033,76028,578290,4803696.
One does not know if this series is algebraic, D-finite,...Thus, the generating function for sorted permutations remains mysterious.
Mireille Bousquet-Mélou will give a solving method
for the full q-analogue equations in a for coming paper.
References
- [1]
-
Barcucci (Elena), Del Lungo (Alberto), Lanini (S.), Macrí (M.), and
Pinzani (Renzo). --
The inversion number of some permutations with forbidden
subsequences. Proceedings of SOCA'96 Tianjin, 1996,
pp. 21--32.
- [2]
-
Bousquet-Mélou (Mireille). --
A method for the enumeration of various classes of column-convex
polygons. Discrete Mathematics, vol. 154, n°1-3,
1996, pp. 1--25.
- [3]
-
Bousquet-Mélou (Mireille). --
Multi-statistic enumeration of two-stack sortable permutations. Electronic Journal of Combinatorics, vol. 5, n°1, 1998.
- [4]
-
Bousquet-Mélou (Mireille). --
Sorted and/or sortable permutation. Preprint, LaBRI,
1998.
- [5]
-
Brown (William G.). --
Enumeration of quadrangular dissections of the disk. Canadian
Journal of Mathematics, vol. 17, 1965, pp. 302--317.
- [6]
-
Brown (William G.). --
On the existence of square roots in certain rings of power series.
Mathematische Annalen, vol. 158, 1965, pp. 82--89.
- [7]
-
Brown (William G.). --
On the enumeration of non-planar maps. Memoirs of the American
Mathematical Society, vol. 65, 1966, p. 42.
- [8]
-
Brown (William G.) and Tutte (William Thomas). --
On the enumeration of rooted non-separable planar maps. Canadian
Journal of Mathematics, vol. 16, 1964, pp. 572--577.
- [9]
-
Cori (Robert), Jacquard (B.), and Schaeffer (Gilles). --
Description trees for some families of planar maps. In Formal
Power Series and Algebraic Combinatorics, pp. 196--208. --
1997. Proceedings of the 9th Conference, Vienna.
- [10]
-
Cori (Robert) and Richard (Jean). --
Énumération des graphes planaires à l'aide des séries
formelles en variables non commutatives. Discrete Mathematics, vol. 2,
1972, pp. 115--162.
- [11]
-
Dulucq (Serge), Gire (S.), and West (Julian). --
Permutations with forbidden subsequences and nonseparable planar
maps. Discrete Mathematics, vol. 153, n°1-3, 1996,
pp. 85--103.
- [12]
-
Knuth (Donald E.). --
The Art of Computer Programming. --
Addison-Wesley, 1973, vol. 1.
- [13]
-
Rawlings (Don). --
The Euler-Catalan identity. European Journal of
Combinatorics, vol. 9, n°1, 1988, pp. 53--60.
- [14]
-
West (Julian). --
Permutations with restricted subsequences and stack-sortable
permutations. --
PhD thesis, MIT, 1990.
- [15]
-
Zeilberger (Doron). --
A proof of Julian West's conjecture that the number of
two-stack-sortable permutations of length n is 2(3n)!/((n+1)!(2n+1)!).
Discrete Mathematics, vol. 102, n°1, 1992,
pp. 85--93.
This document was translated from LATEX by
HEVEA.