



Next: Application
Up: Épisode second : un peu
Previous: Le symbole de Legendre
On trouvera dans [Naudin] une approche du symbole de Jacobi par Zolotarev
basée sur la signature d'une permutation.
Nous utiliserons la définition classique.
On prolonge le symbole de Legendre par 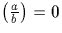 si a est un multiple
de b.
Pour
si a est un multiple
de b.
Pour 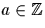 et b entier impair, on définit le symbole de Jacobi par
et b entier impair, on définit le symbole de Jacobi par
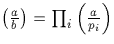 avec
avec 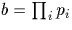 décomposition de b en
facteurs premiers.On peut d'ores et déjà remarquer que
décomposition de b en
facteurs premiers.On peut d'ores et déjà remarquer que 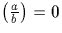 si
et seulement si a et b ne sont pas étrangers.
si
et seulement si a et b ne sont pas étrangers.
Ainsi, si a est un carré modulo b (b étant étranger avec a)
alors 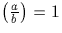 . On remarquera aussi que
. On remarquera aussi que 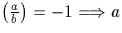 est non carré modulo b
mais qu'on peut avoir
est non carré modulo b
mais qu'on peut avoir 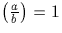 sans que a soit un carré modulo b.
Exemple :
sans que a soit un carré modulo b.
Exemple : 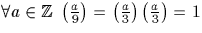 , or a=5 n'est
pas un carré dans
, or a=5 n'est
pas un carré dans  . Il est facile de voir que le symbole de Jacobi est un symbole totalement
bimultiplicatif : il est totalement multiplicatif en sa première variable car
. Il est facile de voir que le symbole de Jacobi est un symbole totalement
bimultiplicatif : il est totalement multiplicatif en sa première variable car
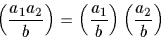
et il est totalement multiplicatif en sa deuxième variable car
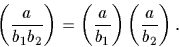
Par conséquent, la loi de réciprocité, une fois démontrée pour
le symbole de Legendre (ce que nous ferons dans le chapitre
suivant), vaut aussi pour le symbole de Jacobi ;
on obtient la loi de réciprocité généralisée :
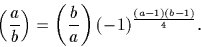
La multiplicativité du symbole de Jacobi en fait un caractère
réel, on a vu l'importance de cette notion au §




Next: Application
Up: Épisode second : un peu
Previous: Le symbole de Legendre
Cyril Banderier
7/23/1997
![]()
![]()
![]()