



Next: Nanobiographies
Up: Pour quelques réciprocités de
Previous: Loi de réciprocité octale
Les plus courtes étant souvent les meilleures, voici une preuve ``exprès''
de la loi de réciprocité pour le symbole de Legendre, d'après
G. Rousseau dans On the quadratic reciprocity law, Australian Mathematical
Society, 3 (1991) :
considérons le groupe quotient multiplicatif
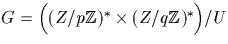 ,où
,où 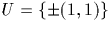 . Le produit m de tous les éléments de G est
. Le produit m de tous les éléments de G est
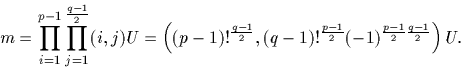
D'après le théorème chinois, m est aussi égal à
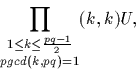
donc, d'après le critère d'Euler,
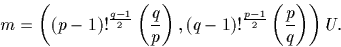
La loi s'obtient en comparant les expressions pour m.
Des preuves encore plus élémentaire ont été données, cf. J.S. Frame
[Amer. Math. Monthly 85
(1978), 10, 818-819], mais la
preuve précédente est l'une des plus simples à retenir.
La loi de réciprocité et la formule 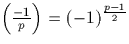 (un cas spécial du critère d'Euler) sont facilement étendues par
multiplicativité au symbole de Jacobi pour tous p,q>1 impairs.
(un cas spécial du critère d'Euler) sont facilement étendues par
multiplicativité au symbole de Jacobi pour tous p,q>1 impairs.
La loi complémentaire pour 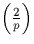 peut être simplement déduite du
théorème :
on écrit p=4k+e avec
peut être simplement déduite du
théorème :
on écrit p=4k+e avec 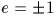 ,
, 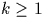 .Remarquons alors que a=(p+e)/2 est impair donc
.Remarquons alors que a=(p+e)/2 est impair donc
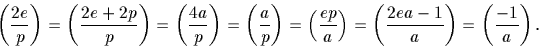
Ainsi
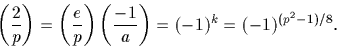
Auteur : Cyril Banderier, 23 juillet 1997.
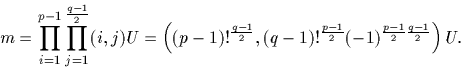
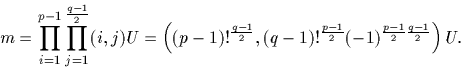
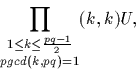
![]()
![]() (un cas spécial du critère d'Euler) sont facilement étendues par
multiplicativité au symbole de Jacobi pour tous p,q>1 impairs.
(un cas spécial du critère d'Euler) sont facilement étendues par
multiplicativité au symbole de Jacobi pour tous p,q>1 impairs.
![]() peut être simplement déduite du
théorème :
on écrit p=4k+e avec
peut être simplement déduite du
théorème :
on écrit p=4k+e avec ![]() ,
, ![]() .Remarquons alors que a=(p+e)/2 est impair donc
.Remarquons alors que a=(p+e)/2 est impair donc
![]()
![]()