



Next: Réciprocité et nombres premiers
Up: Réciprocité et tests de
Previous: Critère de Pépin sur
Si, pour x non multiple de p, ![$x^{p-1}\not \equiv 1 \ [p]$](img274.gif) , alors p n'est
pas premier (contraposée du petit théorème de Fermat).
On a la ``réciproque '' : si
, alors p n'est
pas premier (contraposée du petit théorème de Fermat).
On a la ``réciproque '' : si
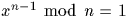 et
et 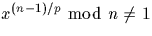 pour tout facteur premier p de n-1 alors n est premier.
C'est la base même du test de primalité par descente-remontée
(ou downrun) dont voici un exemple tiré de [Knuth] :
pour tout facteur premier p de n-1 alors n est premier.
C'est la base même du test de primalité par descente-remontée
(ou downrun) dont voici un exemple tiré de [Knuth] :
n0=37866809061660057264219253397 ;
puisque 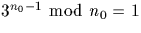 ,
n0 est sûrement premier.
,
n0 est sûrement premier.
n0-1=2.2.19.107.353.n1 avec n1=13191270754108226049301 ;
puisque
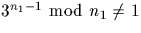 , n1 est composé.
, n1 est composé.
En effet n1=91813.n2 où n2=143675413657196977 ;
puisque
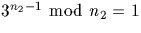 , n2 est sûrement premier.
, n2 est sûrement premier.
n2-1=24.32.547.n3 et n3=1103.n4 où n4=1653701519 ;
puisque 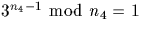 , n4 est sûrement premier.
, n4 est sûrement premier.
n4-1=2.7.19.23.137.1973 est complètement factorisé donc on peut
commencer notre test :
| x |
p |
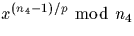 |
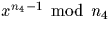 |
| 2 |
2 |
1 |
1 |
| 2 |
7 |
766408626 |
1 |
| 2 |
19 |
332952683 |
1 |
| 2 |
23 |
1154237810 |
1 |
| 2 |
137 |
373782186 |
1 |
| 2 |
1973 |
490790919 |
1 |
| 3 |
2 |
1 |
1 |
| 5 |
2 |
1 |
1 |
| 7 |
2 |
1653701518 |
1 |
Pour p=2, on a essayé x=2, 3, 5 avant de trouver x=7 pour
conclure. Donc n4 est premier d'où n2 est complètement factorisé.
Et ainsi, en faisant un tableau similaire pour n0 (car on a complètement
factorisé n0-1), on obtient que n0 est premier. Mais bien sûr, on
peut encore gagner du temps en utilisant la loi de réciprocité quadratique
qui nous aurait indiqué, par le simple calcul de n4 mod 10,
que 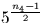 mod n4=1.
mod n4=1.




Next: Réciprocité et nombres premiers
Up: Réciprocité et tests de
Previous: Critère de Pépin sur
Cyril Banderier
7/23/1997
![]() mod n4=1.
mod n4=1.