



Next: In fine
Up: Quod erat demanstrandum
Previous: Secundo
Cette démonstration est aussi celle qui figure dans La loi de
réciprocité quadratique, Revue de Mathématiques Spéciales,
mars 1990 par P. Delezoide. Ce dernier en profite d'ailleurs pour faire quelques
remarques d'ordre géométrique qui figurent également dans [Hardy].
On note 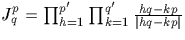 .Notons que Jpq est bien défini puisque pour tout
.Notons que Jpq est bien défini puisque pour tout 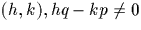 .
Fixons k. Alors dire que
.
Fixons k. Alors dire que 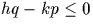 revient à
dire
revient à
dire 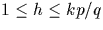 . Il y a donc E(kp/q) valeurs de h pour lesquelles
. Il y a donc E(kp/q) valeurs de h pour lesquelles
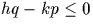 . Ainsi
. Ainsi 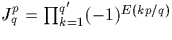 .En passant modulo 2 la relation du primo, on obtient
.En passant modulo 2 la relation du primo, on obtient
![$k \equiv E(kp/q)+e_k+r_k\ [2]$](img183.gif) .Donc
.Donc 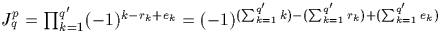 .Or
.Or 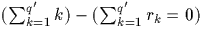 d'après le secundo.
Il en résulte
d'après le secundo.
Il en résulte 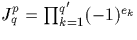 . La
relation du primo donne
. La
relation du primo donne ![$kp \equiv (-1)^{e_k} r_k\ [q]$](img187.gif) .Donc
.Donc ![$J^p_q \equiv \prod^{q'}_{k=1} \frac{kp}{r_k}
\underbrace{\equiv}_{secundo} p^{q'} \equiv \left(\frac{p}{q}\right)\ [q]$](img188.gif) .Comme
.Comme 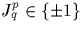 , on a bien
, on a bien 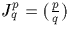 .
.
Cyril Banderier
7/23/1997
![$J^p_q \equiv \prod^{q'}_{k=1} \frac{kp}{r_k}
\underbrace{\equiv}_{secundo} p^{q'} \equiv \left(\frac{p}{q}\right)\ [q]$](img188.gif) .Comme
.Comme