PSyHCoS: Parameter Synthesis for Hierarchical Concurrent Systems

Screenshots

Simulator

Simulator

Verification window

Verification window and editor

New! The slides of the CAV 2013 presentation are now available here.

PSyHCoS [ALSDL13] is a tool that groups techniques of parameter synthesis for Parametric Stateful Timed CSP (in short: PSTCSP). PSTCSP is the modeling language of PSyHCoS.

In particular, PSyHCoS implements the inverse method initially defined in the setting of timed automata in [ACEF09], and extended for PSTCSP [ALSD12], as well as further model checking algorithms.

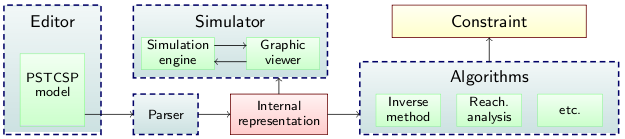
Architecture of PSyHCoS
Architecture of PSyHCoS

Features

PSyHCoS comes with:

Among the verification and synthesis algorithms, PSyHCoS features:

Download and Install

PSyHCoS can be executed under Windows. It has been tested under Windows XP and 7 (natively) using a 32 bits architecture. Note that you need a .NET framework installed, that can be downloaded for free from the Microsoft Web site; PSyHCoS has been developed and tested using the 3.5 .NET framework, but it may work for other versions as well.

PSyHCoS can also be executed under Linux and Mac (using, e.g., Mono).

Note that the binary will probably not work properly on 64 bits systems. If you meet an "unknown parsing error", please switch to a 32 bits system. (This comes from the polyhedra.dll file; we are currently working on a 64 bits version of this DLL.)

In case you meet any problem when executing (or compiling) PSyHCoS, please contact us, and we will do our best to help you.

Download

Run

On Windows (we tested the tool on XP, 7 and 8), download the binaries, unzip the file, and simply run the binary Psyhcos.exe. Make sure a .NET framework is installed.

On other platforms, first install mono, download the binaries, unzip the file, and then simply run the binary Psyhcos.exe.

Compile

There is no particular need to compile PSyHCoS, since we provide binaries for all platforms. However, if you wish to modify PSyHCoS’ code, you will have to compile it.

Since PSyHCoS is developed in a .NET framework, it can be only compiled (as far as we know) in a Microsoft Visual Studio environment. We provide the MVS project file (PSyHCoS.sln), so you only need to open it and compile.

The constraint solving engine partially relies on the Parma Polyhedra Library.
PSyHCoS is distributed under the GNU General Public License.

User Manual

Download the user manual, that also summarizes PSyHCoS’ features and internal architecture.

It contains a brief introduction to the tool, presents the input syntax for PSTCSP (and its extensions allowed by PSyHCoS), and describes commands for verification and parameter synthesis.

Experiments

We give below a list of experiments; some of them are related to the paper [ALSD12]. For all experiments, we give the PSyHCoS sources and binaries, the models, and the experiments data.

Description of the models

Mex

Mex is a sample PSTCSP model mentioned in [ALSD12], adapted from Example 2 in [SLDZ09].
We consider the following reference parameter valuation:
u1 = 1, u2 = 2

Mex’

Mex’ is the same model as Mex, but with a different reference parameter valuation.
u1 = 2, u2 = 1

Bridge

This case study refers to the bridge crossing puzzle. The following description is borrowed from this Web page.

The sun has set as the King, the Queen, the Knight and the Lady arrive at the bridge right outside the castle walls. They have just returned from a long and dangerous trip across the realm. Scouts have spotted the King’s arch enemy closing in on the castle. It is estimated that the King’s foe will arrive accompanied by merciless troops in 17 minutes. That means that all four member of our Royal party must cross the bridge and rest safely together on the bridge’s other side before disaster strikes!

It’s not as easy as it seems. Only two people can cross the bridge at once (it’s not as sturdy as it used to be) and those crossing the bridge must carry the torch (so that they can see!). The torch can’t be thrown across the bridge… it’s windy tonight and the torch would probably blow out… leaving our Royal friends to stumble in the dark.

To make matters worse each person takes a different amount of time to cross the bridge. If two people cross the bridge together it will take them the longer of the two travel times to cross. In other words, the Knight can cross the bridge in one minute, but the Queen requires ten minutes. Therefore, if the Knight and Queen cross the bridge together a precious ten minutes will have past.

Our parametrization of this problem was performed by considering that the time in which they must cross the bridge is constant and known (viz., 17 minutes), whereas the amount of time needed by each of the 4 characters is unkown, hence parametric. As a consequence, our constraint guarantees that, for any valuation (including real-valued) satisfying the constraint output by our method, the four persons will be safe in at most 17 minutes.

Hence, we consider the following reference parameter valuation, conform to the original non-parametric model:
KNIGHT = 1, LADY = 2, KING = 5, QUEEN = 10

Fischer

This case study refers to the Fischer mutual exclusion protocol, as described in [ALSD12].
Fischeri has i protocols in parallel.
We consider the following reference parameter valuation:
epsilon = 3, delta = 4

Jobshop

This case study refers to a tentative translation into PSTCSP of the jobshop scheduling problem with 2 jobs and 4 tasks of [AM01], and that we converted to PSTCSP.
We consider the following reference parameter valuation:
d11 = 3, d12 = 6, d13 = 1, d14 = 7, d21 = 10, d22 = 8, d23 = 5, d24 = 4

RCS

This case study is a parameterized version of the railway control system from the STCSP module of PAT. The following description is borrowed from this Web page.

This system automatically controls trains passing a critical point such as a bridge. It uses a computer to guide trains from several tracks crossing a single bridge instead of building many bridges. Obviously, a safety-property of such a system is to avoid the situation where more than one train is crossing the bridge at the same time. Our model consists of three components: a train, a gate and a controller. The gate is lowered to allow trains to cross the bridge and up when there is no train crossing the bridge. The controller monitors the approaching of a train, and instructs the gate to be lowered within the appropriate time. The train is modeled abstractly with nearing, entering and leaving behaviors.

RCSi has i trains.
We consider the following reference parameter valuation, conform to the original non-parametric model:
Wait11 = 11, Wait10 = 10, Wait4 = 4, Wait1 = 1

TrainAHV

This case study is a tentative translation into PSTCSP of the train example from [AHV93].
It consists of a train, a gate and a controller. Of course, the train should not cross when the gate is not closed.
We consider the following reference parameter valuation:
a = 4, b = 6, c = 1, d = 2, e = 2, f = 3

Experiment results

All experiments were performed on a Windows XP machine with an Intel Quad Core 2.4 GHz processor with 4 GiB memory. |U|, |S|, |T|, |X|, t represent the number of parameters, the number of states, the number of transitions, the maximum number of clocks used, and the computation time in seconds, respectively.

The model in the PSTCSP syntax is available by clicking on a case study name. The exact output as given by PSyHCoS for each experiment is available by clicking on "log".

Deadlock-freeness was checked using the optimization mentioned in [ALSD12], viz., the same as in ReachAll+ and IM+.

Model reachAll reachAll+ Deadlock-freeness IM IM+
|U| |S| |T| |X| t log |S| |T| |X| t log Valid? t log |S| |T| |X| t log |S| |T| |X| t log
Mex 2 8 14 2 0.008 log 8 14 2 0.006 log Yes 0.054 log 3 5 2 0.004 log 3 5 2 0.005 log
Mex’ 2 8 14 2 0.008 log 8 14 2 0.006 log Yes 0.054 log 8 14 2 0.016 log 8 14 2 0.008 log
Bridge 4 − − − M.O. − − − − M.O. − − M.O. − 2799 5459 2 253 log 2799 5459 2 455 log
Fischer2 2 − − − M.O. − − − − M.O. − − M.O. − 44 75 2 0.086 log 45 77 2 0.103 log
Fischer3 2 − − − M.O. − − − − M.O. − − M.O. − 870 2004 3 3.38 log 313 730 3 0.723 log
Fischer4 2 − − − M.O. − − − − M.O. − − M.O. − 11081 31452 4 41.9 log 1987 5781 4 8.65 log
Fischer5 2 − − − M.O. − − − − M.O. − − M.O. − 133363 447473 5 1176 log 12689 43801 5 84.5 log
Fischer6 2 − − − M.O. − − − − M.O. − − M.O. − − − − M.O. − 86058 342178 6 1144 log
Jobshop 8 13578 20262 2 21.0 log 11872 17387 2 18.1 log No 0.068 log 1112 1902 2 17.1 log 877 1497 2 22.8 log
RCS2 4 52 64 4 0.038 log 52 64 4 0.059 log Yes 0.110 log 52 64 4 0.091 log 52 64 4 0.147 log
RCS3 4 233 296 4 0.186 log 233 296 4 0.300 log Yes 0.359 log 233 296 4 0.310 log 233 296 4 0.513 log
RCS4 4 1070 1374 4 1.74 log 1070 1374 4 1.58 log Yes 1.77 log 1070 1374 4 1.40 log 1070 1374 4 2.38 log
RCS5 4 5567 7172 4 10.5 log 5567 7172 4 9.54 log Yes 9.00 log 5567 7172 4 7.83 log 5567 7172 4 16.7 log
RCS6 4 33716 43472 4 91.7 log 33716 43472 4 54.5 log Yes 56.3 log 33716 43472 4 60.4 log 33716 43472 4 91.3 log
TrAHV 7 7216 13361 6 14.2 log 7216 13361 6 15.8 log Yes 16.2 log 227 321 6 0.555 log 227 321 6 0.655 log

References

[ACEF09]
Étienne André, Thomas Chatain, Emmanuelle Encrenaz and Laurent Fribourg. An Inverse Method for Parametric Timed Automata. International Journal of Foundations of Computer Science 20(5), pages 819–836, 2009. Flag United Kingdom [PDF (published version) | PDF (author version) | BibTeX]
[AHV93]
Rajeev Alur, Thomas A. Henzinger and Moshe Y. Vardi. Parametric real-time reasoning. In STOC’93, pages 592–601. ACM, 1993.
[ALSD12]
Étienne André, Liu Yang, Sun Jun and Dong Jin Song. Parameter Synthesis for Hierarchical Concurrent Real-Time Systems. In Karin Breitman, Isabelle Perseil, Marc Pouzet (eds.), ICECCS’12, IEEE Computer Society, pages 253–262, July 2012. Flag United Kingdom [PDF (author version) | PDF (long author version) | BibTeX]
[ALSDL13]
Étienne André, Liu Yang (刘杨), Sun Jun, Dong Jin Song and Lin Shang-Wei (林尚威). PSyHCoS: Parameter Synthesis for Hierarchical Concurrent Real-Time Systems. In Natasha Sharygina and Helmut Veith (eds.), CAV’13, LNCS 8044, Springer, pages 984–989, July 2013. Acceptance rate: 33%. (English) [PDF (author version) | BibTeX | Slides]
[AM01]
Yasmina Abdeddaïm and Oded Maler. Job-shop scheduling using timed automata. In CAV’01, volume 2102 of LNCS, pages 478–492. Springer Berlin / Heidelberg, 2001.
[SLDZ09]
Jun Sun, Yang Liu, Jin-Song Dong, and Xian Zhang. Verifying Stateful Timed CSP using implicit clocks and zone abstraction. In ICFEM’09, volume 5885 of LNCS, pages 581–600. Springer, 2009.

Contact

This page makes use of valid HTML 5 and valid CSS.

Content and CSS can be reused and modified under the terms of license Creative Commons Attribution 3.0 Unported (CC BY 3.0).

Creative Commons Attribution 3.0 Unported