Table des matières
Semana 11: Funciones de activación y de pérdida en Pytorch
25 de agosto del 2020
Notas realizadas por Jorge García Flores sobre el curso/cover que Iván Vladimir Meza hizo sobre un tema original de Yann LeCun y Alfredo Canziani en la primavera-verano del 2020
I. Funciones de activación
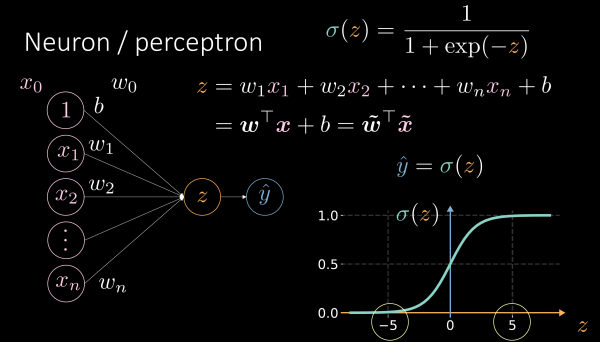
Repaso: ¿Qué es una función de activación?
Función no lineal que nos permite transformar una suma de puntajes con pesos en una “neurona”

Fuente: Diapositivas 00 - Logic neurons.pdf de Alfredo Canziani
Rectificadores
- Función rectificadora (ReLU)
- Rectificador aleatorio (RReLU)
- Rectificador permeable (Leaky ReLU)
Características:
- Poco sensibles a la escala (“puedes multiplicar la señal por 2 y la salida refleja exactamente la multipicación por 2: la escala no cambia el comportamiento de la función”)
- Sirven para redes con pocas capas (“skinny networks”)
PReLU
El valor negativo se multiplica por un parámetro a que se puede aprender
"La a puede variar de acuerdo a cada canal de entrada"
Softplus
Aproximación derivable de ReLU.
Repaso: sobre derivabilidad (“sin derivabilidad no hay gradiente”)
"la identidad para los valores positivos y asintóticamente cero para los valores negativos"
- Esta función es más sensible a la escala que las funciones quebradas (de la familia ReLU). Aplicar una escala (por ejemplo, a nivel de una capa) puede modific el comportamiento de la salida.
ELU
"El algoritmo de gradiente puede converger más rápido con puntajes positivos y negativos con respecto a arquitecturas con puros puntajes positivos"
"Los valores negativos permiten que el promedio sea , lo cual puede hacer que el algoritmo de gradiente converja más rápido"
Función sigmoide
"Si acumulas las capas de sigmoides en tu red. ésta no va a aprender de manera eficiente [...] en este caso debes poner mucha atención a la normalización"
"Para redes muy profundas, las funciones no lineales quebradas [como el rectificador] son más convenientes"
Softsign
"Un problema con la tangente hiperbólica o la función sigmoide es que cuando te acercas a la asíntota, el gradiente se va a 0 demasiado rápido y si los pesos de una determinada neurona son muy grandes, la saturan... el valor del gradiente se desploma y la neurona no aprende rápido... Softsign intenta resolver este problema."
Función de umbral
"No se puede propagar gradiente ahí: por culpa de esta función no se inventó la retropropagación en la década de 1960 o incluso 1970"
Hardshrink
Rara vez utilizada, salvo en el marco de sparse coding (aquí una definición y acá un artículo de divulgación) al respecto.
- ¿Se puede definir sparse coding como la “activación de una cantidad mínima de neuronas”?
Preguntas y respuestas
- ¿Qué es el polinomio de Chebyshev?"funciones no lineales parametrizables con polinomios de Chebyshev para aproximar bien la función"
- En un marco de aprendizaje profundo geométrico, el polinomio de Chebysev, se puede usar para aproximar una función cuya complejidad representa un obstáculo para su cálculo. - ¿Qué son los spring parameters?
- Funciones monótonas (o isótonas)
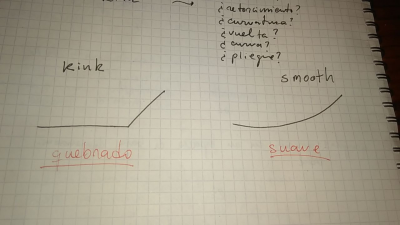
- Momento lexicográfico: ¿cómo traducimos kink?
- Softmax y temperatura (en el marco de aprendizaje reforzado)
II. Funciones de pérdida
Función de pérdida L1
- Valor absoluto de la diferencia entre el valor obtenido y el valor objetivo (o deseado)
Función de verosimilitud negativa
- Balanceando juegos de datos desbalanceados con Yann:
Pérdida por entropía cruzada
- Repaso de la función de entropía cruzada
- Sobre la divergencia Kullback-Leibler
### Perdida binaria por entropía cruzada
Pérdida por divergencia KL
Pérdida por inmersión de coseno (*CosineEmbeddingLoss*)
- Repaso de la similaridad por coseno